Симметричные рисунки по геометрии: Что такое осевая и центральная симметрия?
Что такое осевая и центральная симметрия?
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
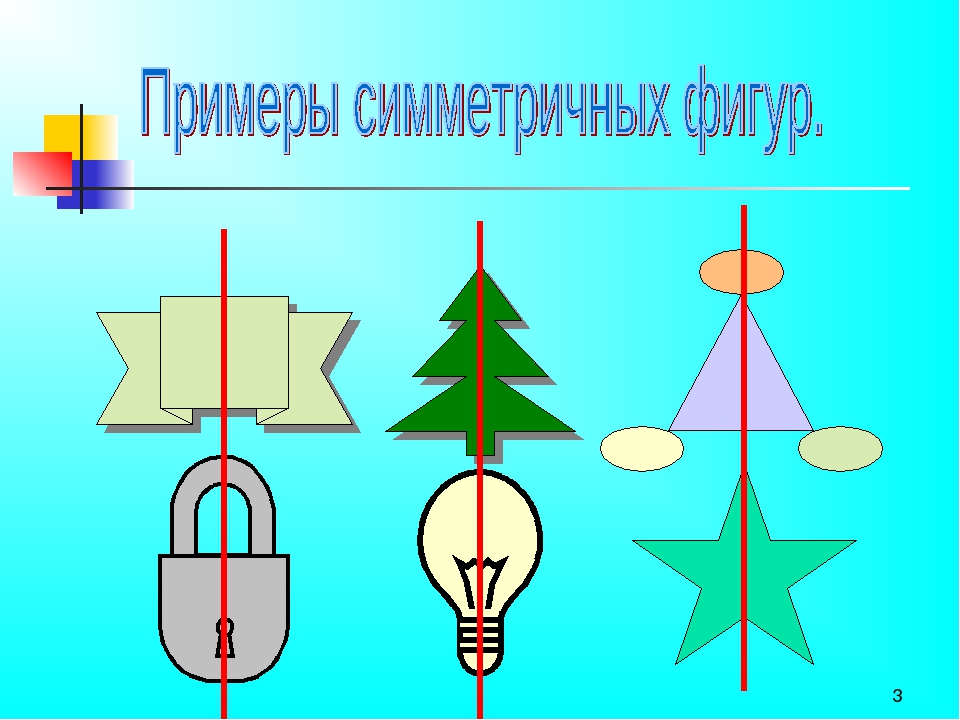
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, у которых есть ось и центр симметрии.
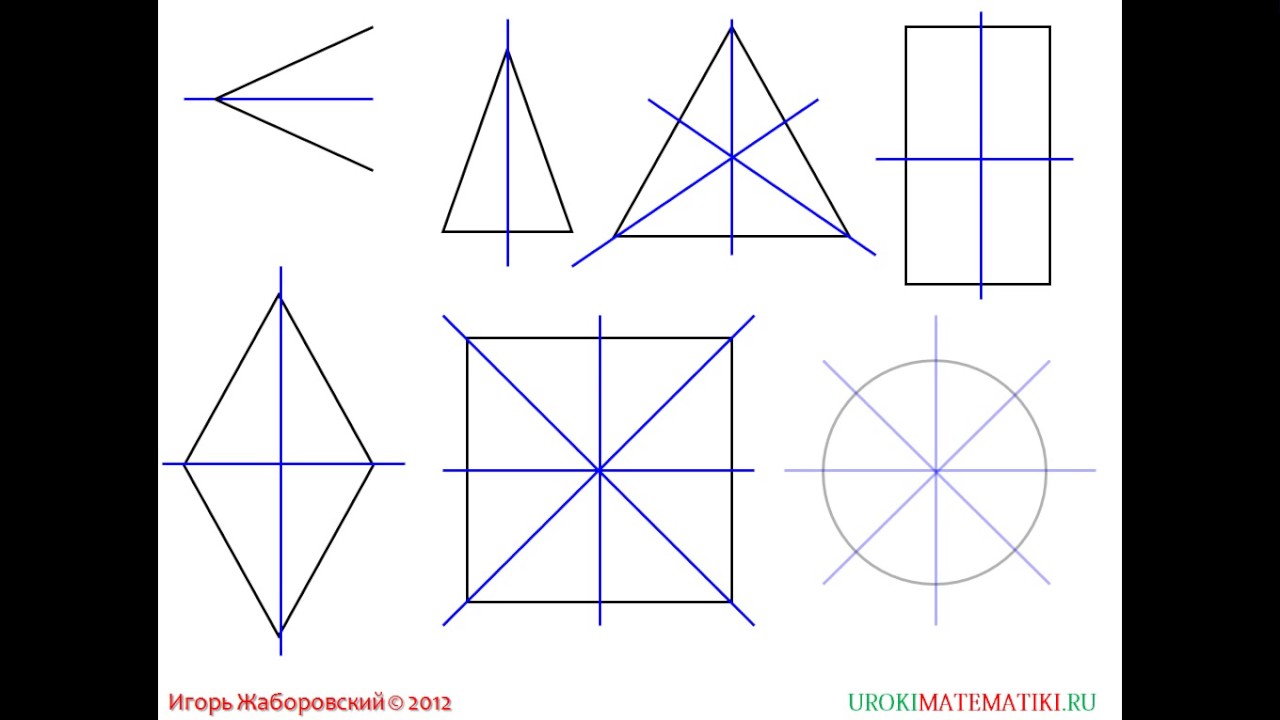
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник и ромб.

- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Не зря осевую и центральную симметрию изучают в 8 классе — цифра 8 очень симметрична. Если вы хотите, чтобы ваш ребенок чертил и высчитывал не хуже да Винчи, записывайтесь на бесплатный вводный урок математики.
Преподаватели школы Skysmart на интересных примерах из жизни объяснят любую тему, а на нашей интерактивной доске и сам Леонардо не отказался бы почертить.
Осевая симметрия
Вот, как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.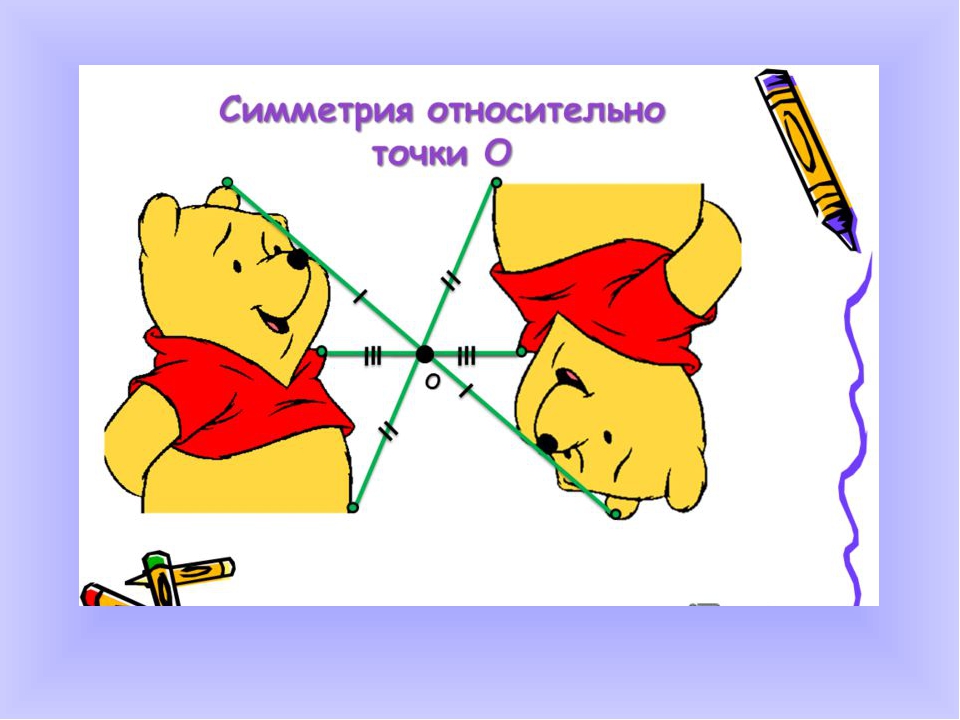
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
На рисунках осевая симметрия: точки A и B симметричны относительно прямой a; точки R и F симметричны относительно прямой A
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.

- Найдем расстояние от вершин треугольника ABC до точек на прямой.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника с осевой симметрией.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Измеряем расстояние от точки B до прямой l и от точки A до прямой l.

- Проводим прямую от точки А через прямую l, выводя за ось симметрии.
- Проводим прямую от точки B через прямую l, выводя за ось симметрии.
- Соединяем точки отрезка A1B1.
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
На картинках центральная симметрия: точка O здесь — центр симметрии
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.

- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Постройте треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки О).
- По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
- Выводим отрезки за точку О.
- Измеряем отрезки AO, BO, CO и чертим такие же на противоположной стороне.
- Получаем два центрально-симметричных треугольника.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.

- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки равные отрезкам АО и АB.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1 N1.
Докажите, что MN = М1 N1.
Подсказка: опустите перпендикуляры из точки N и N1 на прямую MМ1
Задачка 2. Постройте фигуру, симметричную данной относительно оси a.
Чтобы у вашего ребенка не возникало больше вопросов, как построить осевую симметрию или чем центральная симметрия отличается от зеркальной, — запишите его на уроки математики в онлайн-школу Skysmart. На наших занятиях даже самые скучные геометрические чертежи превращаются в забавные рисунки.
9 класс Конспект уроку — презентация по геометрия тема «Симметрия относительно прямой. Симметрия относительно точки»
Про матеріал
Учебно-познавательная деятельность учащихся Я привожу примеры фигур и их образов при геометрических перемещениях; фигур, которые имеют центр симметрии, ось симметрии. Могу объяснить, что такое: перемещение (движение) образ фигуры при геометрическом перемещении; фигура, симметричная данной относительно точки (прямой) симметрия относительно точки (прямой).
Перегляд файлу
Зміст слайдів
«Симметрия….. есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». математик Герман Вейль
Номер слайду 2
Учебно-познавательная деятельность учащихся Я привожу примеры фигур и их образов при геометрических перемещениях; фигур, которые имеют центр симметрии, ось симметрии.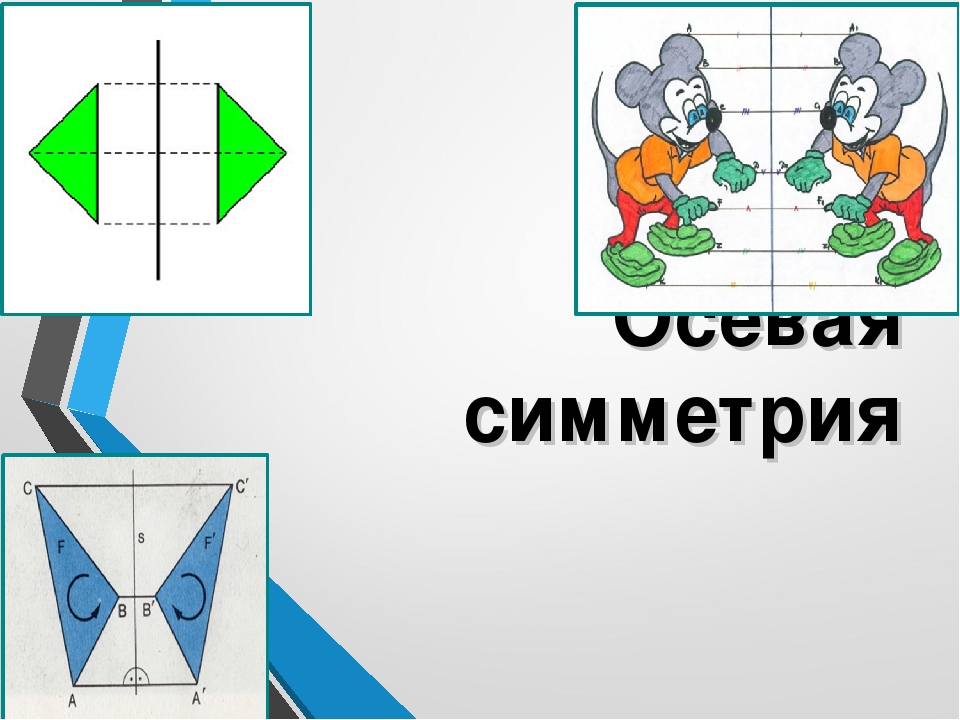 Могу объяснить, что такое: перемещение (движение) образ фигуры при геометрическом перемещении; фигура, симметричная данной относительно точки (прямой) симметрия относительно точки (прямой). Изображаю и нахожу на рисунках фигуры, в которые переходят данные фигуры при различных видах перемещений
Могу объяснить, что такое: перемещение (движение) образ фигуры при геометрическом перемещении; фигура, симметричная данной относительно точки (прямой) симметрия относительно точки (прямой). Изображаю и нахожу на рисунках фигуры, в которые переходят данные фигуры при различных видах перемещений
Номер слайду 3
Симметрия относительно точки. Симметрия относительно прямой.
Номер слайду 4
Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства.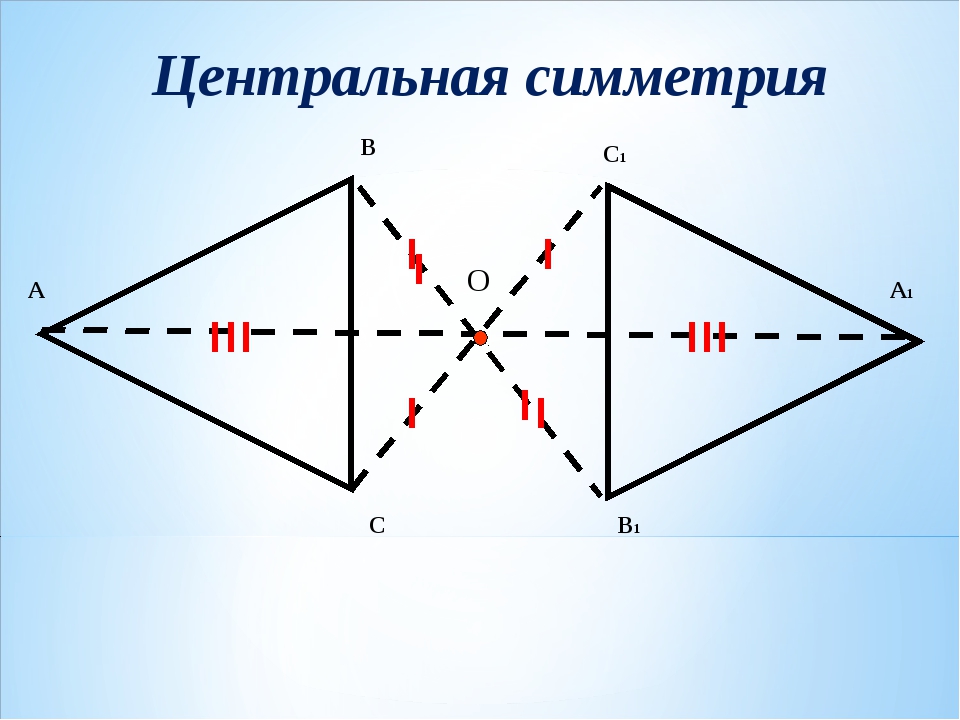
Номер слайду 5
https://bubbl.us/10421196
Номер слайду 6
Сколько осей симметрии имеет каждая из фигур? Как расположены оси симметрии фигуры, если их больше двух?Какая фигура самая симметричная?Какая фигура «несимметричная»?
Номер слайду 7
Сколько осей симметрии имеет каждая из фигур? Как расположены оси симметрии фигуры, если их больше двух?Какая фигура самая симметричная?Какая фигура «несимметричная»?
Номер слайду 8
Что общего у данных фигур?123465
Номер слайду 9
Какая из фигур, приведенных на рисунке лишняя?
Номер слайду 10
Симметрия относительно прямой – осевая симметрия
Номер слайду 11
Свойства симметрия Для любой точки плоскости всегда можно построить симметричную ей точку относительно некоторой прямой Отрезок, соединяющий симметричные точки, перпедикулярен оси симметрии и делится ею пополамl.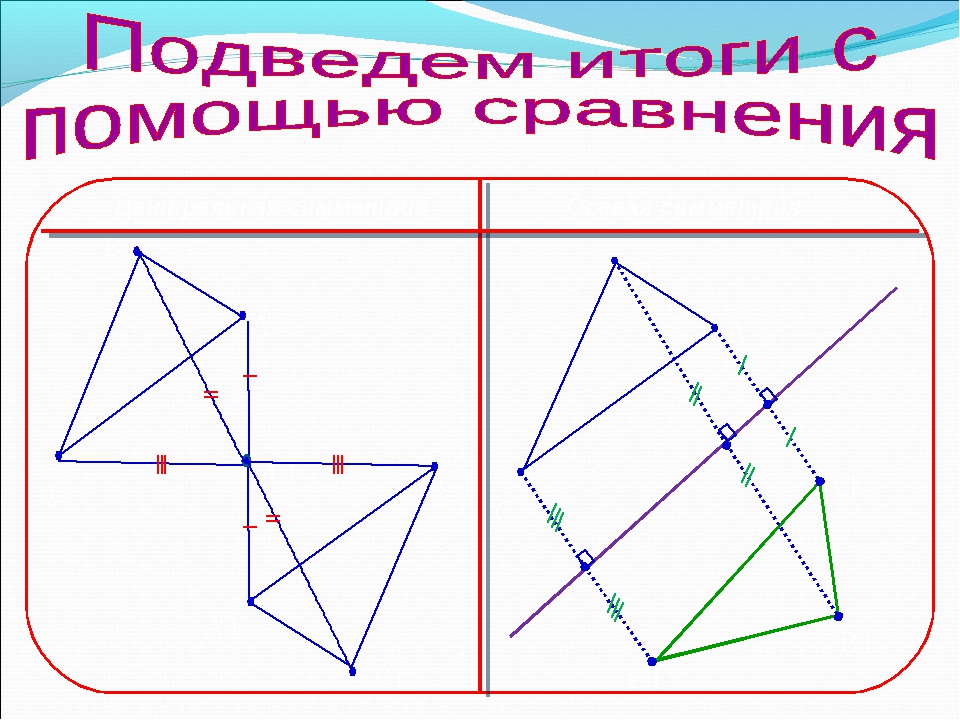 . AA1l.. AA1
. AA1l.. AA1
Номер слайду 12
Свойства симметрия 3. Если отрезки M1 N1 и MN симметричны относительно прямой l, то их длины равны 4. Если А1 симметрична точке А относительно прямой l, то для любой точки В на этой прямойотрезки А1 В и АВ равныl. M1 MN1 Nl. А1 АВ
Номер слайду 13
Построим отображение ломаной АВС относительно прямой l (оси симметрии):1.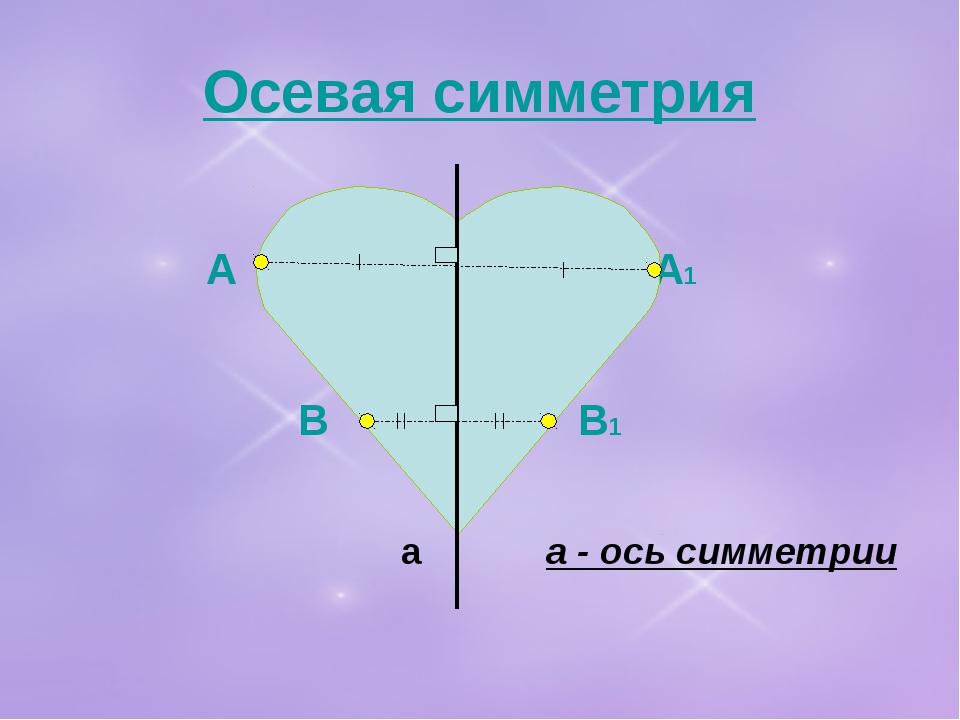 Из вершин А и В опускаем перпендикуляры на прямую l.2. Продолжаем их за прямую l на такое же расстояние (равное длине соответствующего отрезка).3. Соединим полученные точки. Ломаная А1 В1 С1 – отражение АВС. (Точка С осталась на месте. Она лежит на оси симметрии)
Из вершин А и В опускаем перпендикуляры на прямую l.2. Продолжаем их за прямую l на такое же расстояние (равное длине соответствующего отрезка).3. Соединим полученные точки. Ломаная А1 В1 С1 – отражение АВС. (Точка С осталась на месте. Она лежит на оси симметрии)
Номер слайду 14
УСТНО:№ 316, 317 Графическая работа:№ 322, 325 ПИСЬМЕННО:№ 333, 341
Номер слайду 15
Симметрия помогает решать задачи.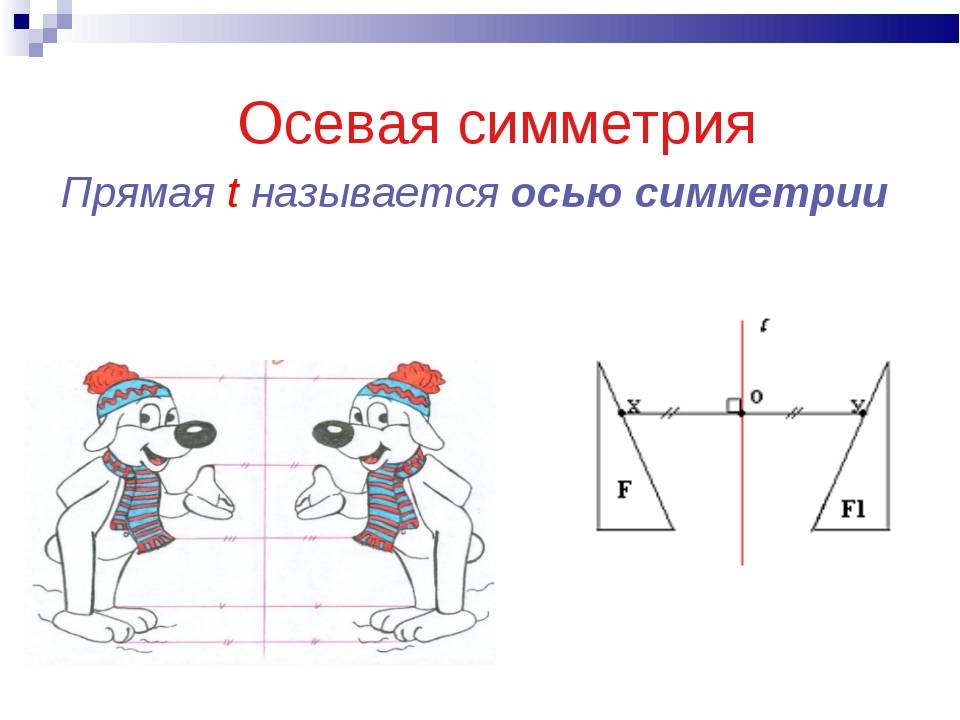 ЗАДАЧА 1 (расстояние от точки до прямой)Если А – некоторая точка плоскости, а В – точка на прямой l, то длина отрезка АВ будет наименьшей, если отрезок АВ перпендикулярен ll. АВЗАДАЧА 2 (касательная к окружности)Прямая перпендикулярная радиусу окружности и проходящая через конец этого радиуса , касается окружности
ЗАДАЧА 1 (расстояние от точки до прямой)Если А – некоторая точка плоскости, а В – точка на прямой l, то длина отрезка АВ будет наименьшей, если отрезок АВ перпендикулярен ll. АВЗАДАЧА 2 (касательная к окружности)Прямая перпендикулярная радиусу окружности и проходящая через конец этого радиуса , касается окружности
Номер слайду 16
Симметрия относительно точки – центральная симметрия
Номер слайду 17
Точка О является центром симметрии, если при повороте вокруг точки О на 1800 фигура переходит сама в себя.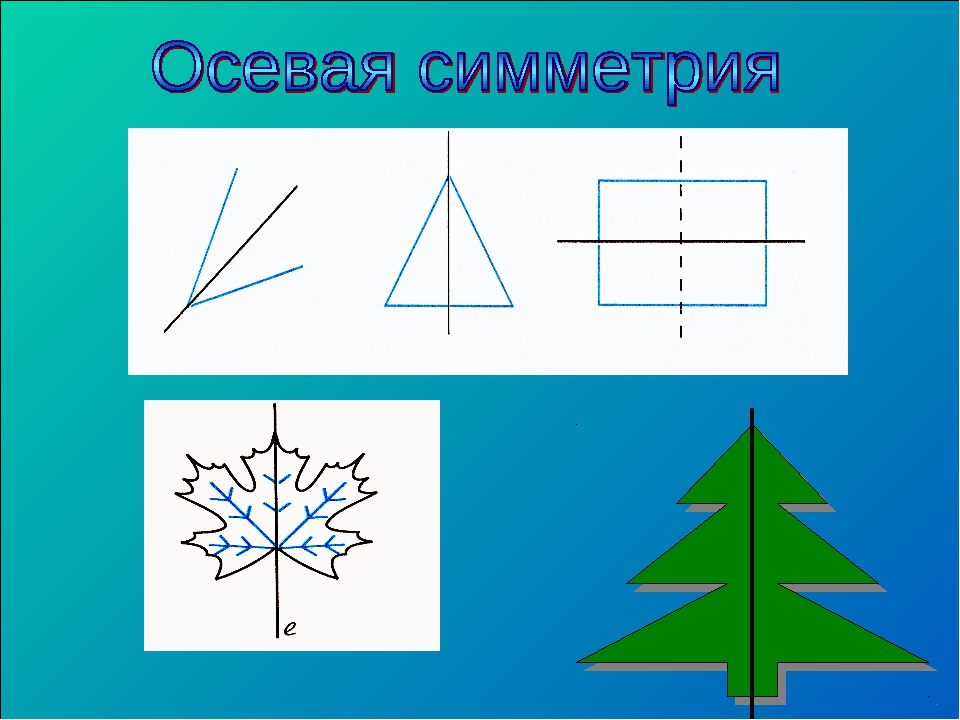 О
О
Номер слайду 18
УСТНО:№ 312, 315 Графическая работа:№ 321, 323 ПИСЬМЕННО:№ 333, 341
Номер слайду 19
№ 323
Номер слайду 20
В биологии винтовая симметрия присуща некоторым вирусам, например капсид вируса табачной мозаики представляет собой 130 витков с шагом спирали 23 Å. Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии. Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.
Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии. Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.
Номер слайду 21
В теоретической физике поведение физической системы описывается некоторыми уравнениями. Инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
Номер слайду 22
Симметрия в религиозных символах:ряд 1. христианском, иудейском, даосийском; ряд 2. исламском, буддийском, синтоистском; ряд 3. сикхском, в вере Бахаи, индуистском.
Номер слайду 23
Домашнее задание: § 10 № 330, 333, 338 Я исследователь: практическая работа. Пусть два зеркала поставлены параллельно друг другу отражающимися поверхностями внутрь. Между ними на бумаге нарисована некоторая линия. Нарисуйте отражениеэтой линии в каждом из зеркал. 2) Два зеркала стоят перпендикулярно друг другу. Между ними нарисована кривая, идущая от зеркала кзеркалу. Сколько раз отразится кривая в зеркалах? Сколько осей симметрии имеет полученная фигура?
Пусть два зеркала поставлены параллельно друг другу отражающимися поверхностями внутрь. Между ними на бумаге нарисована некоторая линия. Нарисуйте отражениеэтой линии в каждом из зеркал. 2) Два зеркала стоят перпендикулярно друг другу. Между ними нарисована кривая, идущая от зеркала кзеркалу. Сколько раз отразится кривая в зеркалах? Сколько осей симметрии имеет полученная фигура?
Номер слайду 24
Учитель математики Богдановской ООШ І – ІІІ ступеней. ШАДЬКО Е. А. Литература: Геометрия 9 класс А. П. Ершова., В. В. Голобородько. Математика. Наглядная геометрия И. Ф. Шарыгин. Материалы из Википедии. Интернет ресурсы
Математика. Наглядная геометрия И. Ф. Шарыгин. Материалы из Википедии. Интернет ресурсы
Какие геометрические фигуры имеют ось симметрии. Как нарисовать симметричный предмет
Фридрих В.А. 1
Дементьева В.В. 1
1 Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 6», г. Александровск, Пермский край
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
«Стоя перед черной доской и рисуя на ней
мелом разные фигуры,
я вдруг был поражен мыслью:
почему симметрия приятна глазу?
Что такое симметрия?
Это врожденное чувство, отвечал я сам себе»
Л.Н. Толстой
В учебнике математика 6 класс, автор Никольский С. М., на страницах 132 — 133 раздел Дополнительные задачи к главе № 3, имеются задания для исследования фигур на плоскости, симметричных относительно прямой. Меня заинтересовала данная тема, я решила выполнить задания и более подробно изучить данную тему.
М., на страницах 132 — 133 раздел Дополнительные задачи к главе № 3, имеются задания для исследования фигур на плоскости, симметричных относительно прямой. Меня заинтересовала данная тема, я решила выполнить задания и более подробно изучить данную тему.
Объект исследования — симметрия.
Предмет исследования — симметрия как основополагающий закон вселенной.
Какую гипотезу я буду проверять:
Я считаю, что осевая симметрия является не только математическим и геометрическим понятием, и применяется только для решения соответствующих задач, но и является основой гармонии, красоты, равновесия и устойчивости. Принцип симметрии используется практически во всех науках, в нашей повседневной жизни и является одним из «краеугольных» законов, на котором базируется мироздание в целом.
Актуальность темы
Понятие симметрия проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков его развития. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живём, наполнен симметрией домов, улиц, творениями природы и человека. С симметрией мы встречаемся буквально на каждом шагу: в технике, искусстве, науке.
Мир, в котором мы живём, наполнен симметрией домов, улиц, творениями природы и человека. С симметрией мы встречаемся буквально на каждом шагу: в технике, искусстве, науке.
Поэтому, знание и понимание о симметрии в окружающем нас мире, является обязательным и необходимым, которое пригодится в дальнейшем для изучения других научных дисциплин. В этом и заключается актуальность избранной мной темы.
Цель и задачи
Цель работы: выяснить, какую роль играет симметрия в повседневной жизни человека, в природе, архитектуре, в быту, музыке и других науках.
Для достижения поставленной цели, мне необходимо выполнить следующие задачи:
1. Найти необходимую информацию, литературу и фотографии. Установить наибольшее количество данных, необходимых для моей работы, с помощью доступных для меня источников: учебники, энциклопедии или другие носители информации, соответствующих заданной теме.
2. Дать общие понятие о симметрии, видах симметрии и истории происхождения термина.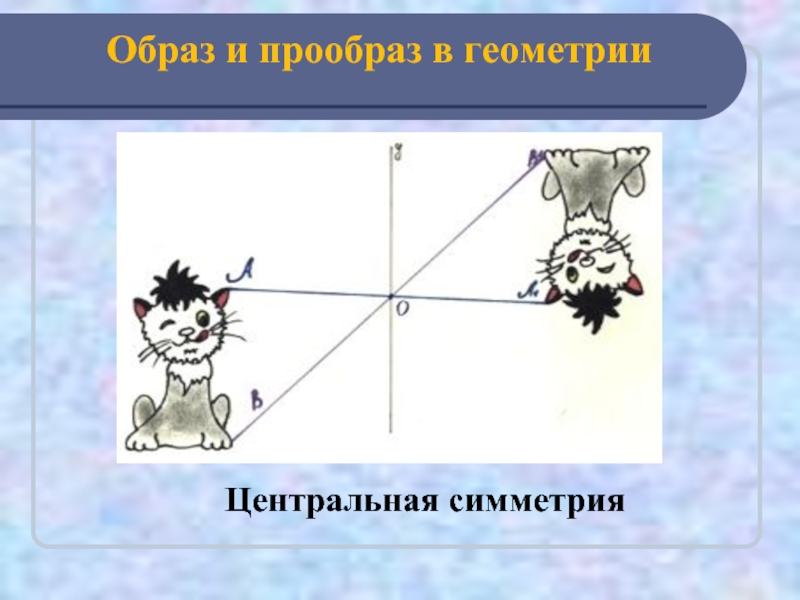
3. Для подтверждения своей гипотезы, создать поделки и провести эксперимент с данными фигурами, имеющими симметрию и не несимметричными.
4. Продемонстрировать и представить результаты наблюдений в своём исследовании.
Для практической части исследовательской работы мне необходимо сделать следующее, для чего я составила план работы:
1. Создать своими руками поделки с заданными свойствами — симметричные и не симметричные модели, композицию, используя цветную бумагу, картон, ножницы, фломастеры, клей и т.д.;
2. Провести эксперимент с моими поделками, с двумя вариантами симметрии.
3. Исследовать, проанализировать и систематизировать полученные результаты, составив таблицу.
4. Для наглядного и интересного закрепления полученных знаний, с помощью приложения «Paint 3 D» создать рисунки для наглядности, а так же нарисовать картинки, с заданиями — дорисовать симметричную половинку (начиная с простых рисунков и заканчивая сложными) и объединить их, создав электронную книгу.
Методы исследования:
1. Анализ статей и всей информации о симметрии.
2. Компьютерное моделирование (обработка фотографий средствами графического редактора).
3. Обобщение и систематизация полученных данных.
Основная часть.
Осевая симметрия и понятие совершенства
С древних времен человек выработал представления о красоте и пытался постигнуть смысл совершенства. Красивы все творения природы. По-своему прекрасны люди, восхитительны животные и растения. Радует взор зрелище драгоценного камня или кристалла соли, сложно не любоваться снежинкой или бабочкой. Но почему так происходит? Нам кажется правильным и завершенным вид объектов, правая и левая половина которых выглядит одинаково.
Видимо, первыми о сути красоты задумывались люди искусства.
Впервые обосновали это понятие художники, философы и математики Древней Греции. Древние скульпторы, изучавшие строение человеческого тела, еще в V веке до н.э. стали применять понятие «симметрия». Это слово имеет греческое происхождение и означает гармоничность, пропорциональность и похожесть расположения составляющих частей. Древнегреческий мыслитель и философ Платон утверждал, что прекрасным может быть лишь то, что симметрично и соразмерно.
Это слово имеет греческое происхождение и означает гармоничность, пропорциональность и похожесть расположения составляющих частей. Древнегреческий мыслитель и философ Платон утверждал, что прекрасным может быть лишь то, что симметрично и соразмерно.
И действительно, «радуют глаз» те явления и формы, которые имеют пропорциональность и завершенность. Их мы называем правильными.
Виды симметрии
В геометрии и математике рассматриваются три вида симметрии: осевая симметрия (относительно прямой), центральная (относительно точки) и зеркальная (относительно плоскости).
Осевая симметрия как математическое понятие
Точки симметричны относительно некой прямой (оси симметрии), если они лежат на прямой, перпендикулярной данной прямой, и на одинаковом расстоянии от оси симметрии.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры, симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Прямая является в этом случае осью симметрии фигуры.
Фигуры, симметричные относительно прямой равны. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.
Примеры оси симметрии: биссектриса неразвернутого угла равнобедренного треугольника, любая прямая, проведенная через центр окружности, и т.д. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.
Фигуры могут иметь несколько осей симметрии:
· осью симметрии угла является прямая, на которой лежит его биссектриса;
· осью симметрии окружности и круга является любая прямая, проходящая через их диаметр;
· равнобедренный треугольник имеет одну ось симметрии, равносторонний треугольник — три оси симметрии;
· прямоугольник имеет 2 оси симметрии, квадрат — 4, ромб — 2 оси симметрии.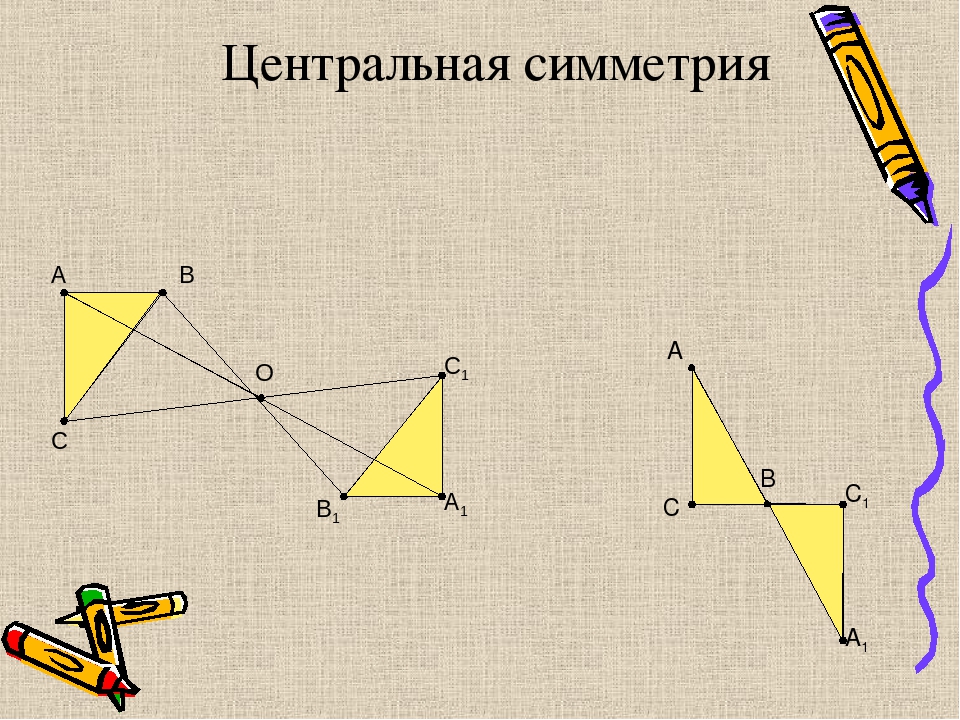
Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На моём рисунке она изображена для наглядности.
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относится параллелограмм, отличный от прямоугольника и ромба, разносторонний треугольник.
Осевая симметрия в природе
Природа мудра и рациональна, поэтому почти все ее творения имеют гармоничное строение. Это относится и к живым существам, и к неодушевленным объектам.
Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия. Ярко выраженной симметрией обладают листья, цветы, плоды. Их зеркальная, радиальная, центральная, осевая симметрия — очевидны. В значительной степени она обусловлена явлением гравитации.
Геометрические формы кристаллов с их плоскими поверхностями представляют собой удивительное явление природы. Однако подлинная физическая симметрия кристалла проявляется не столько в его внешнем виде, сколько во внутреннем строении кристаллического вещества.
Осевая симметрия в животном мире
Симметрия в мире живых существ, проявляется в закономерном расположении одинаковых частей тела относительно центра или оси. Чаще в природе встречается осевая симметрия. Она обуславливает не только общее строение организма, но и возможности его последующего развития. Каждому виду животных присущ характерный окрас. Если в расцветке фигурирует рисунок, то, как правило, он дублируется с обеих сторон.
Осевая симметрия и человек
Если взглянуть на любое живое существо, сразу бросается в глаза симметричность устройства организма. Человек: две руки, две ноги, два глаза, два уха и так далее.
Это означает, что существует некая линия, по которой животные и люди могут быть визуально «поделены» на две идентичные половинки, то есть в основе их геометрического устройства лежит осевая симметрия.
Как видно из приведённых примеров, любой живой организм природа создает не хаотично и бессмысленно, а согласно общим законам мироустройства, ведь во Вселенной ничто не имеет чисто эстетического, декоративного назначения. Это обусловлено закономерной необходимостью.
Это обусловлено закономерной необходимостью.
Конечно, природе редко присуща математическая точность, но похожесть элементов организма все равно поразительна.
Симметрия в архитектуре
С древнейших времен архитекторы хорошо знали математическую пропорцию и симметрию, и использовали их при строительстве архитектурных сооружений. Например, архитектура русских православных храмов и соборов Руси: Кремль, собор Христа Спасителя г. Москва, Казанский и Исаакиевский соборы г. Санкт-Петербург и др.
А также другие всемирно известные достопримечательности, многие из которых во всех странах мира, мы можем видеть и сейчас: Египетские пирамиды, Лувр, Тадж-Махал, Кёльнский собор и т.д. Все они, как мы видим, имеют симметрию.
Симметрия в музыке
Я учусь в музыкальной школе, для меня было интересно найти примеры симметрии в данной области. Не только музыкальные инструменты обладают явной симметрией, но и части музыкальных произведений звучат в определённом порядке, в соответствии с партитурой и замыслом композитора.
Например, реприза — (франц. reprise, от reprendre -возобновлять). Повторение темы или группы тем после этапа её (их) развития или изложения нового тематического материала.
Также в одномерном повторении во времени через равные интервалы состоит музыкальный принцип ритма.
Симметрия в технике
Мы живем в стремительно — меняющемся высокотехнологическом, информационном обществе, и не задумываемся, почему некоторые окружающие нас предметы и явления пробуждают чувство прекрасного, а другие нет. Мы их не замечаем, даже не задумываемся, об их свойствах.
Но кроме этого, данные технические и механические устройства, детали, механизмы, агрегаты не смогут правильно работать и вообще функционировать, если при этом не будет соблюдена симметрия, а вернее, некая ось, в механике это — центр тяжести.
Сбалансированность по центру, в данном случае, является обязательным техническим требованием, соблюдение которого строго регламентируется ГОСТ или ТУ и должно соблюдаться.
Симметрия и космические объекты
Но, пожалуй, самыми загадочными, волновавшими умы многих, ещё с древнейших времён, являются космические объекты. Которые также имеют симметрию — солнце, луна, планеты.
Эту цепочку можно продолжать, но мы сейчас говорим о чем-то едином: о том, что осевая симметрия является основополагающим законом вселенной, является основой красоты, гармонии и пропорциональности, и во взаимосвязи этого с математикой.
Практическая часть
Найдя необходимую информацию, изучив литературу, я убедилась в правоте своей гипотезы и сделала вывод о том, что в глазах человека несимметричность чаще всего ассоциируется с неправильностью или ущербностью. Поэтому в большинстве творений людских рук прослеживается симметричность и гармония, как необходимое и обязательное требование.
Это хорошо видно на моём рисунке, где изображён поросёнок, с непропорциональными частями тела, что сразу бросается в глаза!
И только после того, как подольше приглядишься к нему, посчитаешь его милым?
Несмотря на то, что данная тема известна, хорошо изучена, но все эти данные рассмотрены отдельно в каждой дисциплине. Обобщённых данных о том, что принцип симметрии используется, и именно на нём базируются многие другие науки, и их взаимосвязи с математикой я не встретила.
Обобщённых данных о том, что принцип симметрии используется, и именно на нём базируются многие другие науки, и их взаимосвязи с математикой я не встретила.
Поэтому я решила доказать своё утверждение с помощью самого простого и доступного для меня способа. Таким решением, я считаю, будет проведение эксперимента с испытаниями.
Для наглядного доказательства того, что асимметричные модели не устойчивы, не обладают необходимыми требованиями и жизненно необходимыми навыками, и подтверждения своей гипотезы мне необходимо создать поделки, рисунки и композицию:
1 вариант — симметричны относительно оси;
2 вариант — с явным нарушением симметрии.
Поскольку я считаю, что такой дисбаланс будет хорошо виден на следующих примерах, для чего я создала поделки-оригами (самолёт и лягушонок) из цветной бумаги. Для чистоты эксперимента они сделаны из одинаковой цветной бумаги и тестировались в одинаковых условиях. И композицию «Маяк», где маяк сделан из пустой пластиковой бутылки, обклеен цветной бумагой. Для украшения композиции использованы игрушечные фигуры человека, модели парусника и лодки, декоративные камни, а для имитации света я использовала светящийся от батарейки элемент.
Для украшения композиции использованы игрушечные фигуры человека, модели парусника и лодки, декоративные камни, а для имитации света я использовала светящийся от батарейки элемент.
Я провела испытания с данными поделками, все показатели зафиксировала и занесла в таблицу (все показатели можно посмотреть в приложении № 1 стр. 18 — 21).
Все поделки делались с соблюдением техники безопасности (приложение № 2 стр. 21)
Все полученные данные я проанализировала, вот что у меня получилось.
Анализ полученных данных
Эксперимент № 1
Испытание — прыжок лягушек в длину, замер этого расстояния.
Лягушонок Зелёный (симметричный) прыгает ровно, на большее расстояние, а Красный (не симметричный) ни разу не прыгнул ровно, всегда с поворотом или переворотом в сторону, на расстояние в 2 — 3 раза меньше.
Таким образом, можно сделать вывод, что такое животное не сможет быстро охотиться или наоборот убегать, эффективно добывать пищу, что уменьшает шансы на выживание, это доказывает, что в природе всё сбалансировано, пропорционально, правильно — симметрично.
Эксперимент № 2
Вид испытания — запуск самолётов в полёт и измерение расстояния длины полёта.
Самолётик № 1 «Розовый» (симметричный) летит из 10 раз, 8 раз ровно и прямо, на максимальную длину, (т.е. на всю длину моей комнаты), а траектория полёта самолётика № 2 «Оранжевый» (не симметричный) из 10 раз — ни разу не летел ровно, всегда с поворотом или переворотом, на меньшее расстояние. То есть, если бы это был настоящий самолёт, то он не смог бы лететь ровно, в правильном направлении. Такой полёт был бы очень неудобен или даже опасен для человека (также как и для птиц), а машины и другие транспортные средства передвижения, не смогли бы ехать, плыть и т.д. в необходимую сторону.
Эксперимент № 3
Вид испытания — проверка устойчивости здания «Маяка», при уменьшении угла наклона сооружения, относительно поверхности.
1. Создав композицию «Маяка», я установила его прямо, т.е. перпендикулярно (под углом 90 0) относительно стен сооружения к поверхности.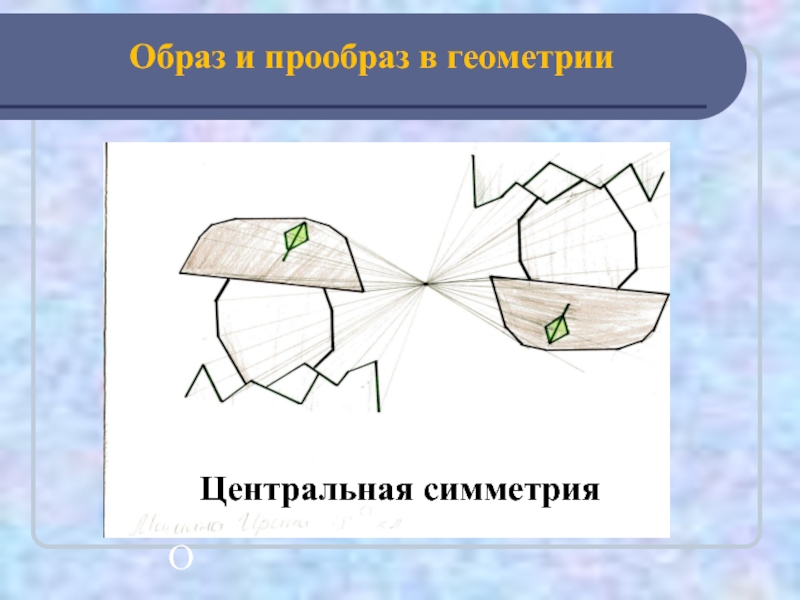 Данная конструкция стоит ровно, выдерживает установленный световой элемент и фигурку человека.
Данная конструкция стоит ровно, выдерживает установленный световой элемент и фигурку человека.
2. Для дальнейшего проведения эксперимента мне было необходимо расчертить основание башни на углы, равные 10 0 .
После чего я отрезала от основания угол равный 10 0 .
Под углом в 80 0 здание стоит криво, шатается, но дополнительную нагрузку выдерживает.
3. Отрезав ещё 10 0 , получился угол наклона в 70 0 , при котором вся моя конструкция рушится.
Данный опыт доказывает, что исторически сложившиеся традиция строительства под прямым углом и соблюдение при этом симметрии самого здания, является необходимым условием для устойчивого, надёжного возведения и эксплуатации архитектурных зданий и сооружений.
Для наглядного примера осевой симметрии и доказательства утверждения о том, что человек воспринимает любые окружающие его предметы, образы животных и т.д. только симметрично, то есть, когда обе стороны, «половинки» одинаковы, равны, я создала электронную раскраску, которую можно распечатать, составив детскую книжку-раскраску.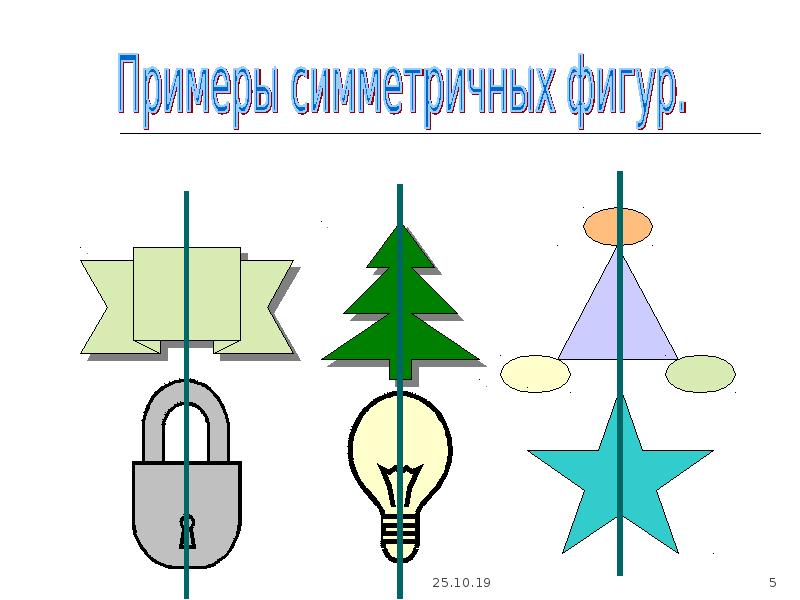 Данное пособие поможет всем желающим лучше усвоить тему, интересно и с удовольствием провести свободное время (Титульный лист изображён на этом рисунке, остальные рисунки расположены в приложении № 3 стр. 21 -24).
Данное пособие поможет всем желающим лучше усвоить тему, интересно и с удовольствием провести свободное время (Титульный лист изображён на этом рисунке, остальные рисунки расположены в приложении № 3 стр. 21 -24).
Проведённые мною эксперименты доказывают, что симметрия является не только математическим и геометрическим понятием, а является сферой, средой нашего проживания, неким техническим требованием, так же необходимым условием для выживания в целом, как для людей, так и для животных. Симметрия объединяет всё это воедино, и уходит далеко за пределы обычной науки!
Заключение
Выводы:
Я выяснила, что симметрия является одной из главных составляющих в повседневной жизни человека, в предметах быта, в архитектуре, технике, в природе, музыке, науке и т. д.
Результат:
Я нашла необходимую информацию, доказала свою гипотезу, проверила и подтвердила её опытным путём. Я создала поделки, композицию, рисунки и электронную раскраску для наглядного проведения эксперимента.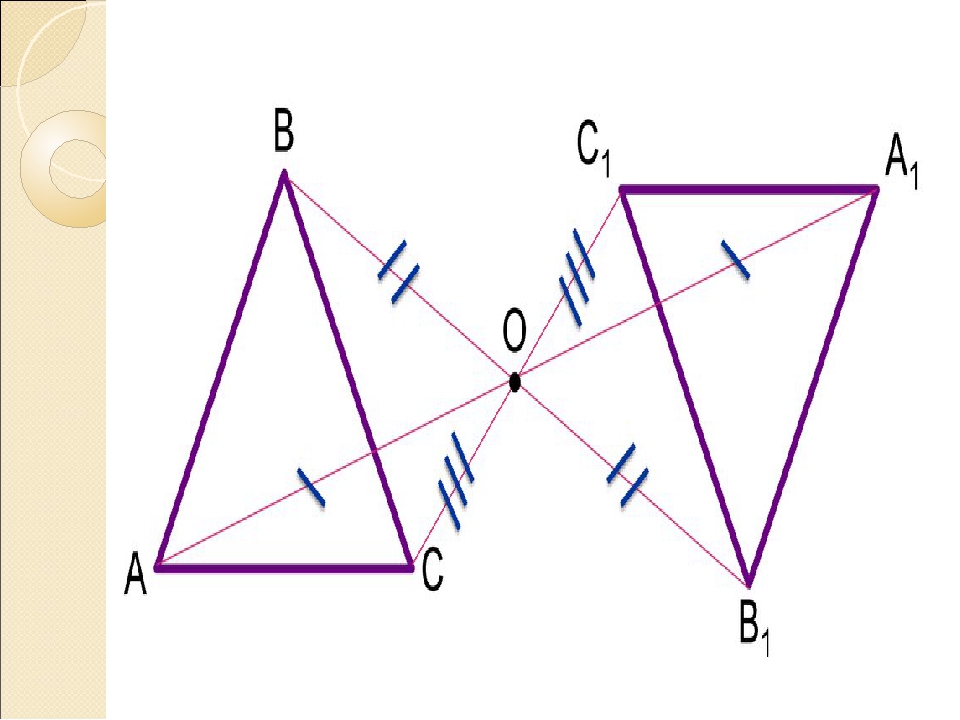
Я выяснила, что все законы природы — биологические, химические, генетические, астрономические связаны с симметрией. Практически, всё то, что нас окружает, что создано человеком — подчинено общим для нас всех принципам симметрии, поскольку имеют завидную системность. Таким образом, сбалансированность, тождественность как принцип имеет всеобщий масштаб.
Можно сказать, что симметрия является основополагающим законом, на котором базируются основные законы науки? Наверное, да.
Эту тайну пытались осмыслить великие мыслители человечества. Сегодня в разгадку этой тайны погрузились и мы.
Один из известных математиков Герман Вейль писал, что «симметрия — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».
Может мы нашли секрет создания красоты, совершенства или даже создания основных законов вселенной? Может это симметрия?
Приложения
Приложение № 1 Таблица испытаний:
Эксперимент № 1 | |||
Попытка № | Вид испытания | «Зелёная лягушка» (симметричная) | Результат и характеристика испытания «Красная лягушка» (не симметричная) |
Прыжок лягушки в длину (измерение в см. | 6,0 в левую сторону | ||
14,4 с небольшим поворотом вправо | 9,0 переворот назад | ||
10,5 почти ровно | 2,0 переворот | ||
9,5 с небольшим поворотом вправо | 5,0 переворот в левую сторону | ||
10,6 с небольшим поворотом вправо | 3,0 в левую сторону | ||
9,0 переворот | 9,0 поворот влево | ||
13,5 почти ровно | 1,5 назад, с поворотом влево | ||
9,5 влево с переворотом | |||
21,2 почти ровно | 4,5 влево с переворотом | ||
Эксперимент № 2 | |||
Самолёт «Розовый» (Симметричный) | Самолёт «Оранжевый» (Не симметричный) | ||
Запуск самолётика в длину Максимальная (5,1 метра) | 5,1 с 2 переворотами | 3,04 с переворотами вправо | |
2,78 с переворотами вправо | |||
5,1 с наклоном вправо | 3, 65 с переворотами вправо | ||
5,1 с наклоном вправо | 1,51 почти ровно | ||
5,1 почти ровно | 4,73 с переворотами вправо | ||
5,1 с наклоном в левую сторону | 3,82 поворот вправо | ||
5,1 почти ровно | 3,41 с переворотами | ||
5,1 почти ровно | 3,37 поворот влево | ||
5,1 с переворотом | 3,51 с переворотами влево | ||
5,1 почти ровно | 3,19 с переворотами вправо | ||
Эксперимент № 3 | |||
Попытка № | Характеристика свойств объекта | Вид и характеристика испытания | Результат |
Сооружение стоит перпендикулярно поверхности (т. | Установка дополнительной нагрузки: светящийся элемент и игрушечная фигура человека | Маяк стоит ровно, надёжно | |
Под углом 80 0 | От основания маяка я наметала и отрезала угол в 10 0 | Маяк выдерживает нагрузку, но стоит ненадёжно, шатается | |
Под углом 70 0 | От основания маяка я ещё раз отрезала 10 0 | Сооружение падает и рушится | |
Приложение № 2
При изготовлении моих поделок соблюдалась техника безопасности, а именно:
Ножницы или нож должны быть хорошо заточены и отрегулированы.
Хранить необходимо в определенном и безопасном месте или коробке.
При пользовании ножниц (ножа), нельзя отвлекаться, нужно быть максимально внимательными, дисциплинированными.
Передавая ножницы (нож), держать их за сомкнутые лезвия (остриё).
Ножницы (нож) класть справа сомкнутыми лезвиями (остриём) направленными от себя.
При резании узкое лезвие ножниц (остриё ножа) должно быть внизу.
После использования клея вымыть руки.
Приложение № 3
Электронная книга-раскраска
Симметрия-
Это означает то, что одна часть предмета похожа на другую.
Осевая симметрия- это симметрия относительно прямой (линии).
Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На рисунках она изображена для наглядности.
В этой книге нужно закончить рисунки, соединяя точки.
Затемможнораскрашиватьто, чтополучилось.
Попробуй закончить эти рисунки:
Сердечко
Треугольник Домик
Звёздочка Листочек
Мышка Ёлочка
Собачка Замок
К роме осевой симметрии есть и симметрия относительно точки.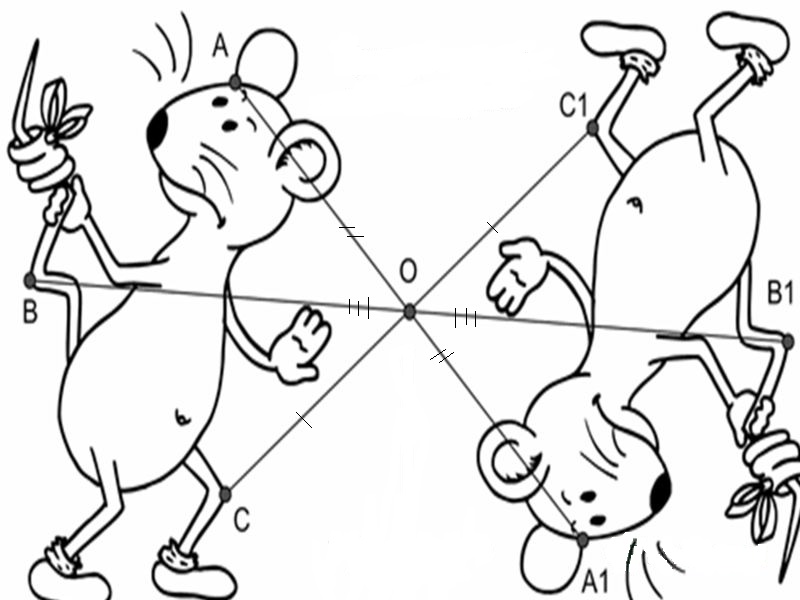
Этот шар симметричен
И ёщё один вид симметрии — зеркальная симметрия.
Зеркальная симметрия-
это симметрия относительно плоскости. Например, относительно зеркала.
Симметрия это—
Используемая литература
2. Герман Вейль «Симметрия» (Издательство «Наука» главная редакция физико-математической литературы, Москва 1968 г.)
4. Мои рисунки и фотографии.
5. Справочник машиностроителя, том 1, (Государственное научно — техническое издательство машиностроительной литературы, Москвы 1960 г.)
6. Фотографии и рисунки из сети «Интернет».
Цели:
- образовательные:
- дать представление о симметрии;
- познакомить с основными видами симметрии на плоскости и в пространстве;
- выработать прочные навыки построения симметричных фигур;
- расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
- показать возможности использования симметрии при решении различных задач;
- закрепить полученные знания;
- общеучебные:
- научить настраивать себя на работу;
- научить вести контроль за собой и соседом по парте;
- научить оценивать себя и соседа по парте;
- развивающие:
- активизировать самостоятельную деятельность;
- развивать познавательную деятельность;
- учить обобщать и систематизировать полученную информацию;
- воспитательные:
- воспитываать у учащихся “чувство плеча”;
- воспитывать коммуникативность;
- прививать культуру общения.

ХОД УРОКА
Перед каждым лежат ножницы и лист бумаги.
Задание 1 (3 мин).
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).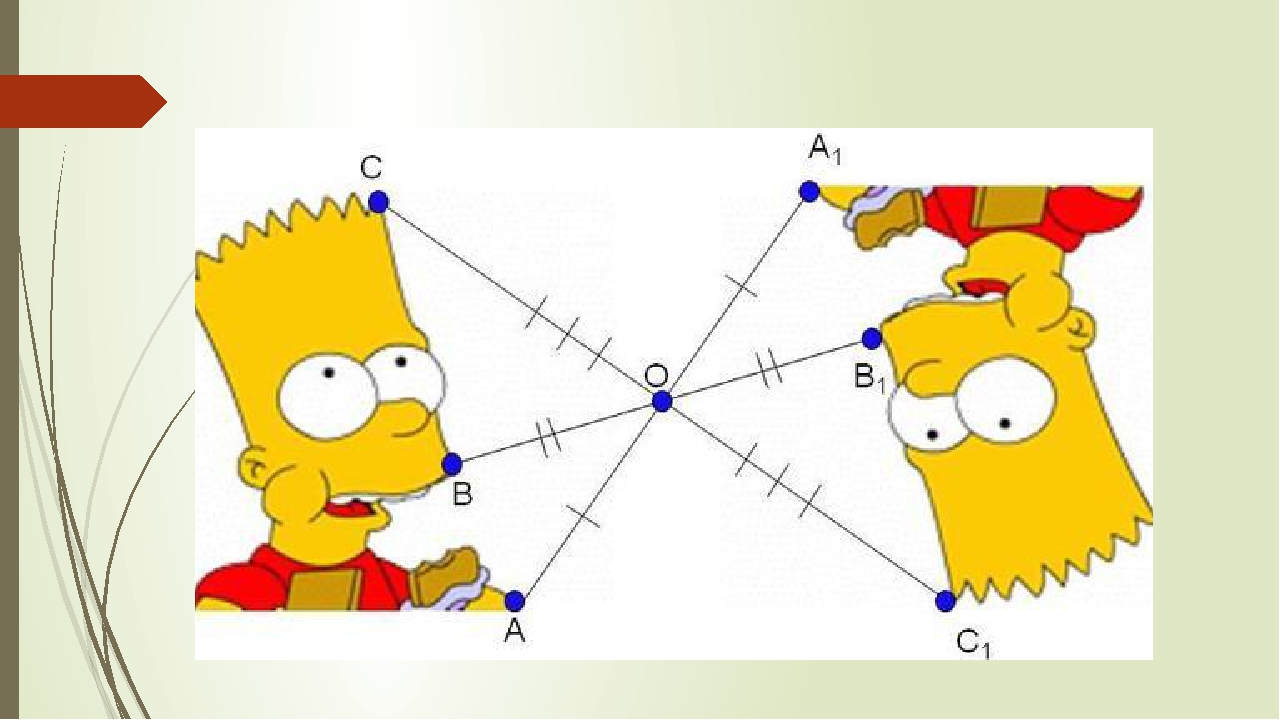
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии.Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
Задание 4 (3 мин).
– Используя полученную информацию, долепить
недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
Задание 6 (2 мин).
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных
треугольников с общим основанием равным 6 см.
Начертите в тетради несколько равнобедренных
треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме
относятся к очень отдаленной эпохе древнего
каменного века – палеолита. В течение сотен
тысячелетий этого периода люди жили в пещерах, в
условиях мало отличавшихся от жизни животных.
Люди изготовляли орудия для охоты и рыболовства,
вырабатывали язык для общения друг с другом, а в
эпоху позднего палеолита украшали свое
существование, создавая произведения искусства,
статуэтки и рисунки, в которых обнаруживается
замечательное чувство формы.
Когда произошел переход от простого собирания
пищи к активному ее производству, от охоты и
рыболовства к земледелию, человечество вступает
в новый каменный век, в неолит.
Человек неолита обладал острым чувством
геометрической формы. Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
Задание на дом:
1. Придумать свой орнамент, изобразить его на
листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют
элементы симметрии.
В широком смысле симметрией именуется сохранение чего-либо неизменным при каких-то преобразованиях. Обладают таким свойством и некоторые геометрические фигуры.
Геометрическая симметрия
Применительно к геометрической фигуре означает, что если данную фигуру преобразовать – например, повернуть – некоторые ее свойства останутся прежними.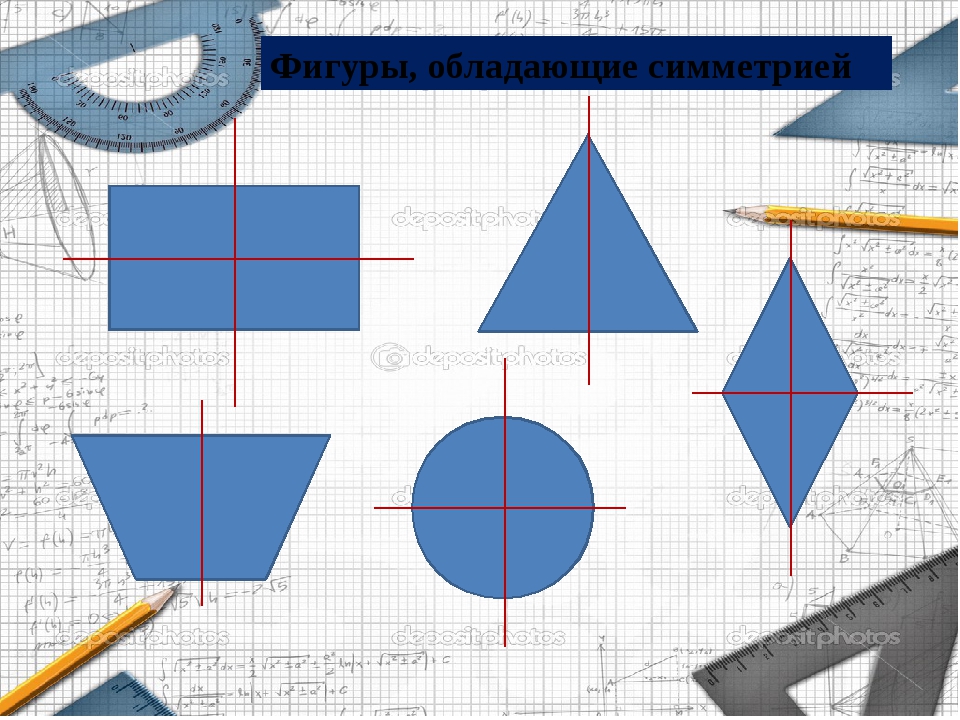
Возможность таких преобразований различается от фигуры к фигуре. Например, круг можно сколько угодно вращать вокруг точки, расположенной в его центре, он так и останется кругом, ничто для него не изменится.
Понятие симметрии можно объяснить, не прибегая к вращению. Достаточно провести через центр круга прямую и построить в любом месте фигуры перпендикулярный ей отрезок, соединяющий две точки на окружности. Точка пересечения с прямой будет делить на две части, которые будут равны друг другу.
Иными словами, прямая разделила фигуру на две равные части. Точки частей фигуры, расположенные на прямых, перпендикулярных данной, находятся на равном расстоянии от нее. Вот эта пряма и будет называться осью симметрии. Симметрия такого рода – – называется осевой симметрией.
Количество осей симметрии
У количество будет различным. Например, у круга и шара таких осей множество. У равностороннего треугольника осью симметрии будет перпендикуляр, опущенный на каждую из сторон, следовательно, у него три оси. У квадрата и прямоугольника можно провести четыре оси симметрии. Две из них перпендикулярны сторонам четырехугольников, а две другие являются диагоналями. А вот у равнобедренного треугольника ось симметрии только одна, располагающаяся меду равными его сторонами.
У квадрата и прямоугольника можно провести четыре оси симметрии. Две из них перпендикулярны сторонам четырехугольников, а две другие являются диагоналями. А вот у равнобедренного треугольника ось симметрии только одна, располагающаяся меду равными его сторонами.
Осевая симметрия встречается и в природе. Ее можно наблюдать в двух вариантах.
Первый вид – радиальная симметрия, предполагающая наличие нескольких осей. Она характерна, например, для морских звезд. Более высокоразвитым организмам присуща билатеральная, или двусторонняя симметрия с единственной осью, делящей тело на две части.
Человеческому телу тоже присуща билатеральная симметрия, но идеальной ее назвать нельзя. Симметрично расположены ноги, руки, глаза, легкие, но не сердце, печень или селезенка. Отклонения от билатеральной симметрии заметны даже внешне. Например, крайне редко бывает так, чтобы у человека на обеих щеках были одинаковые родинки.
Вам понадобится
- — свойства симметричных точек;
- — свойства симметричных фигур;
- — линейка;
- — угольник;
- — циркуль;
- — карандаш;
- — лист бумаги;
- — компьютер с графическим редактором.

Инструкция
Проведите прямую a, которая будет являться осью симметрии. Если ее координаты не заданы, начертите ее произвольно. С одной стороны от этой прямой поставьте произвольную точку A. необходимо найти симметричную точку.
Полезный совет
Свойства симметрии постоянно используются в программе AutoCAD. Для этого используется опция Mirror. Для построения равнобедренного треугольника или равнобедренной трапеции достаточно начертить нижнее основание и угол между ним и боковой стороной. Отразите их с помощью указанной команды и продлите боковые стороны до необходимой величины. В случае с треугольником это будет точка их пересечения, а для трапеции — заданная величина.
С симметрией вы постоянно сталкиваетесь в графических редакторах, когда пользуетесь опцией «отразить по вертикали/горизонтали». В этом случае за ось симметрии берется прямая, соответствующая одной из вертикальных или горизонтальных сторон рамки рисунка.
Источники:
- как начертить центральную симметрию
Построение сечения конуса не такая уж сложная задача.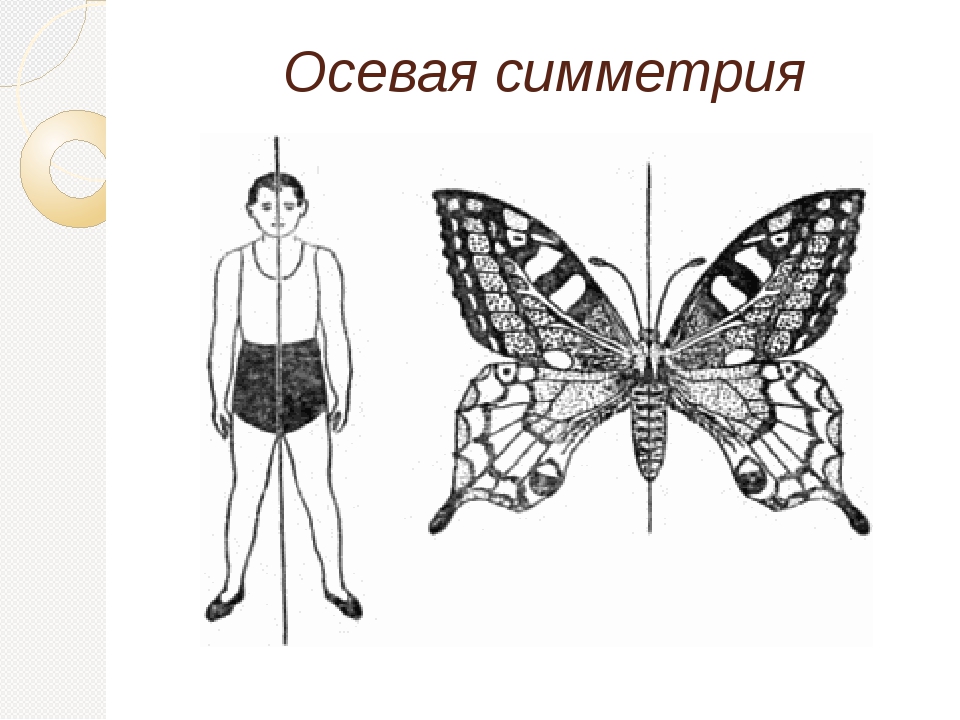 Главное — соблюдать строгую последовательность действий. Тогда данная задача будет легко выполнима и не потребует от Вас больших трудозатрат.
Главное — соблюдать строгую последовательность действий. Тогда данная задача будет легко выполнима и не потребует от Вас больших трудозатрат.
Вам понадобится
- — бумага;
- — ручка;
- — циркль;
- — линейка.
Инструкция
При ответе на этот вопрос, сначала следует определиться – какими параметрами задано сечение.
Пусть это будет прямая пересечения плоскости l с плоскостью и точка О, которая местом пересечения с его сечением.
Построение иллюстрирует рис.1. Первый шаг построения сечения – это через центр сечения его диаметра, продленного до l перпендикулярно этой линии. В итоге получается точка L. Далее через т.О проведите прямую LW, и постройте две направляющие конуса, лежащие в главном сечении О2М и О2С. В пересечении этих направляющих лежат точка Q, а также уже показанная точка W. Это первые две точки искомого сечения.
Теперь проведите в основании конуса ВВ1 перпендикулярный МС и постройте образующие перпендикулярного сечения О2В и О2В1. В этом сечении через т.О проведите прямую RG, параллельную ВВ1. Т.R и т.G — еще две точки искомого сечения. Если бы сечения бал известен, то его можно было бы построить уже на этой стадии. Однако это вовсе не эллипс, а нечто эллипсообразное, имеющее симметрию относительно отрезка QW. Поэтому следует строить как можно больше точек сечения, чтобы соединяя их в дальнейшем плавной кривой получить наиболее достоверный эскиз.
В этом сечении через т.О проведите прямую RG, параллельную ВВ1. Т.R и т.G — еще две точки искомого сечения. Если бы сечения бал известен, то его можно было бы построить уже на этой стадии. Однако это вовсе не эллипс, а нечто эллипсообразное, имеющее симметрию относительно отрезка QW. Поэтому следует строить как можно больше точек сечения, чтобы соединяя их в дальнейшем плавной кривой получить наиболее достоверный эскиз.
Постройте произвольную точку сечения. Для этого проведите в основании конуса произвольный диаметр AN и постройте соответствующие направляющие О2A и O2N. Через т.О проведите прямую, проходящую через PQ и WG, до ее пересечения с только что построенными направляющими в точках P и E. Это еще две точки искомого сечения. Продолжая так же и дальше, можно сколь угодно искомых точек.
Правда, процедуру их получения можно немного упростить пользуясь симметрией относительно QW. Для этого можно в плоскости искомого сечения провести прямые SS’, параллельные RG до пересечения их с поверхность конуса. Построение завершается скруглением построенной ломаной из хорд. Достаточно построить половину искомого сечения в силу уже упомянутой симметрии относительно QW.
Построение завершается скруглением построенной ломаной из хорд. Достаточно построить половину искомого сечения в силу уже упомянутой симметрии относительно QW.
Видео по теме
Вам требуется начертить график тригонометрической функции ? Освойте алгоритм действий на примере построения синусоиды. Для решения поставленной задачи используйте метод исследования.
Вам понадобится
- — линейка;
- — карандаш;
- — знание основ тригонометрии.
Инструкция
Видео по теме
Обратите внимание
Если две полуоси однополосного гиперболоида равны, то фигуру можно получить путем вращения гиперболы с полуосями, одна из которых вышеуказанная, а другая, отличающаяся от двух равных, вокруг мнимой оси.
Полезный совет
При рассмотрении этой фигуры относительно осей Oxz и Oyz видно, что ее главными сечениями являются гиперболы. А при разрезе данной пространственной фигуры вращения плоскостью Oxy ее сечение представляет собой эллипс. Горловой эллипс однополосного гиперболоида проходит через начало координат, ведь z=0.
Горловой эллипс однополосного гиперболоида проходит через начало координат, ведь z=0.
Горловой эллипс описывается уравнением x²/a² +y²/b²=1, а другие эллипсы составляются по уравнению x²/a² +y²/b²=1+h²/c².
Источники:
- Эллипсоиды, параболоиды, гиперболоиды. Прямолинейные образующие
Форма пятиконечной звезды повсеместно используется человеком с древних времен. Мы считаем ее форму прекрасной, так как бессознательно различаем в ней соотношения золотого сечения, т.е. красота пятиконечной звезды обоснована математически. Первым описал построение пятиконечной звезды Евклид в своих «Началах». Давайте же приобщимся к его опыту.
Вам понадобится
- линейка;
- карандаш;
- циркуль;
- транспортир.
Инструкция
Построение звезды сводится к построению с последующим соединением его вершин друг с другом последовательно через одну. Для того чтобы построить правильный необходимо разбить окружность на пять .
Постройте произвольную окружность при помощи циркуля. Обозначьте ее центр точкой O.
Отметьте точку A и при помощи линейки начертите отрезок ОА. Теперь необходимо разделить отрезок OA пополам, для этого из точки А проведите дугу радиусом ОА до пересечения ее с окружностью в двух точках M и N. Постройте отрезок MN. Точка Е, в которой MN пересекает OA, будет делить отрезок OA пополам.
Восстановите перпендикуляр OD к радиусу ОА и соедините точку D и E. Сделайте засечку B на OA из точки E радиусом ED.
Теперь при помощи отрезка DB разметьте окружность на пять равных частей. Обозначьте вершины правильного пятиугольника последовательно цифрами от 1 до 5. Соедините точки в следующей последовательности: 1 с 3, 2 с 4, 3 с 5, 4 с 1, 5 с 2. Вот и правильная пятиконечная звезда, в правильный пятиугольник. Именно таким способом строил
20 мая 2014Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах.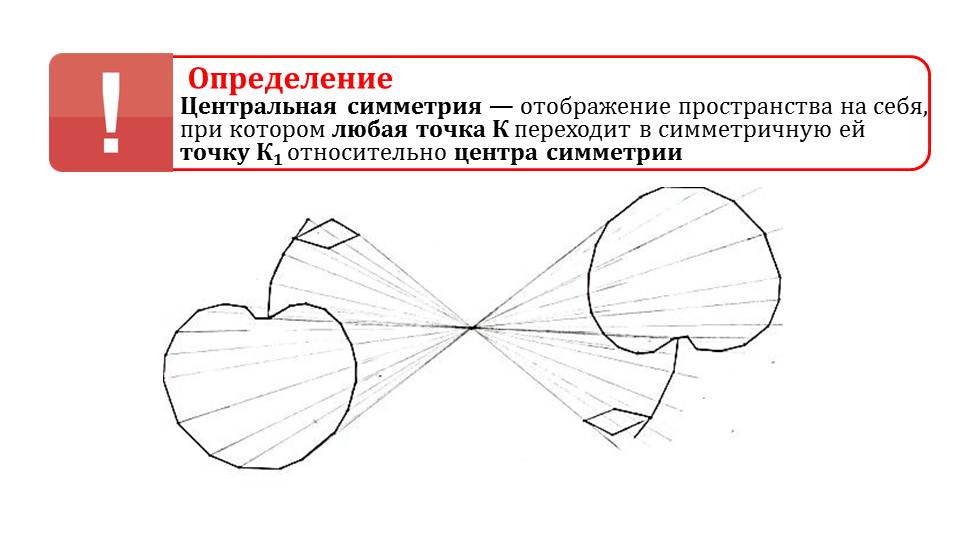 Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Употребление термина в других научных областях
В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Видео по теме
Классификация
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:
Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:
- скользящая;
- вращательная;
- точечная;
- поступательная;
- винтовая;
- фрактальная;
- и т.
 д.
д.
В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.
Базовые элементы
В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.
Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.
Оси
Часто элементом, относительно которого фигуру можно назвать симметричной,
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются оси симметрии фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.
Примерами могут служить равнобедренные и равносторонние треугольники. В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.
Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.
Примеры в геометрии
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все правильные многоугольники, окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.
Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда. Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет.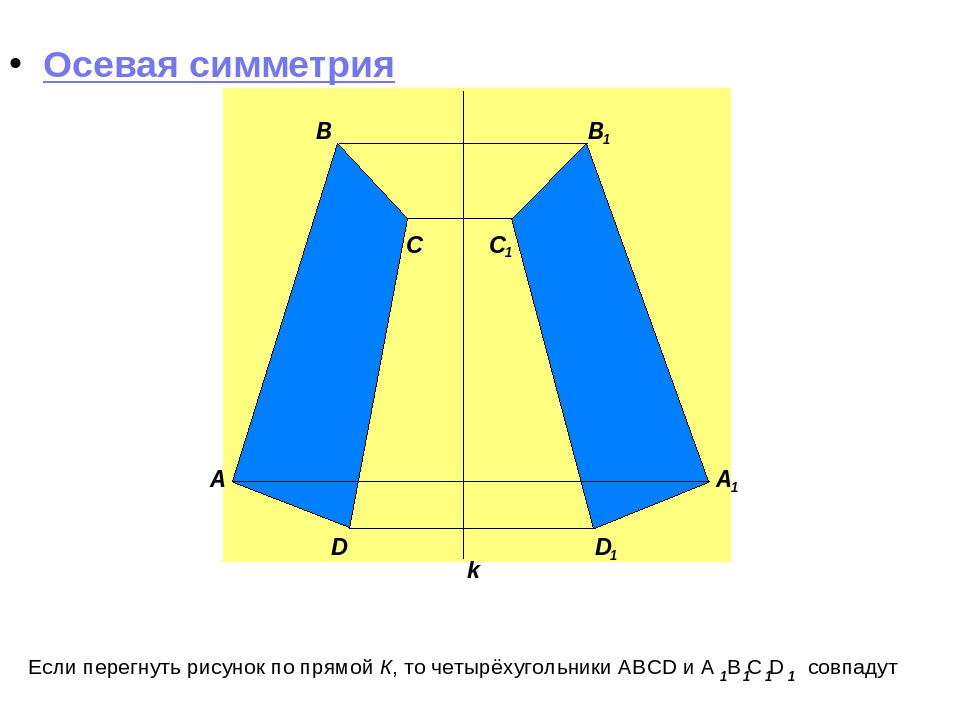 Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие. Каждый случай необходимо рассматривать отдельно.
Примеры в природе
Зеркальная симметрия в жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.
Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.
д. Примеров огромное количество, они буквально везде вокруг.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая Пизанская башня чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Творческая геометрия: как нарисовать симметричную мандалу » 1Gai.Ru
Лайфхак: простой способ рисовать мандалы
В этом видео вы узнаете, как при помощи простого и пары цветных карандашей, нескольких разноцветных фломастеров, транспортира, линейки и циркуля увлечь себя на ближайшие 15-20 минут релаксирующим занятием – рисованием геометрической мандалы.
Хотя, если быть точным, это не совсем мандала, а скорее просто красивая геометрическая фигура, похожая по принципу начертания на мандалу. Другим она напоминает цветок, третьи видят 3D-эффект выпуклой линзы. Но как бы то ни было, при должном старании и аккуратности у вас получится ее нарисовать.
Вам даже не придется утруждаться, учиться рисовать, да и вообще этого уметь не нужно – даже ребенок справится! Отбросьте свои сомнения! Просто достаньте из стола требуемые принадлежности для рисования и включайте видео. Посмотрите его и отметьте для себя самые важные этапы. Не волнуйтесь – если не знаете, с чего начать, мы вам поможем, подсказки будут под видео.
Но прежде чем приступить, сделаем небольшую отсылку на тему, что такое мандала.
Манда́ла – замкнутая геометрическая система с равноудаленными от центральной точки элементами. Сакральное схематическое изображение либо конструкция, используемая в буддийских и индуистских религиозных и эзотерических практиках.
Мандала символизирует сферу обитания божеств, чистые земли будд. В принципе, мандала – это геометрический символ сложной структуры, который интерпретируется как модель Вселенной, «карта космоса», поясняет нам Википедия .
Вооружившись знаниями, переходим к начертанию:
Видео взято с YouTube-канала «Art Therapy and Drawings Tricks»
Основные моменты, о которых нужно помнить при работе над изображением
1. Начертите круг диаметром порядка 10 см.
Начертите круг диаметром порядка 10 см.
2. Держите иглу циркуля крепко прижатой к листу бумаги и основанию под ним. Есть риск, что она соскользнет и рисунок будет испорчен.
А поработать циркулем придется немало.
3. «Разделите» круг на четыре части, выставив линейку через его центр (где была игла циркуля). Поставьте отметки по окружности.
4. При помощи транспортира (не обязательно полностью круглого) поставьте точки через каждый сантиметр, ориентируясь по ранее сделанным четырем отметкам.
5. Это точки, на которые вы будете ставить острие циркуля. Шаг инструмента не изменяем. Круги должны быть точно такими же, как первый, и проходить окружностью через центр, вот так:
И далее все просто – делаем, как показано на видеоролике. При этом не забываем пользоваться карандашами соответствующего тона для увеличения насыщенности рисунка. Приятной вам релаксации!
Приятной вам релаксации!
Осевая и центральная симметрии
Наверняка, каждый из вас не раз слышал слово «симметричный». К чему же это интересное слово можно отнести?
Возьмем, к примеру, листок какого-нибудь растения. Если сложить его пополам, то можно заметить, что каждая из получившихся частей (левая и правая) окажутся одинаковыми, т.е. симметричными.
Аналогично можно поступить и с некоторыми цветами.
В животном мире также можно заметить такую особенность. Вот, например, посмотрим на бабочку. Ее крылья симметричны относительно тельца.
А если посмотреть на здания, которые нас окружают? То снова заметим симметричные части. То же самое вы можете обнаружить в искусстве, да и просто в быту.
Теперь поговорим о том, что же в математике понимают под словом «симметричный», или «симметрия».
В переводе с греческого слово «симметрия»
означает соразмерность, то есть схожесть, одинаковость. Это свойство
геометрических объектов сохранять расположение элементов фигуры относительно
оси или центра симметрии в неизменном состоянии при некоторых преобразованиях.
Это свойство
геометрических объектов сохранять расположение элементов фигуры относительно
оси или центра симметрии в неизменном состоянии при некоторых преобразованиях.
На этом уроке мы поговорим об осевой симметрии (симметрии относительно прямой) и о центральной симметрии (симметрии относительно точки).
Начнём с осевой симметрии.
Точки и называются симметричными относительно прямой , если эта прямая проходит через середину отрезка и перпендикулярна отрезку .
Давайте найдём точку симметричную данной относительно прямой.
Возьмём прямую а и точку А. Проведём через точку А прямую АО, перпендикулярную прямой а. Затем отложим на прямой АО отрезок ОА1, равный отрезку АО.
Таким образом, получили точку А1 симметричную точке А относительно прямой а.
На следующем рисунке точки B
и
B1
симметричны относительно прямой b,
точки C
и
C1
также симметричны относительно прямой b,
а вот точка D
симметрична
самой себе относительно прямой b. Точки Е и E1
не симметричны относительно прямой b,
так как прямая b
проходит не через середину отрезка EE1.
Точки Е и E1
не симметричны относительно прямой b,
так как прямая b
проходит не через середину отрезка EE1.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямую а называют осью симметрии фигуры.
Осевой симметрией обладает равнобедренный треугольник.
Он имеет одну ось симметрии, на которой расположена биссектриса, проведённая из вершины к основанию. То есть, если мы перегнём равнобедренный треугольник по оси симметрии, то каждая точка одной половины будет иметь симметричную ей точку на второй половине.
Равносторонний треугольник также обладает осевой симметрией и имеет три оси симметрии, на которых расположены биссектрисы углов треугольника.
Равнобедренная трапеция имеет ось симметрии, на которой
лежит прямая проходящая через середины её оснований.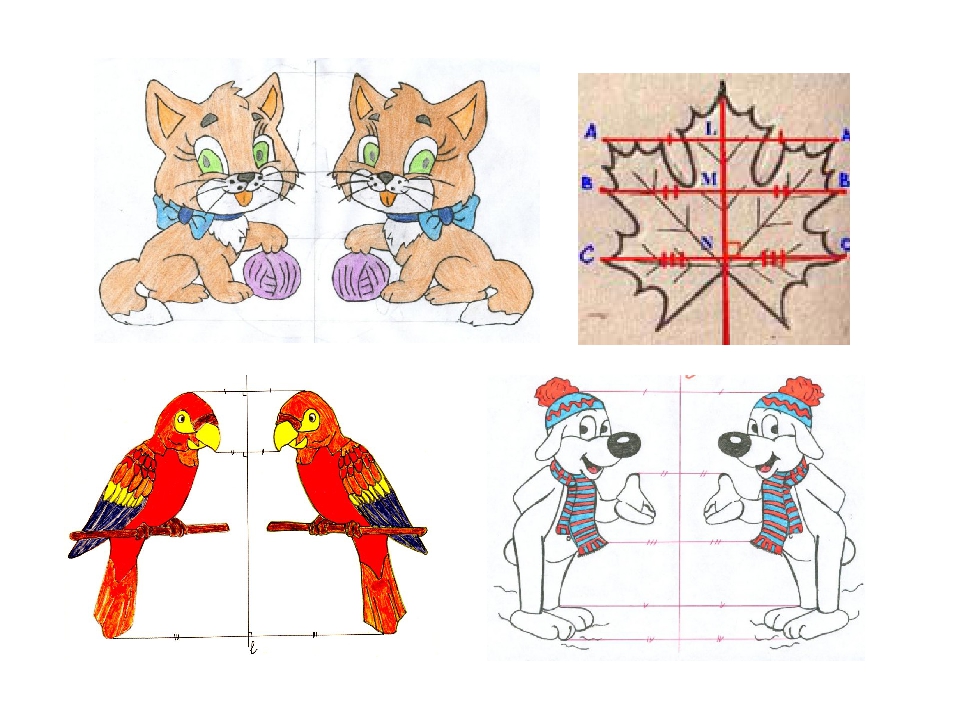
Прямоугольник имеет две оси симметрии, которые проходят через середины его противолежащих сторон.
Ромб также имеет две оси симметрии, на которых расположены его диагонали…
Квадрат имеет четыре оси симметрии, так как одновременно является и прямоугольником и ромбом.
А вот у окружности каждая прямая, проходящая через её центр, является осью симметрии. Так как таких прямых можно провести бесконечно много, то и осей симметрии у окружности бесконечно много.
Но есть и фигуры, у которых нет ни одной оси симметрии. Примерами таких фигур являются разносторонний треугольник. Или параллелограмм, который не является прямоугольником или ромбом.
Теперь поговорим о центральной симметрии, то есть симметрии относительно точки.
Точки А и A1 называются симметричными относительно точки О, если точка О – середина отрезка АА1.
Давайте найдём точку симметричную данной
относительно точки О.
Возьмём произвольные точки А и О. И проведём через них прямую АО. Затем на этой прямой отложим отрезок ОА1 равный отрезку АО.
Таким образом, мы получили точку А1 симметричную точке А относительно точки О.
Посмотрите на следующий рисунок.
Здесь точка B симметрична точке B1 относительно точки О. Точки C и C1 также симметричны относительно точки О. Точка О симметрична сама себе. А точки D и D1 не симметричны относительно точки О, так как отрезки DO и OD1 не равны.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Точку О называют центром симметрии фигуры.
Центральной симметрией обладает окружность.
Её центр является центром симметрии. То есть, для
любой точки окружности существует ей симметричная относительно центра.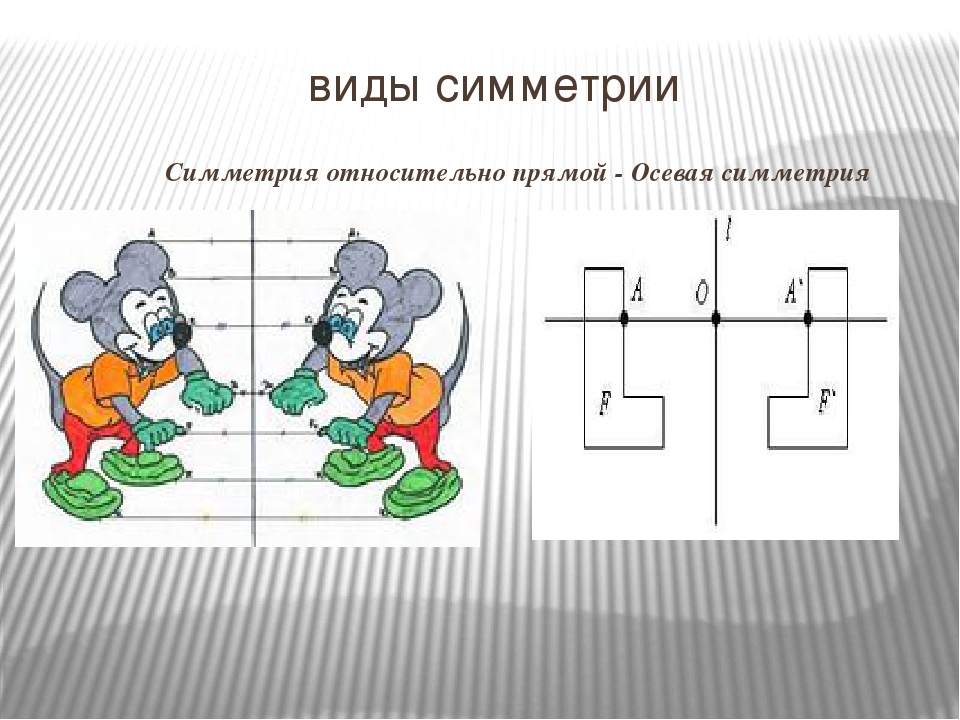
Параллелограмм также обладает центральной симметрией. Центром его симметрии является точка пересечения диагоналей.
Раз параллелограмм обладает центральной симметрией, то известные нам прямоугольник, ромб и квадрат также обладают центральной симметрией, центром которой является точка пересечения их диагоналей.
Центральной симметрией обладает и прямая, причём любая точка прямой является центром её симметрии.
Примером фигуры, не обладающей центральной симметрией, является произвольный треугольник.
А вот, например, такие фигуры, как прямоугольник, ромб, квадрат, окружность имеют обе симметрии (осевую и центральную).
Рисунок геометрических тел вращения, а именно конуса, цилиндра, шара, выполняется после того, как освоен рисунок куба. Сначала объёмные геометрические фигуры рисуют по отдельности, затем ставится натюрморт из геометрических тел. Любой рисунок начинающим следует вести исключительно с натуры. Модели гипсовых геометрических тел можно купить или изготовить самостоятельно из плотной бумаги или картона. Срисовывание с пособий, фотографий не имеет смысла и не приносит никакой пользы. Представленные мной примеры могут послужить в помощь для самостоятельного обучения или помочь при выполнении домашних заданий по рисунку, но всё же лучше всего заниматься с преподавателем. Если вы живёте в Москве, то у вас есть возможность брать индивидуальные уроки рисунка у автора статьи. Рисунок конусаКонус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа. Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.
Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания. Определив таким образом высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса. Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.
Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми. Следующий этап — построение эллипса. При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина. Чтобы передать объём в линии, ближнюю часть овала сделаем темнее.
После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба. Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее. Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали. Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму. Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы.
Рисунок цилиндраЦилиндр представляет собой простое тело вращения, у которого диаметр верхнего и нижнего основания равны, а плоскости оснований параллельны друг другу.
Последовательность работы над цилиндром такая же, как над рисунком конуса. Сначала намечаем место цилиндра в листе, сразу же легким штрихом выявляем объёмную форму. Затем работа ведётся последовательно, от большого к малому, от целого к детали. Старайтесь не давить излишне на карандаш, особенно при рисовании вспомогательных линий построения. Ластиком пользуйтесь как можно меньше. Если хотите поправить рисунок, то сначала обязательно нарисуйте правильную линию и только после того, как верная линия нарисована, можно стереть неверную. Когда стирают линию, а потом рисуют заново, то, как правило, повторяют уже сделанную ошибку. Сначала определяем высоту, а затем ширину цилиндра, насколько она меньше. Для сравнения высоты с шириной берите за основу расстояние между нижними краями эллипсов в центральной части цилиндра. После того, как найдены основные пропорции, рисуем осевую линию. Ось симметрии делит цилиндр ровно пополам. Построение эллипсов начинаем с верхнего. Нам хорошо видно, как он развёрнут. Нижний эллипс развёрнут больше, чем верхний, в соответствии с законами перспективы. Граница светотени у цилиндра проходит по вертикальной линии. Форма меняется плавно, поэтому границы размыты. Штрих кладём по форме, в вертикальном направлении. Удаляющиеся поверхности на свету становятся темнее, а в тени, наоборот, светлее. Верхнее основание оказывается в полутоне, если освещение преимущественно сбоку. Штрих этой горизонтальной плоскости аналогичен штриховке верхнего основания куба. Передний край падающей тени берёт своё начало от точки границы светотени в основании цилиндра, а дольний край тени начинается от аналогичной точки на невидимой стороне. На завершающем этапе работы уточняем форму штрихом в горизонтальном направлении.
Рисование шараГеометрическая форма шара самая простая из всех фигур, но для рисунка шар является самым сложным заданием. В первую очередь, начинающим сложно нарисовать ровный круг, трудно добиться плавных тональных переходов при штриховке, чтобы шар на рисунке не имел вмятин. Шар можно осветить естественным светом от окна или мягким светом с рассеивателем. Такой свет лучше, он не даёт резких теней.
При освещении лампой накаливания контраст сильнее, часто это приводит к тому, что начинающие изображают шар слишком тёмным, как будто он не из гипса, а из свинца.
Ниже представлен готовый рисунок шара. Изображения поэтапного ведения работы, построения теней, объяснения природы рефлексов появятся на сайте позже.
После того, как освоен рисунок геометрических тел по отдельности, можно приступить к рисованию группы из геометрических тел. Как правило, композиция включает в себя куб или параллелепипед, 1-2 тела вращения и шар. Рисунок кувшина также выполняется после того, как ученик умеет изображать простые геометрические формы. Разрешено копирование статей, только при наличии активной (кликабельной) ссылки на страницу-источник сайта Дениса Гаврилова gavrilovart.ru и при указании авторства. Ссылка должна находиться непосредственно рядом с материалом, должна быть видимой и прямой (без использования java-скриптов).
|
РОЛЬ ГЕОМЕТРИИ В ОРНАМЕНТЕ
РОЛЬ ГЕОМЕТРИИ В ОРНАМЕНТЕ
Куванова М. А. 1Пивоваров В.А. 1
А. 1Пивоваров В.А. 11МАОУ «Гимназия №1»
Дятел О.И. 11МАОУ *Гимназия №1*
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Человек всегда стремится украшать окружающее его пространство: цветами, колористическими решениями. И каждый раз люди пытаются придумать что-то новое, интересное. Все новое — хорошо забытое старое. Мы предлагаем обратить внимание на давно известное понятие в геометрии—ор-намент.
«А что такое орнамент?» — детский вопрос.Оглядись, посмотри, как красиво –Из орнаментов разных узорНа обоях, ковре. Белый с синимНа клеёнке штришками «забор»,
Разрисован и бабушкин фартук,На платочках — квадратиков ряд,И на мамином сереньком платьеНа кайме ярко стразы горят.Кружева на салфетках, накидкахСоставляют цветочный набор,А на стёкла зимою налипнетИз снежинок и льдинок узор.
Актуальность. Восхищаясь рукотворной красотой орнаментов, вопло-щенных в предметах декоратив-но-прикладного искусства, коврах, паркетах, гобеленах, вышивке и даже искусства уличного граффити — мы задумалисьо роли геометрии в создании этих произведений. Каждому человеку понятны принципы красоты. Но почему-то некоторым людям кажется, что они неспособны эту красоту воспроизвести. Математика может помочь в этом изящном искусстве и желании сделать красоту самому.
Объект исследования: орнаменты и узоры.
Предмет исследования: произведения искусства (картины, паркеты, ковры, часы), математика.
Цель исследования: изучение математических закономерностей, связанных с орнаментами и паркетами, а именно ответить на следующие вопросы:
-Какие геометрические преобразования лежат в основе создания таких орнаментов?
— Как построить измельчающие узоры?
Методы исследования:
— поисковый, аналитический, сравнения, наблюдения
Задачи:
Познакомиться с историей возникновения узоров.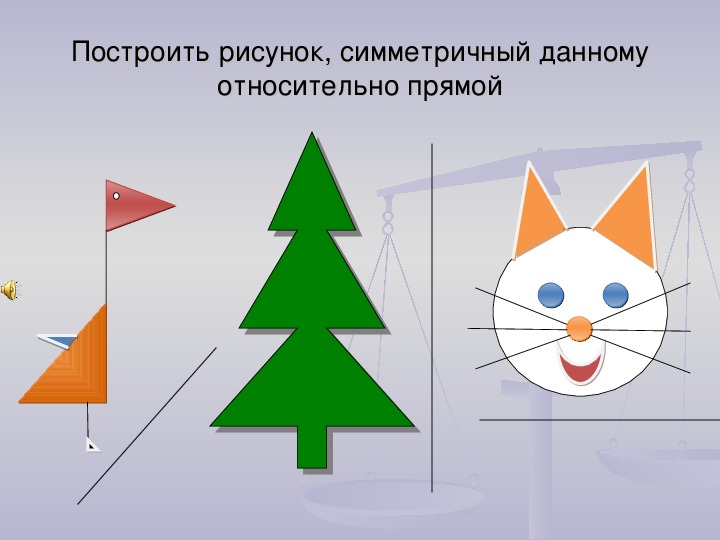
Применить знания на практике, создав орнамент на основе изученных закономерностей.
Показать важность математических закономерностей.
Гипотеза: предполагаем, что роль математики в построении узоров очень велика. Сложность узора зависит от теоретических знаний человека, который рисует его.
Глава 1.1 ГЕОМЕТРИЯ ОРНАМЕНТА
Орнамент (от лат. ornamentum — украшение) — это узор, состоящий из повторяющихся, ритмически упорядоченных элементов.
Орнамент предназначен для украшения различных предметов (посуды, мебели, текстильных изделий, оружия) и архитектурных сооружений
Приложение 1. Связанный с поверхностью, которую он украшает и зрительно организует, орнамент, как правило, выявляет и подчеркивает своим построением, формой и цветом архитектурные и конструктивные особенности предмета, природную красоту материала.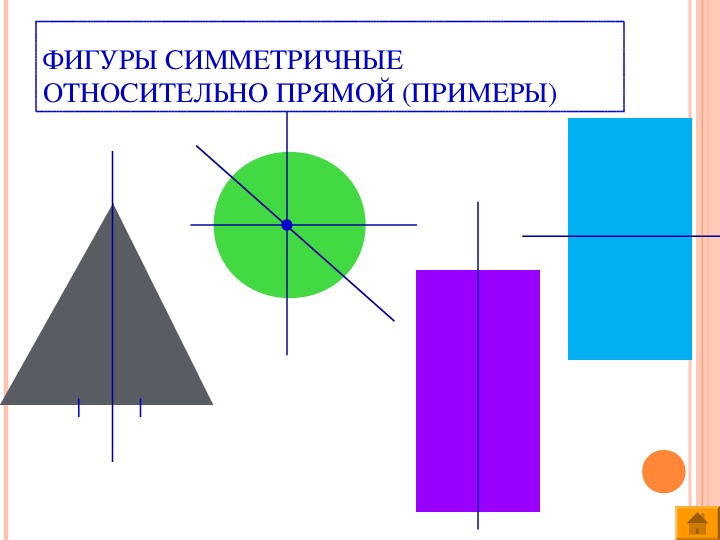
В построении орнамента используют главным образом принцип симметрии. Рассматривая разные композиции, легко увидеть, что орнамент можно продолжать в разные стороны, даже если его первоначальная композиция ограничена и замкнута.
В народном творчестве, где орнамент нашел наибольшее распространение, постепенно складывались устойчивые формы и принципы построения орнамента, во многом определившие национальные, художественные традиции разных народов.
Так, в орнаментах Древнего Египта наибольшее распространение нашли растительные мотивы, и среди них особенно часто встречались листья и цветы лотоса.Кажется, что египетский орнамент содержит какую-то тайну. Ведь египтяне так любили тайны. Над загадками их архитектуры и науки и сейчас бьются ученые-египтологи. Когда вы держите книгу обычным образом, то на рисунке вам бросаются в глаза нераспустившиеся бутоны.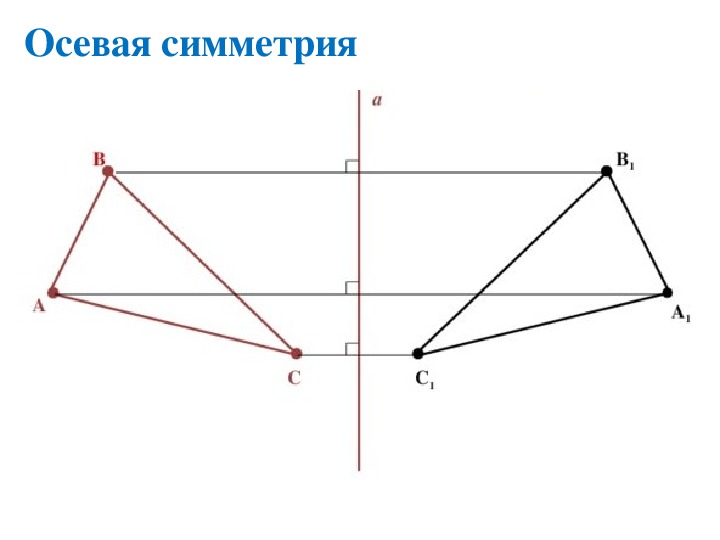 Но поверните книгу «вверх ногами», и тот же самый орнамент предстанет совсем другим: вы увидите лотос во всей красе, он широко раскинул свои великолепные лепестки, как бы вознаграждая нас за догадливость и умение видеть.Классическими стали наиболее распространенные древнегреческие орнаменты — меандр и акант -Приложение 1.
Но поверните книгу «вверх ногами», и тот же самый орнамент предстанет совсем другим: вы увидите лотос во всей красе, он широко раскинул свои великолепные лепестки, как бы вознаграждая нас за догадливость и умение видеть.Классическими стали наиболее распространенные древнегреческие орнаменты — меандр и акант -Приложение 1.
Слово «меандр» происходит от названия очень извилистой реки в Малой Азии. Ныне она называется Большой Мендерес. Орнамент меандр как будто повторяет излучины этой прихотливой реки. Акант — это род травянистого растения, распространенного в Средиземноморье. У него большие листья, красиво изогнутые стебли. В обоих этих орнаментах греки предстают перед нами прилежными учениками природы, которой они поклонялись. Они умели рассказать словами, вылепить из глины, вытесать из мрамора прекрасную сказку про каждый холм, каждую речку, каждый лист.
Не будет преувеличением сказать, что нигде орнаментальное искусство не достигло такого расцвета и совершенного воплощения, как на мусульманском Востоке.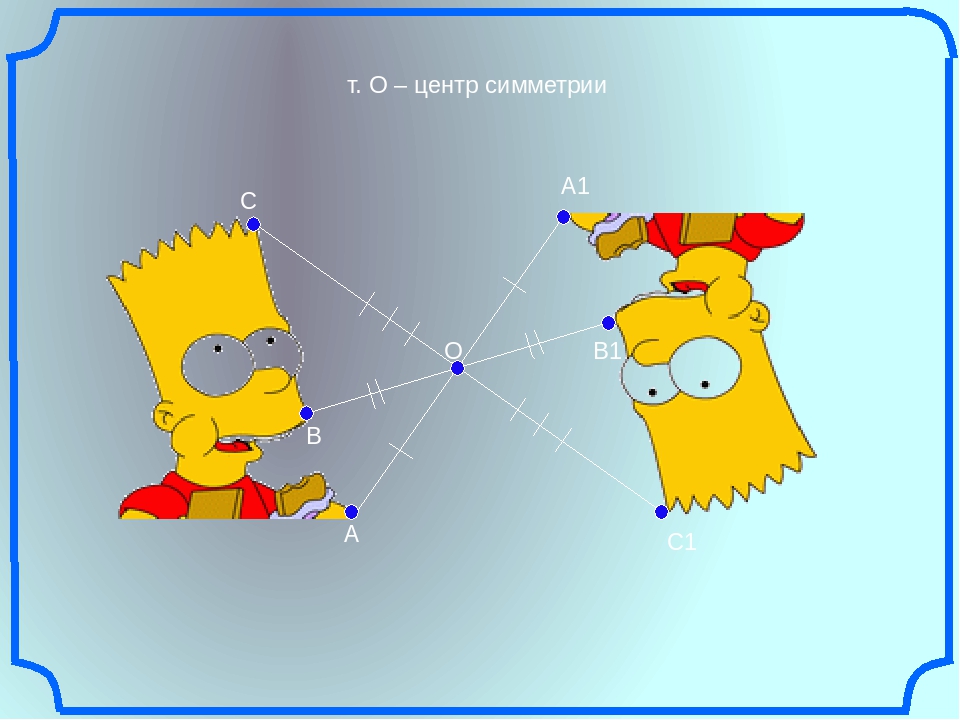 Для него характерно со-четание геометрических и растительных мотивов, так как Кора-ном было запрещено изображение людей и животных.
Для него характерно со-четание геометрических и растительных мотивов, так как Кора-ном было запрещено изображение людей и животных.
Впоследствии, распространившись по Европе, этот вид ор-намента получил название «арабеска» (от ит. arabesco — араб-ский). В исламских странах арабеску представлял узор. На первый взгляд мы видим повторения, диктуемые симметрией, но это только самые крупные элементы орнамента- Приложение 1.
Высокого развития орнамент достиг в средневековой Руси. Для русского орнамента характерны как геометрические и рас-тительные формы, так и изображения птиц, зверей, фантастиче-ских животных и человеческих фигур. Наиболее ярко русский орнамент выражен в резьбе по дереву и в вышивке. В плоском орнаменте одним из наиболее часто используемых мотивов яв-ляется так называемая плетенка — различного вида переплетения полосок типа лент, ремней, стеблей цветов-Приложение 1.
По сути, именно это открытие побудило в конце XIX века физиков и математиков подробнее изучить орнаменты (тогда и было дано точное математическое определение орнамента).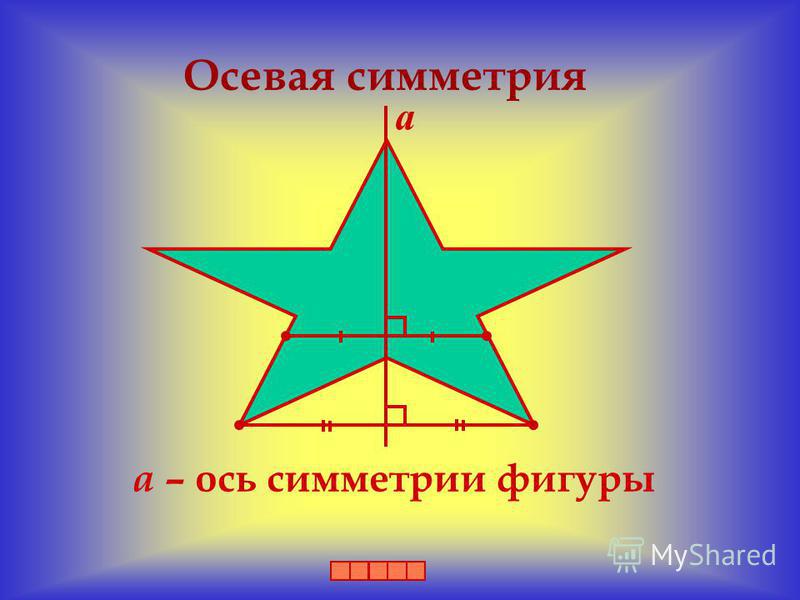
Глава 1.2 Геометрия в орнаменте
Анализируя некоторые орнаменты, можно наблюдать примеры применения в них геометрических построений. Например, деление окружности на равные части, сопряжения, применение циклоид, параллельных астроид и завитков.
Изучая орнаменты от самых древних до современных, можно заметить, что с течением времени менялось их содержание, но композиционный строй, его ритмическая основа оставались неизменными. В композиции орнамента присутствует математическая основа. Особую роль играют симметрия и разбиение плоскости на равные фигуры. Преобладающее большинство орнаментов построено на основе строгой математической логики.
Перечислим виды геометрических орнаментов, ограничиваясь главным и идя от простого к сложному. Приведенные нами примеры немногочисленны, и их легко умножить.
Прежде всего назовем точку, которая мало значит сама по себе, но при повторении дает декоративный эффект, успешно использованный в искусстве Ирана и в китайских изделиях Танского периода.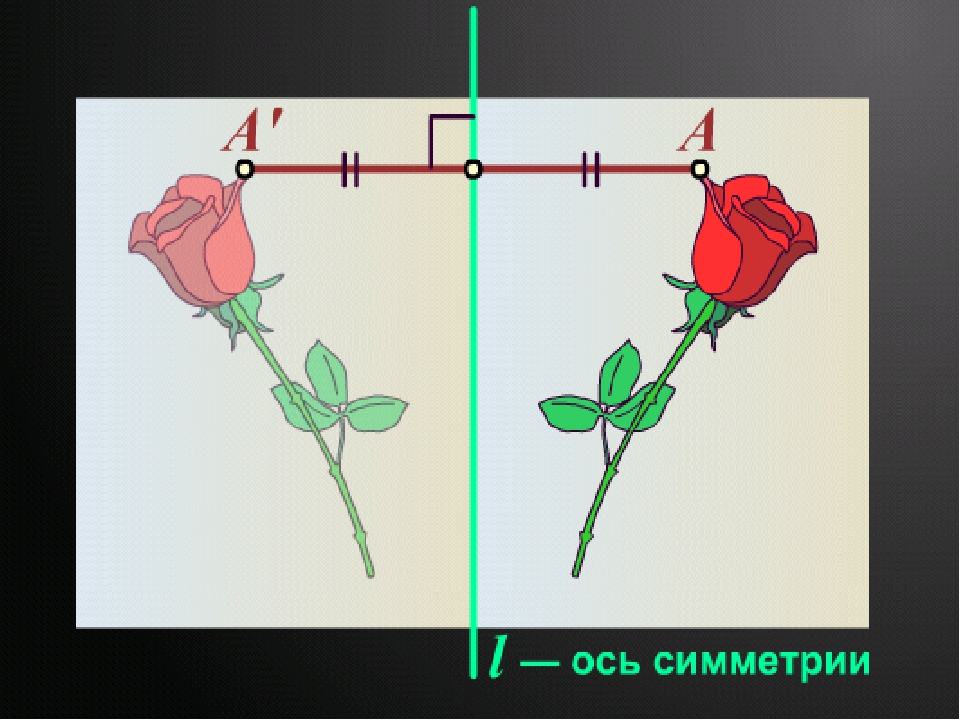
Затем идет линия или лента, широко применявшаяся для того, чтобы разграничить отдельные мотивы. Линию можно увидеть и в доисторических орнаментах и на греческих вазах (геометрический и классический стили).
Вязь характерна для искусства ислама, однако мы находим ее также в орнаментах самых разных стран. Вязь строится по принципу чередования зеркально — симметричных завитков. Напомним, что мотив плетенки встречается уже в древневосточном и греческом искусстве; в средние века вязь является излюбленным мотивом в книжной миниатюре, в некоторых романских орнаментах.
Меандр — изломанная под прямым углом лента — использовался и на греческих вазах геометрического стиля, и в искусстве Древней Мексики, и на
японских тканях. (Получил свое название от извилистой реки Меандр, в Малой Азии). Изгибы волнистых линий представляют собой тот же принцип меандра, только лишенный своей Геометрической четкости.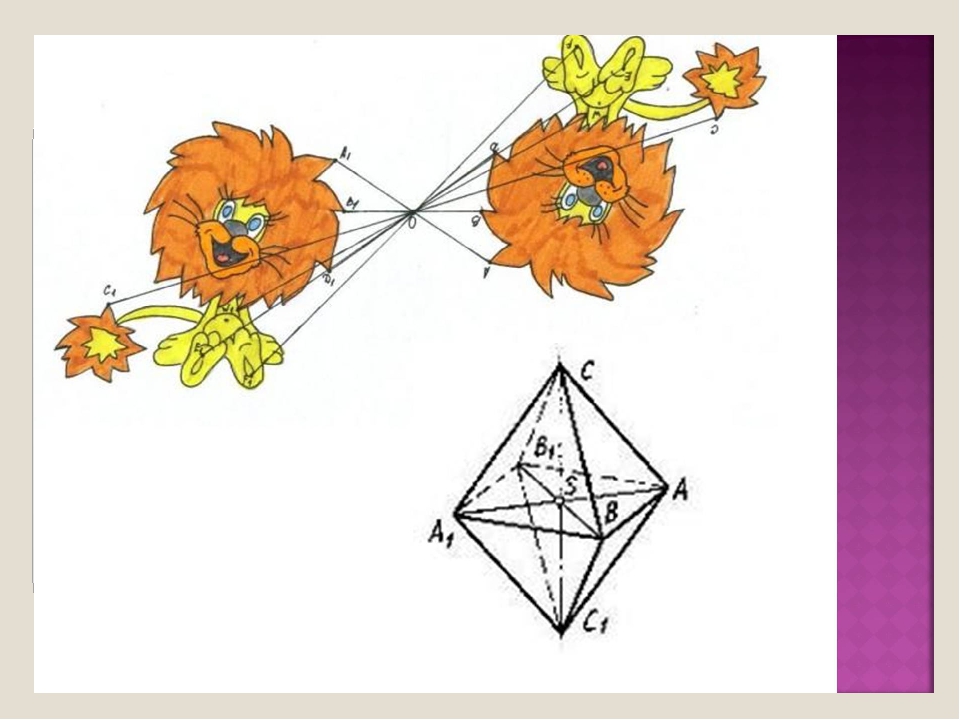
Квадрат, прежде всего, ограничивает поверхности, заполненные мотивами, как мы это видим, например, на кессонированных потолках эпохи Возрождения.
Ромб можно увидеть на множестве доисторической гончарной посуды и на китайских бронзовых изделиях периода Шан; он также служит для ограничения декорируемых поверхностей. То же можно сказать и о шашечном орнаменте, который широко используется в узорах тканей со времен Древнего Египта вплоть до современного искусства.
Треугольник служит орнаментальным мотивом для мозаичных полов и для тканей.
Шестиугольник и восьмиугольник, и их сочетания широко воспроизводились в декоративном искусстве стран ислама.
Среди кривых линий назовем в первую очередь синусоиду, волнообразную ленту, которая встречается как обрамление и в романском, и в китайском искусстве.
Спираль снискала большой успех и огромное распространение; она характерна для Эгейской, а затем и для микенской культур.
Часто и в самых разных странах применяется мотив круга, использовавшийся как собственно орнаментальный элемент, например на кипрских гончарных изделиях, так и для ограничения поверхности, заключающей в себе другие мотивы, как, например, на японских гербах.
Весьма своеобразными деталями некоторых орнаментов, например в Китае, являются элементы, называемые веревочными орнаментами. Они действительно напоминают фигуры, которые получаются при переплетении веревок. Некоторые из них представляют собой извилистое кольцо, обычно разделенное осью симметрии на две почти одинаковые части — левую и правую.
Линейные орнаменты называются бордюрами.
БОРДЮР – это периодически повторяющийся рисунок на длинной ленте. Бордюры используются в настенных росписях, в чугунном литье для оград, мостов, набережных. Рисунки в виде бордюров наносятся на ткани, мебель, обои и т.д.
Любой бордюр может быть совмещён сам с собой параллельным переносом. При рисовании бордюров кроме параллельного переноса используется симметрия относительно прямой, и центральная симметрия.
При рисовании бордюров кроме параллельного переноса используется симметрия относительно прямой, и центральная симметрия.
Математические принципы построения бордюров:
Для создания бордюров — линейных орнаментов — используются следующие преобразования:
а) параллельный перенос;
б) зеркальная (осевая) симметрия с вертикальной осью;
в) зеркальная (осевая) симметрия с горизонтальной осью;
г) поворотная (центральная) симметрия.
Всего существует семь типов симметрии бордюров:
а) В простейшем случае симметрия бордюра полностью исчерпывается переносной симметрией вдоль оси.
б) Бордюры обладают наряду с переносной также зеркальной симметрией. Здесь ось переноса является также осью симметрии.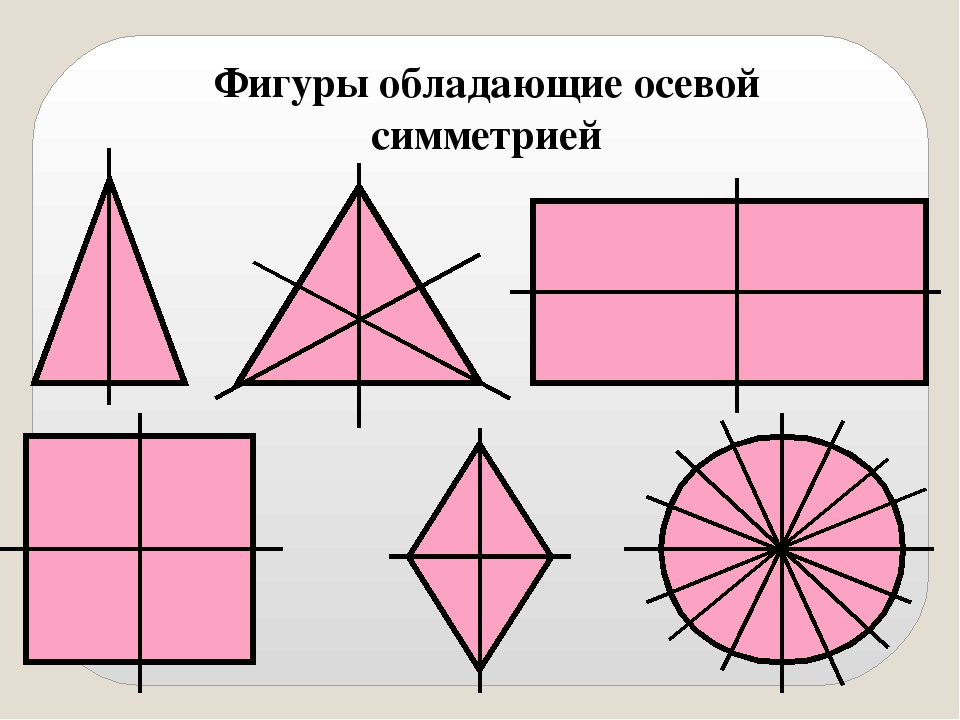
в) У бордюров ось переноса является осью скользящего отражения.
г) Бордюры имеют вертикальные оси симметрии. Эти оси изображены на рисунке в виде отрезков прямых, перпендикулярных к оси переноса.
д) Бордюры обладают переносной симметрией и поворотной симметрией (центральной).
е) Бордюры обладают переносной симметрией, центральной симметрией и осевой симметрией относительно вертикальной оси.
ж) Бордюры, основанные на комбинировании зеркальных отражений. Такие бордюры имеют наряду с вертикальной также горизонтальные оси симметрии.
Рисунок бордюра получается, когда мы начинаем геометрически перемещать его элемент. Любой бордюр может быть совмещен сам с собой параллельным переносом. При рисовании бордюров используются, кроме параллельного переноса, симметрия относительно прямой и центральная симметрия (симметрия относительно точки).
Для построения линейных орнаментов (бордюров) нужно начать с построения его ячейки: также придумывают узор (трафаретку), потом с помощью параллельного переноса переносят узор на длину вектора (направленного отрезка) влево или вправо во столько раз, сколько нужно.
Глава 1.3. Построение орнаментов на компьютере.
Основной принцип построения орнаментов в компьютерных программах – это отражение одного изображения в разные стороны.
«Рисунок» → «Отразить/повернуть» → «Отразить слева направо», «Отразить сверху вниз», «Повернуть на угол…»
Орнамент первого типа. Для его построения рисуем фрагмент, затем используем параллельный перенос.
Орнамент второго типа. Используем параллельный перенос и осевуюсимметрию (относительно горизонтальной оси).
Орнамент третьего типа.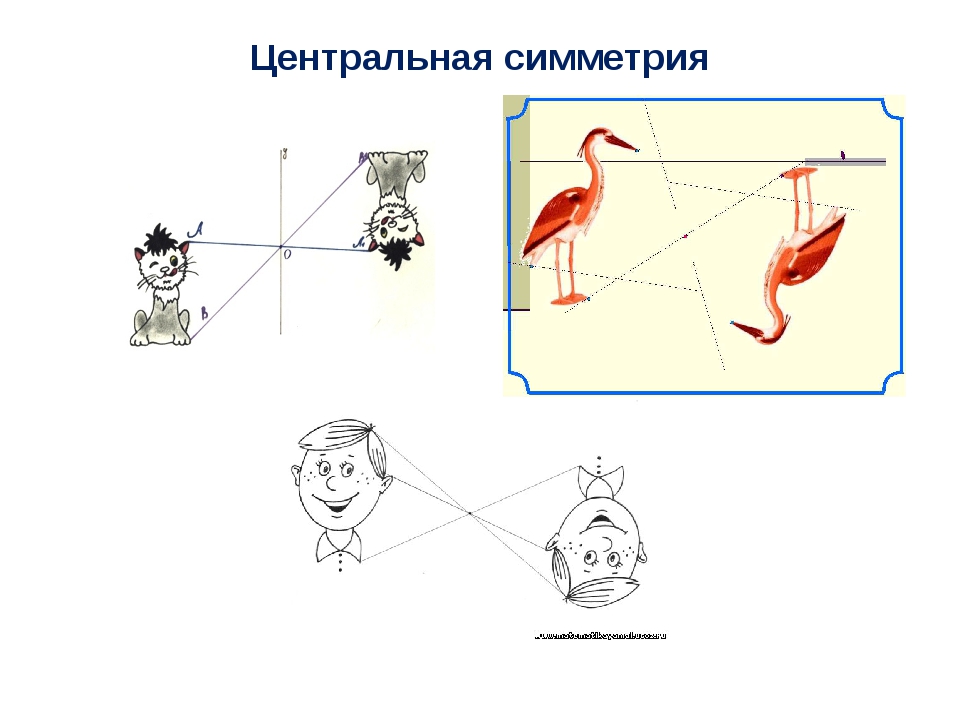 Используется композиция преобразований: осевая симметрия фрагмента относительно горизонтальной оси, параллельный перенос «нижней» части орнамента на вектор ā/2, параллельный перенос получившегося рисунка на вектор ā.
Используется композиция преобразований: осевая симметрия фрагмента относительно горизонтальной оси, параллельный перенос «нижней» части орнамента на вектор ā/2, параллельный перенос получившегося рисунка на вектор ā.
Орнамент четвёртого типа. Фрагмент отображается относительно вертикальной оси, затем осуществляется параллельный перенос получившегося рисунка.
Орнамент пятого типа. Композиция центральной симметрии и параллельного переноса.
Орнамент шестого типа. Композиция центральной симметрии, симметрии относительно вертикальной оси и параллельного переноса.
Орнамент седьмого типа. Композиция осевых симметрий относительно горизонтальной и вертикальной осей и параллельного переноса.
Глава 1.4 Виды орнаментов. Как создаются орнаменты.
По-характеру композиции и расположению на украшаемой поверхности орнамент может быть нескольких видов: ленточ-ным(его еще называют бордюром), сетчатым и розеточным.
Рассмотрим ленточные орнаменты — бордюры. Бордюром называют плоскую геометрическую фигуру, характеризующуюся векторами aи па (где n — целое число), при которых эта фигура переходит в себя, но не переходит в себя при парал-лельных переносах иного вида. Вектораназывают направляющим для бордюра.
Простейший бордюр построить очень просто: достаточно нарисовать какую-нибудь геометрическую фигуру и выполнить параллельный перенос на заданный вектор влево и вправо вдоль полосы. Такая «первоначальная фигура» называется фундаментальной областью бордюра.
Бордюры встречаются в разных местах: в настенных росписях, на лестничных переходах. Их можно увидеть в чугунном литье, которое используется в огра-дах парков, решетках мостов и набережных.
Доказано, что существует семь классов симметрии бордюров .
|
№ |
Свойства бордюров |
Пример |
|
|
Бордюры, которые не имеют иных симметрий, кроме параллельных переносов |
|
|
|
Бордюры, у которых фундаментальная область об-ладает центром симметрииО |
|
|
|
Бордюры, у которых фундаментальная область имеет ось симметрии, параллельную вектору а |
|
|
|
Бордюры, у которых фундаментальная область имеет ось симметрии, перпендикулярную вектору а |
|
|
|
Бордюры, у которых фундаментальная область име-ет одну ось симметрии, перпендикулярную вектору а, а дру-гую — параллельную вектору а |
|
|
|
Бордюры, имеющие такие оси симмет-рии, которых нет у фундаментальных областей |
|
|
|
Помимо бордюров художникам-орнаменталистам известен и другой вид орнамента — сетчатый.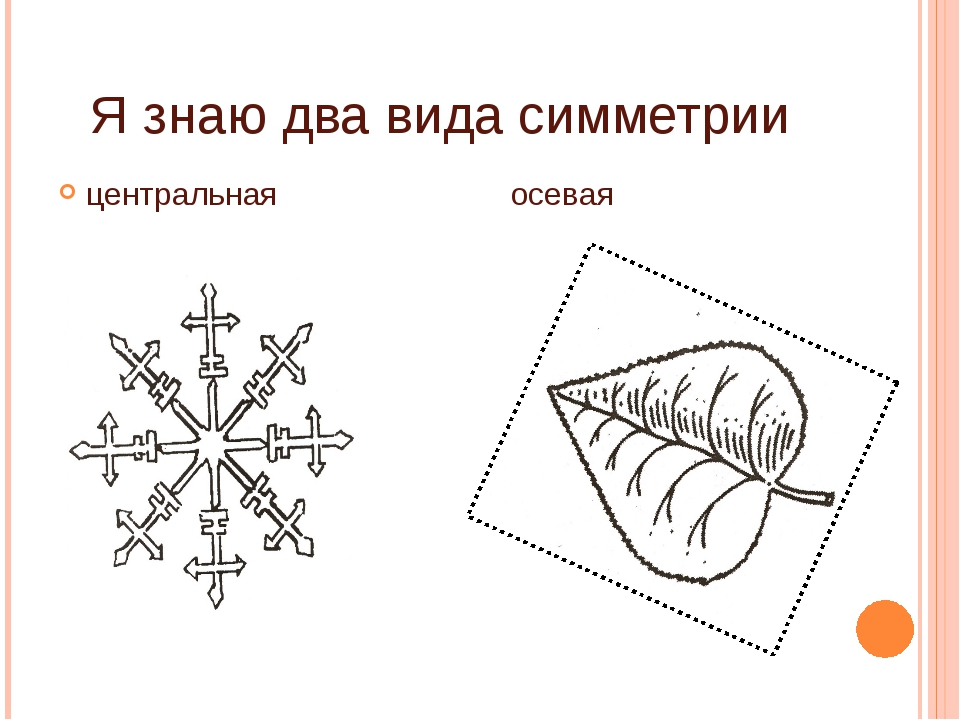 Он заполняет всю плоскую поверхность сплошным узором. Для построения такого орна-мента выделяют плоскую решетку, в которой одинаковые части повторяются в определенной геометрической последовательно-сти. Различают пять типов плоских решеток, каждая из кото-рых определяется двумя векторами а и b и углом п между ними. На рисунке показаны разные виды решеток: а) квадратная (а = b, а= 90°), б) прямоугольная (а ≠ b, а= 90°), в) гексальная (а = bа = 60°), д) ромбическая (a = b, а ≠90°, а ≠60°), г) косая (a ≠b, и a≠ 90°).
Он заполняет всю плоскую поверхность сплошным узором. Для построения такого орна-мента выделяют плоскую решетку, в которой одинаковые части повторяются в определенной геометрической последовательно-сти. Различают пять типов плоских решеток, каждая из кото-рых определяется двумя векторами а и b и углом п между ними. На рисунке показаны разные виды решеток: а) квадратная (а = b, а= 90°), б) прямоугольная (а ≠ b, а= 90°), в) гексальная (а = bа = 60°), д) ромбическая (a = b, а ≠90°, а ≠60°), г) косая (a ≠b, и a≠ 90°).
Вид орнамента определяется не только структурой его решетки, но и числом элементов его симметрии. Зная геометрические закономерности, можно и самим сконструировать интересный орнамент или определить те геометрические преобразования, которые положены в его основу. Приложение 2.
Чем больше элементов симметрии содержит элементарная ячейка, тем интереснее и красивее орнамент. Каж-дая прямая, проходящая через сторону квадрата, а также прямая в ячейке может стать осью симметрии орнамента. Кроме того, имеется девять точек (А, В, С, D, М, О, N, L, К), во-круг которых можно повернуть ячейку, чтобы образовать новую ячейку или совместить старую ячейку саму с собой.
Кроме того, имеется девять точек (А, В, С, D, М, О, N, L, К), во-круг которых можно повернуть ячейку, чтобы образовать новую ячейку или совместить старую ячейку саму с собой.
Помимо описанных видов орнамента в произведениях искусства встречается еще один. Такой орнамент замкнут и ограничен определенной геометрической формой (квадратом, ромбом, треугольником, кругом и др.). Орнамент, вписанный в круг или в правильный многоугольник, называется розеткой.
Глава 2. ГЕОМЕТРИЧЕСКИЕ ПАРКЕТЫ
Паркет (или мозаика) — бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек; но мы будем рассматривать как правильные, так и неправильные многоугольники.
Паркеты из одинаковых правильных многоугольников
Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Преобразуем отношение этих чисел:
Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Преобразуем отношение этих чисел:
Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.
Паркеты из разных правильных многоугольников
Паркеты из неправильных многоугольников
|
Параллелограмм |
|
|
Четырехугольник |
|
|
Произвольный треугольник |
|
|
Центрально-симметричный шестиугольник |
Паркеты из произвольных фигур
Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае — многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми).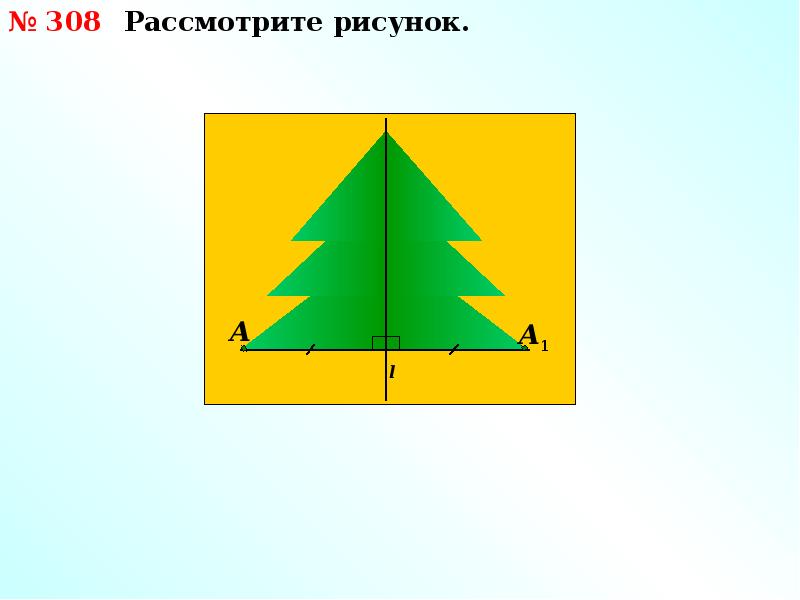 В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур. Рассмотрим способы построения нового паркета, исходя из этого «расширенного» определения. Итак, как нарисовать паркет? (некоторые из возможных способов)
В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур. Рассмотрим способы построения нового паркета, исходя из этого «расширенного» определения. Итак, как нарисовать паркет? (некоторые из возможных способов)
Способ первый. Паркеты, полученные заменой отрезков «квадратной» сетки некоторыми кривыми или ломаными.
Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки:
Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников:
Способ третий. Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить. В частном случае — накладываем друг на друга две (или более) сетки уже известных паркетов, смещая или поворачивая одну сетку относительно другой; фигуры, образовавшиеся при пересечении линий, считаем элементами паркета.Пример разбиения сетки из греческих крестов:
Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить. В частном случае — накладываем друг на друга две (или более) сетки уже известных паркетов, смещая или поворачивая одну сетку относительно другой; фигуры, образовавшиеся при пересечении линий, считаем элементами паркета.Пример разбиения сетки из греческих крестов:
Способ четвертый. Выбираем некоторую кривую или ломаную и начинаем ее переносить на некоторый вектор, поворачивать, отражать получившиеся кривые или ломаные размещаем на плоскости таким образом, чтобы они образовали замкнутые контуры (которые в дальнейшем будут рассматриваться как элементы паркета). Если рассматривать только незамкнутые кривые и ломаные, паркеты будут напоминать полученные способом №1.Для получения следующего паркета была взята дуга спирали, три раза повернута на 90°, а затем к получившейся фигуре был применен параллельный перенос.
А вот паркеты, полученные с помощью параллельного переноса звездчатых многоугольников:
Совмещая вершины звездчатых многоугольников, получаем паркеты, состоящие из правильных восьмиугольников, равнобедренных прямоугольных треугольников, а также из невыпуклых 16-угольников, напоминающих крест.
Глава 3.1 ГЕОМЕТРИЯ МОЗАИЧНОЙ РОЗЕТКИ. КОМПАС И КОЛЕСО
Четырехлучевую симметричную звезду часто называют компасом, поскольку этот знак напоминает и стрелку компаса, и маркировку карт, указывающую ориентацию относительно сторон света. Однако знаку этому намного больше лет, чем собственно компасу. Четырёхлучевые звезды были, вероятно, первыми геометрически построенными декоративными изображениями звезд, потому что построение такой звезды интуитивно доступно даже детям. Квадрат, крест, четырёхугольник легко преобразовываются в звезду, и четырехлучевые, четырехлепестковые изображения встречаются даже в доисторической пещерной графике.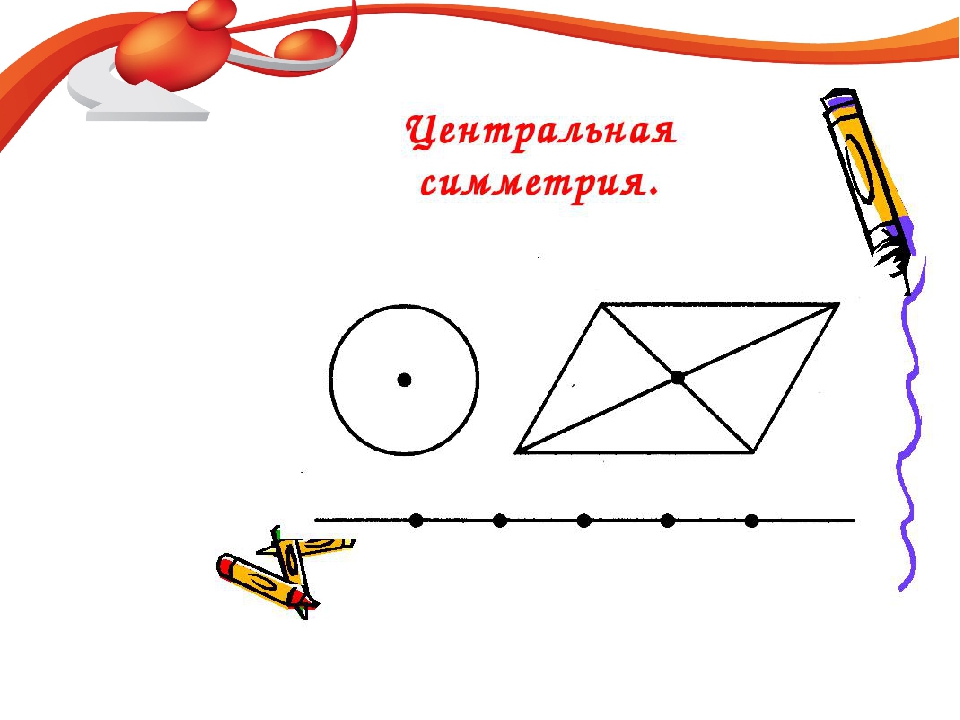 Дальнейшим естественным усложнением четырехлучевого знака является его удвоение и получение восьмилучевой звезды.
Дальнейшим естественным усложнением четырехлучевого знака является его удвоение и получение восьмилучевой звезды.
Лучи в круге или круг с лучами с центральной симметрией рисунка обычно восходят к сакральным изображениям солнца, особенно важным и значимым в древних религиях поклонения солнечным богам. Декоративные звезды как в орнаментах интерьера, так и в декоративной отделке предметов обихода, в одежде, в утвари и вооружении часто воспринимались (и воспринимаются) как защитный символ, оберег. И даже стремление современных дизайнеров и декораторов так или иначе использовать элементы типа розеток с симметрией из четного числа секторов в основе своей опирается на исторически заложенное позитивное восприятие таких образов.
Математика построения розетки-компаса предельно проста, концентрические круги и диаметральные лучи делят плоскость розетки на четыре, восемь, шестнадцать и тридцать две части.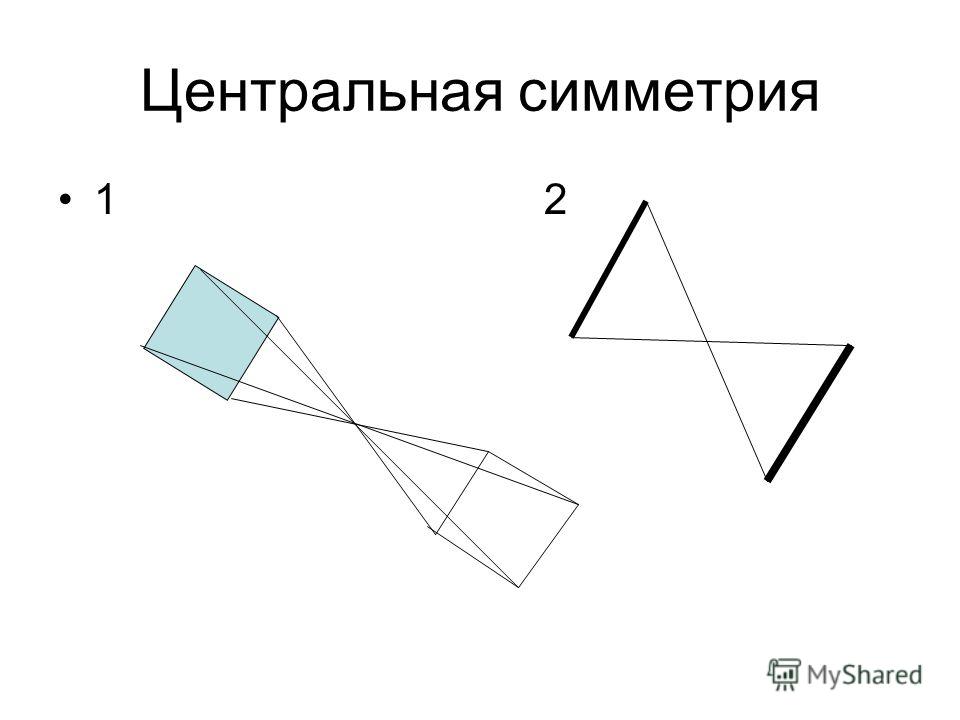 Лучи образуются за счет построения треугольников в кольцах рисунка. Количество колец и лучей, а также вытянутость лучей могут быть произвольными, однако следует помнить, что перегруженность рисунка мелкими деталями часто плохо воспринимается визуально, и в пропорциях построения лучей желательно следовать принципу золотого сечения, так как именно такое соотношение наиболее близко к природным, естественным пропорциям любых объектов.
Лучи образуются за счет построения треугольников в кольцах рисунка. Количество колец и лучей, а также вытянутость лучей могут быть произвольными, однако следует помнить, что перегруженность рисунка мелкими деталями часто плохо воспринимается визуально, и в пропорциях построения лучей желательно следовать принципу золотого сечения, так как именно такое соотношение наиболее близко к природным, естественным пропорциям любых объектов.
Геометрия мозаичной розетки
В зависимости от цветового решения розетки могут восприниматься по-разному. Если сделать акцент на лучевой структуре, то получится звезда, если подчеркнуть концентрические кольца рисунка, можно получить колесо.
|
Вариант цветового решения для мозаики из камня с преобладанием звездного мотива. |
|
|
Вариант цветового решения для паркетной розетки с акцентом на звездный рисунок. |
|
|
Вариант цветового решения с этнической гаммой и акцентом на мотив колеса и круга. |
Глава 3.2 ГЕОМЕТРИЯ МОЗАИЧНОЙ РОЗЕТКИ. ЗУБЧАТОЕ КОЛЕСО
Одним из самых древних видов мозаик с точки зрения рисунка были мощения полов и двориков в виде концентрических кругов. Первые мастера мозаичного дела выкладывали розетки из разноцветной гальки, но с развитием технологий камнеобработки для мозаик стали использоваться правильные квадраты и треугольники. Развитие математики и геометрии эпохи расцвета эллинских государств способствовало распространению знаний о законах симметрии и применению этих знаний в изобразительном искусстве, которое воспринималось неотъемлемой частью жизни и развития общества.
Геометрическое построение элементарных розеток — это разбиение круга на концентрические кольца и диаметральные сектора.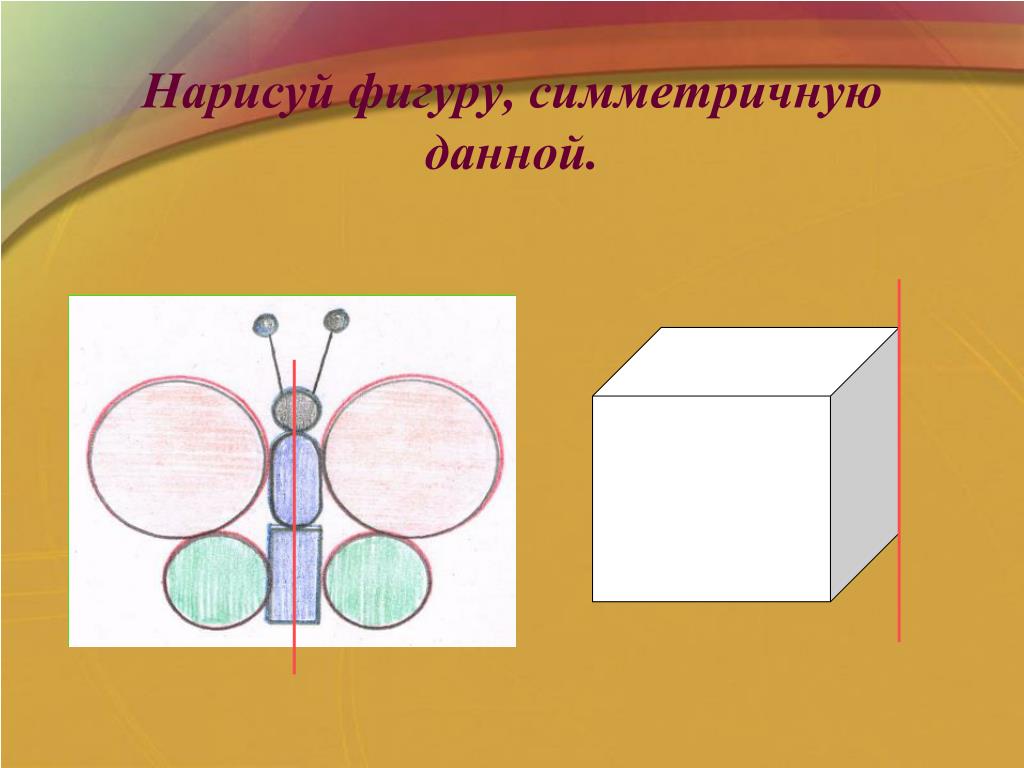 Рассмотрим простейший вариант создания такой розетки.
Рассмотрим простейший вариант создания такой розетки.
Цветовое решение для паркета Цветовое решение для дерева или камня
Начертив круг заданного радиуса, разобьём внутренний радиус на семь разных частей и проведем концентрические окружности. Внутренний круг разделим на восемь секторов, с углом 45 градусов. Следующие два круга делим ещё пополам, до 22,5 градусов, и последние деление проводим для последнего кольца. Третье и пятое кольцо от центра разбиваем на треугольники диагональю, проведенной в получившейся фигуре, которую можно принять за прямоугольник.
В результате получаем простой рисунок, все элементы которого могут быть представлены как примерно равные треугольники, прямоугольники, квадраты. Примерность эта важна для создания мозаик из простых каменных или деревянных деталей, не требующих сложных фигурных резов. Но в то же время рисунок даёт достаточно возможностей для фантазий и создания эффектных образов. В зависимости от цветовых вариаций рисунок розетки может напоминать зубчатое колесо или акцентировать внимание на лучах, исходящих из центра.
В зависимости от цветовых вариаций рисунок розетки может напоминать зубчатое колесо или акцентировать внимание на лучах, исходящих из центра.
Глава 3.3 МОЗАИКА ПЕНРОУЗА И ДРЕВНИЕ ИСЛАМСКИЕ УЗОРЫ
В 1973 году английский математик Роджер Пенроуз (RogerPenrose) создал особенную мозаику из геометрических фигур, которая так и стала называться – мозаикой Пенроуза. Мозаика Пенроуза представляет собой узор, собранный из многоугольных плиток двух определённых форм (немного различающихся ромбов). Ими можно замостить бесконечную плоскость без пробелов.
Мозаика Пенроуза в версии её создателя.
Она собрана из ромбов двух типов, один – с углом 72 градуса, другой – с углом 36 градусов. Картина получается симметричная, но не периодичная.Получающееся изображение выглядит так, будто является неким «ритмическим» орнаментом – картинкой, обладающей трансляционной симметрией.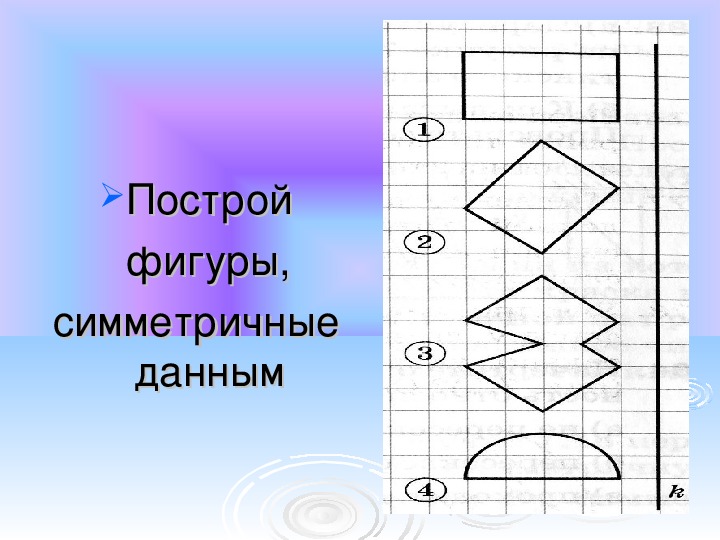 Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно «копировать» на плоскости, а затем совмещать эти «дубликаты» друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).
Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно «копировать» на плоскости, а затем совмещать эти «дубликаты» друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).
Однако, если присмотреться, можно узреть, что в узоре Пенроуза нет таких повторяющихся структур – он апериодичен. Но дело отнюдь не в оптическом обмане, а в том, что мозаика не хаотична: она обладает вращательной симметрией пятого порядка.
Это значит, что изображение можно поворачивать на минимальный угол, равный 360 / n градусам, где n – порядок симметрии, в данном случае n = 5. Следовательно, угол поворота, который ничего не меняет, должен быть кратен 360 / 5 = 72 градусам.
Примерно десятилетие выдумка Пенроуза считалась не более чем милой математической абстракцией. Однако в 1984 году Дэн Шехтман (DanShechtman), профессор израильского технологического института (Technion), занимаясь изучением строения алюминиево-магниевого сплава, обнаружил, что на атомной решётке этого вещества происходит дифракция.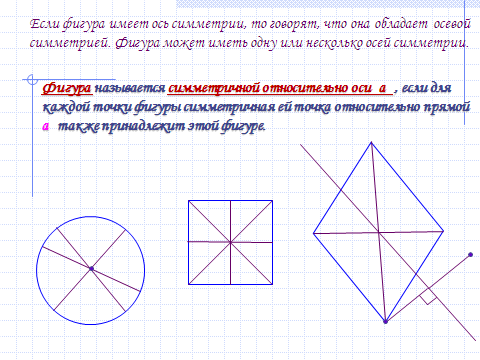
Предыдущие представления, существовавшие в физике твёрдого тела, исключали такую возможность: структура дифракционной картины обладает симметрией пятого порядка. Её части нельзя совмещать параллельным переносом, а значит, это вовсе никакой не кристалл. Но дифракция характерна как раз для кристаллической решётки! Учёные договорились о том, что данный вариант будет назваться квазикристаллами – чем-то вроде особого состояния вещества. Ну а вся красота открытия в том, что для него уже давно была готова математическая модель — мозаика Пенроуза.
А совсем недавно стало понятно, что этой математической конструкции намного больше лет, чем можно было себе представить. В 2007 году Питер Лу (Peter J.Lu), физик из Гарварда (HarvardUniversity) за компанию с другим физиком — Полом Стейнхардтом (Paul J. Steinhardt), но из Принстона (PrincetonUniversity), — опубликовал в Science статью, посвящённую мозаикам Пенроуза .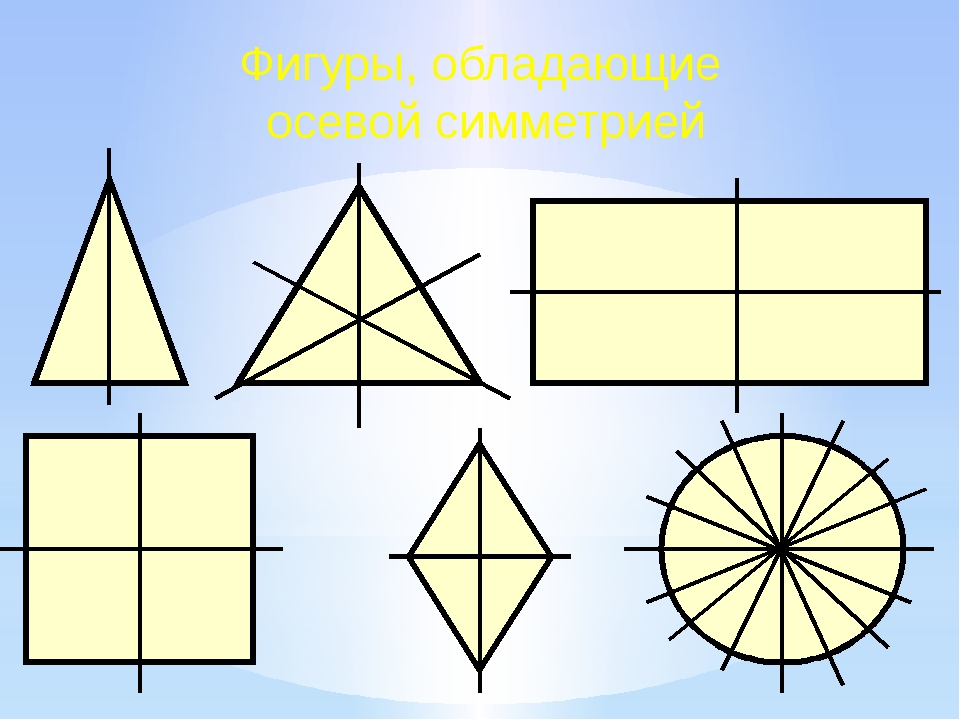 Казалось бы, неожиданного тут немного: открытие квазикристаллов привлекло живой интерес к данной теме, что привело к появлению кучи публикаций в научной прессе.
Казалось бы, неожиданного тут немного: открытие квазикристаллов привлекло живой интерес к данной теме, что привело к появлению кучи публикаций в научной прессе.
Однако изюминка работы в том, что она посвящена далеко не современной науке. Да и вообще — не науке. Питер Лу обратил внимание на узоры, покрывающие мечети в Азии, построенные ещё в Средневековье. Эти легко узнаваемые рисунки сделаны из мозаичной плитки. Они называются гирихи (от арабского слова «узел») и представляют собой геометрический орнамент, характерный для исламского искусства и состоящий из многоугольных фигур.
Образец выкладки плитки, показанный в арабском манускрипте XV века.
Цветами исследователи выделили повторяющиеся области. На основе этих пяти элементов выстроены все геометрические узоры средневековых арабских мастеров. Повторяющиеся элементы не обязательно совпадают с границами плиток.
В исламском орнаменте выделяют два стиля: геометрический – гирих, и растительный – ислими. Гирих (перс.) – сложный геометрический орнамент, составленный из стилизованных в прямоугольные и полигональные фигуры линий. В большинстве случаев используется для внешнего оформления мечетей и книг в крупном издании. Ислими (перс.) – вид орнамента, построенного на соединении вьюнка и спирали. Воплощает в стилизованной или натуралистической форме идею непрерывно развивающегося цветущего лиственного побега и включает в себя бесконечное разнообразие вариантов. Наибольшее распространение он получил в одежде, книгах, внутренней отделке мечетей, посуде.
Гирих (перс.) – сложный геометрический орнамент, составленный из стилизованных в прямоугольные и полигональные фигуры линий. В большинстве случаев используется для внешнего оформления мечетей и книг в крупном издании. Ислими (перс.) – вид орнамента, построенного на соединении вьюнка и спирали. Воплощает в стилизованной или натуралистической форме идею непрерывно развивающегося цветущего лиственного побега и включает в себя бесконечное разнообразие вариантов. Наибольшее распространение он получил в одежде, книгах, внутренней отделке мечетей, посуде.
Обложка Корана 1306-1315 годов и прорисовка геометрических фрагментов, на которых основан узор. Этот и следующий примеры не соответствуют решёткам Пенроуза, но обладают вращательной симметрией пятого порядка
До открытия Питера Лу считалось, что древние архитекторы создавали узоры гириха c помощью линейки и циркуля (если вообще не по наитию). Однако пару лет назад, находясь во время путешествия в Узбекистане, Лу заинтересовался узорами мозаик, украшавшими местную средневековую архитектуру, и приметил в них что-то знакомое.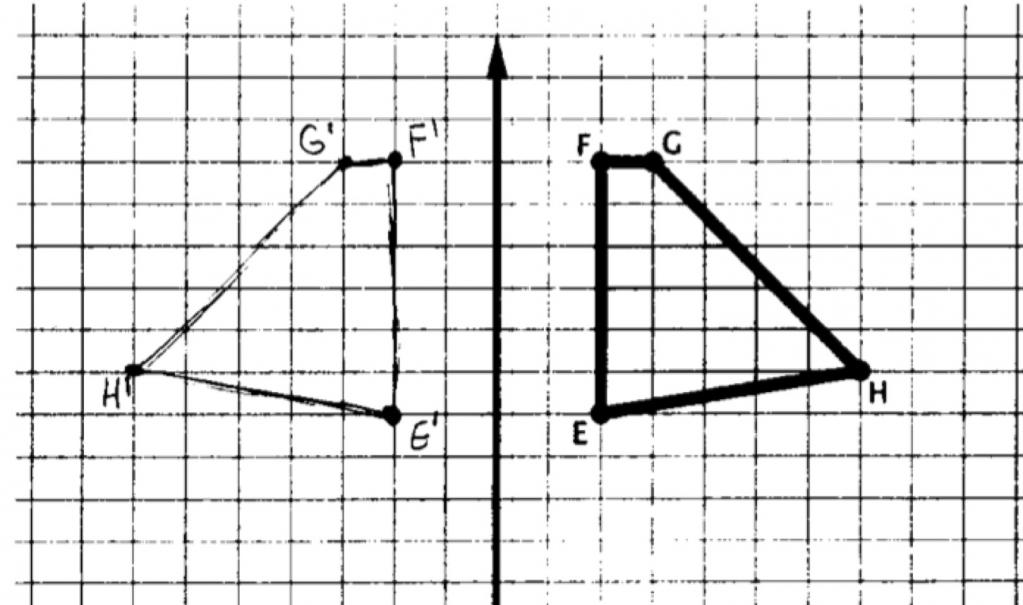 Вернувшись в Гарвард, учёный стал рассматривать аналогичные мотивы в мозаиках на стенах средневековых построек Афганистана, Ирана, Ирака и Турции.
Вернувшись в Гарвард, учёный стал рассматривать аналогичные мотивы в мозаиках на стенах средневековых построек Афганистана, Ирана, Ирака и Турции.
Этот образец датирован более поздним периодом – 1622 год (индийская мечеть). Глядя на него и прорисовку его структуры, нельзя не восхититься трудолюбию исследователей. И, конечно же, самих мастеров.Питер Лу обнаружил, что геометрические схемы гирихов практически одинаковы, и смог выделить основные элементы, использовавшихся во всех геометрических орнаментах. Кроме того, он нашёл чертежи этих изображений в старинных манускриптах, которыми древние художники пользовались в качестве своеобразной шпаргалки по украшению стен.Для создания этих узоров применяли не простые, случайно придуманные контуры, а фигуры, которые были расположены в определённом порядке. Древние узоры оказались точными построениями мозаик Пенроуза.
На этих снимках выделены одинаковые области, хотя это и фотографии из самых разных мечетей
Образцом почти идеальной квазикристаллической структуры исследователи посчитали святилище имама Дарб-и в иранском городе Исфахане, датируемое 1453 годом.
Портал святилища имама Дарб-и в Исфахане (Иран). Здесь друг на друга наложены сразу две системы гирихов.
Колонна внутреннего двора мечети в Турции (около 1200 года)и стены медресе в Иране (1219 год). Это ранние произведения, и в них используется всего два структурных элемента, найденных Лу.
Глава 3.4 ПОСТРОЕНИЕ МОЗАИК В СТИЛЕ МОРИСА ЭШЕРА
В геометрии под мозаикой (паркетом) понимают заполнение плоскости одинаковыми фигурами (элементами мозаики), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда мозаикой называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками). Обычный тетрадный лист в клеточку представляет собой простейшую геометрическую мозаику. Элементом здесь является квадрат. Элементами мозаики могут быть также равносторонний треугольник, правильный шестиугольник, произвольный параллелограмм, произвольный четырехугольник. Можно придумать сотни, тысячи разных элементов паркетов- Приложение 3.
Можно придумать сотни, тысячи разных элементов паркетов- Приложение 3.
Придуманы мозаики, у которых несколько элементов образуют фигуру, подобную элементу мозаики. Примеры таких паркетов:
Мозаика-паркет, элементами которой являются одинаковые пятиугольники с углами 90°, 120°, 60°, 240° и 30°, которые получились разбиением правильного шестиугольника. Из этих пятиугольников образованы фигуры.
Всего существует 17 видов симметрии сетчатых орнаментов – Приложение 4.
Мозаики являются прекрасным материалом для интересного и содержательного изучения геометрии и некоторых закономерностей расположения фигур на плоскости. Визуальное представление и необходимость решения с виду простой задачи занимает как детей, так и взрослых. Составление своих рисунков мозаик может стать как профессиональной задачей дизайнера, так и уроком для школьников.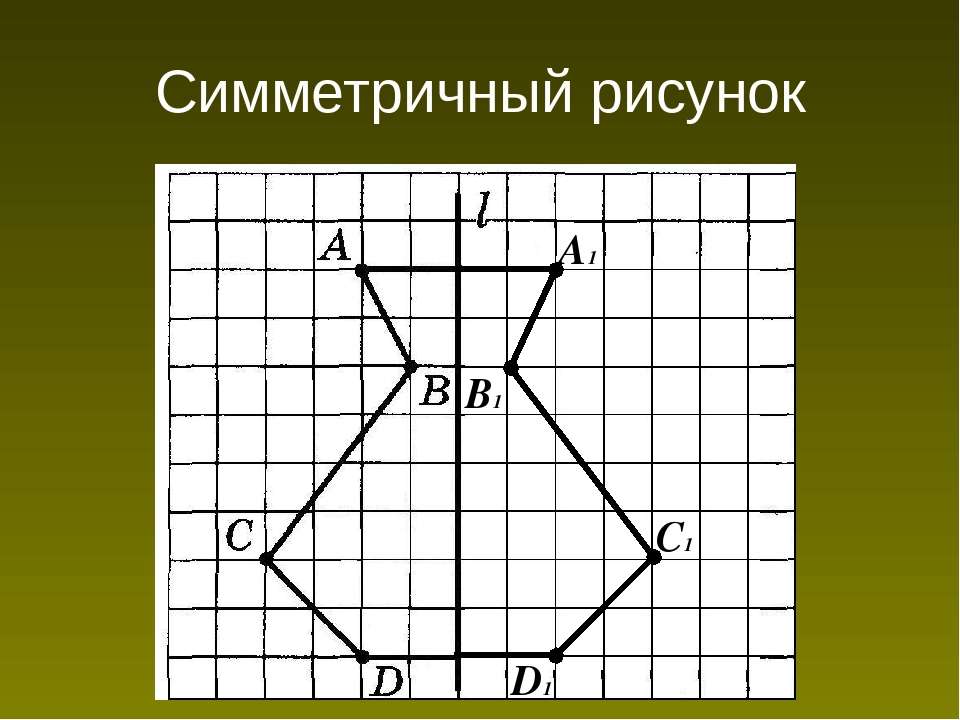
Одни из самых знаменитых рисунков мозаик придумал голландский художник Морис Эшер. Элементами паркета у него служили фигуры животных, птиц, рептилий, находящиеся в определенном порядке по отношению друг к другу.
На рисунках Приложения 5 представлено несколько фигур, получить мозаику из которых можно геометрической операцией параллельного переноса. На деле это означает, что фигурка смещается на некоторое расстояние и как бы вкладывается в предыдущую, не меняя своего положения. Если в качестве меры расстояния взять 1 клеточку, то рассчитав, на какое количество клеточек нужно смещать фигурку вверх и вправо, получим два числа, определяющих вектор перемещения. Для школьников интересно проследить связь между параллельными переносами и векторами и возможность разложения каждого вектора полученного векторного пространства по двум базисным векторам. Для взрослых — поиграться с неправильным копированием образца.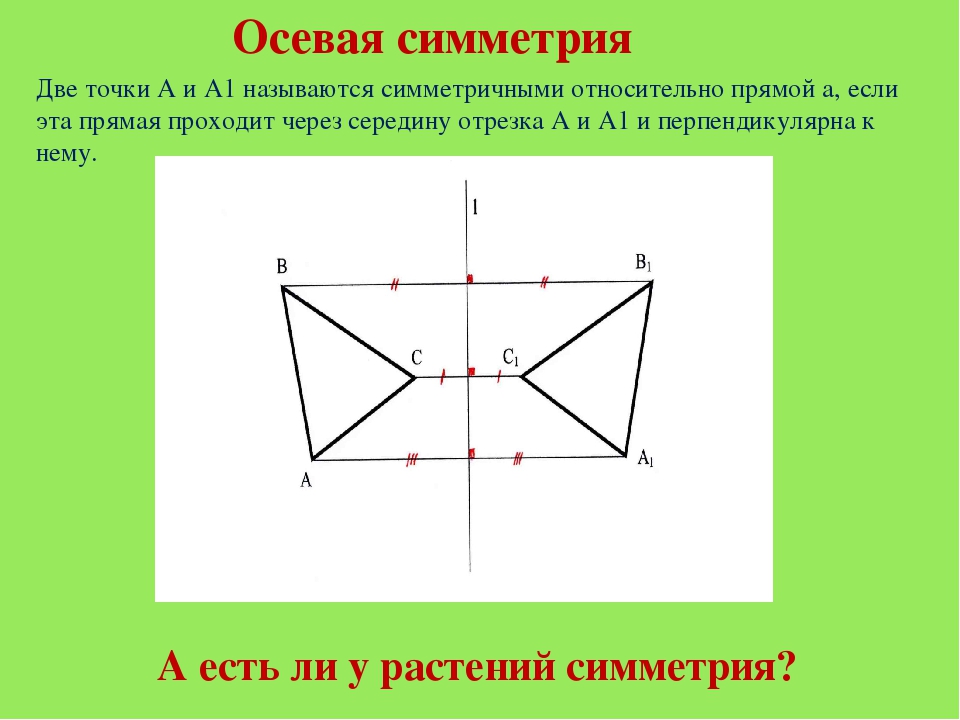 Изменение вектора может привести к получению интересных мозаичных рисунков.
Изменение вектора может привести к получению интересных мозаичных рисунков.
Общий принцип построения мозаик из сложных фигур (рисунков животных, растений, объектов с криволинейными формами) с использованием различных видов симметрии можно описать как постепенный переход от простых фигур » по тетрадным клеточкам» к более сложным. Начав с простых квадратов и четырехугольников, постепенно усложняя и развивая фигуры, получаем сначала примитивное схематичное изображение, затем добавлением деталей и скруглением форм получаем детализированное изображение со сглаженным контуром- Приложение 6.
Как пример — мозаики, разработанные в таком же стиле. Автор рисунков — А. Цукарь- Приложение 7.
Мозаики, подобные приведенным, универсальны по применению. Разработка мозаичных элементов может отталкиваться не от форм живых существ, а от различных объектов символики, техногенных и урбанистических форм, пиктограмм и прочего.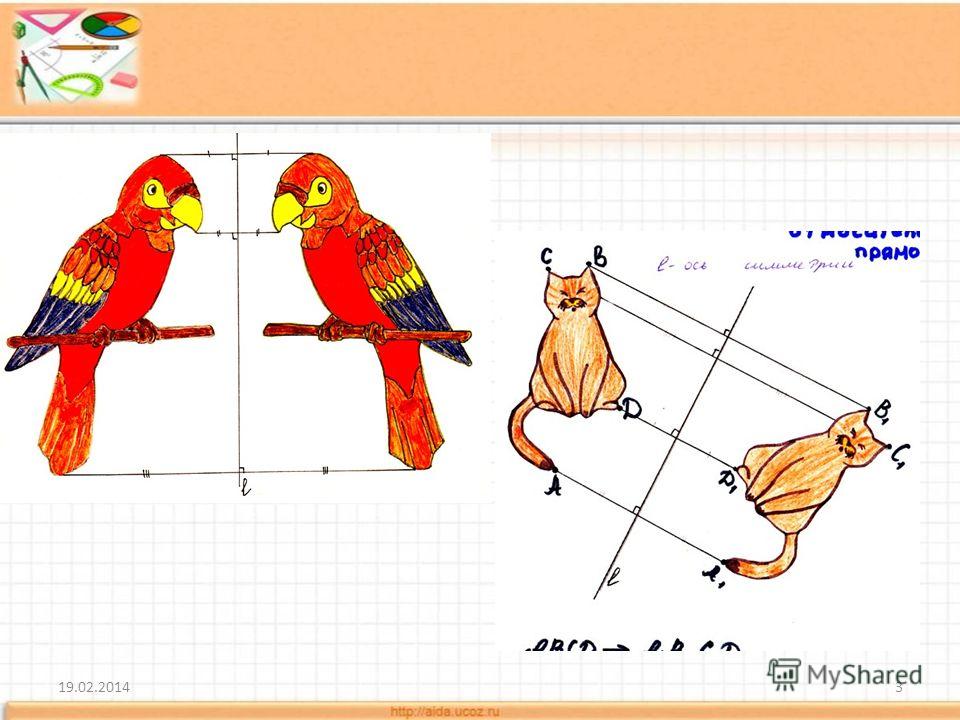 Одним из факторовпопулярности мозаик Эшера является их способность заставлять зрителя погружаться в изучение подробностей рисунка — от мелких деталей к крупным, от восприятия в целом к сосредоточению на одном элементе. Разглядывание мозаик — отличный способ расслабления и отдыха, приведения мыслей в порядок, и даже медитации. Декорирование пространства мозаикой собственной разработки — это и дополнительные возможности формирования позитивного настроения путем использования конкретных образов, формирующих положительное впечатление.
Одним из факторовпопулярности мозаик Эшера является их способность заставлять зрителя погружаться в изучение подробностей рисунка — от мелких деталей к крупным, от восприятия в целом к сосредоточению на одном элементе. Разглядывание мозаик — отличный способ расслабления и отдыха, приведения мыслей в порядок, и даже медитации. Декорирование пространства мозаикой собственной разработки — это и дополнительные возможности формирования позитивного настроения путем использования конкретных образов, формирующих положительное впечатление.
Приложение 8.
Вывод
Орнамент — это узор, состоящий из повторяющихся, ритмически упорядоченных элементов. В построении орнамента используют главным образом принцип симметрии.В основе узоров лежат основные геометрические преобразования т.к. симметрии, разные геометрические фигуры.
Роль математики в построение узоров на улице (стрит-арт) очень важна. Если не знать основные математические закономерности, то построить узор будет практически нереально.
Если не знать основные математические закономерности, то построить узор будет практически нереально.
Заключение
Проведённая работа помогла изучить и систематизировать процедуру построения орнаментов (бордюров), которую коротко можно описать в виде следующего алгоритма:
1. Рисуется фрагмент орнамента. Это может быть законченный элемент в виде цветка, ветки, завитка, или его часть — половина, четверть. Например, половина бабочки или четверть ромба.
2. Полученный фрагмент отображают с помощью одного из следующих геометрических преобразований: осевая симметрия, центральная симметрия, параллельный перенос. Возможно использование композиции нескольких преобразований.
3. Полученный более сложный фрагмент с помощью параллельного переноса «распространяют» на необходимую длину.
Семь основных способов построения бордюров позволяют получить несколько различных композиций, основанных на использовании одного фрагмента, создавая тем самым неограниченные просторы для творчества.
Использование орнаментов в быту, различных ремёслах, живописи, архитектуре делает окружающие нас предметы ярче и выразительнее, расцвечивает их новыми красками, привлекает внимание, давая повод для осмысления и понимания красоты и гармонии. Кроме бордюров существуют и другие виды орнаментов, но это — тема для новых исследовательских работ.
А эта работа увлекла нас настолько, что захотелось создавать новые и новые орнаменты. И вот что у нас получилось.
Созданные нами орнаменты:
Продолжение в приложении 9.
Список литературы
А.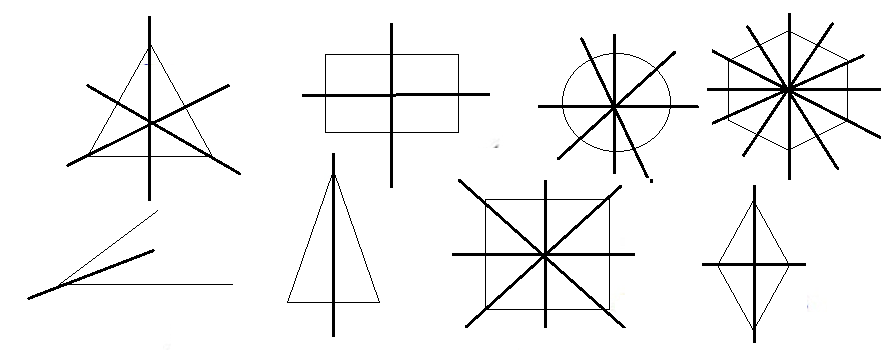 Н.Колмогоров. Паркеты из правильных многоугольников. Журнал «Квант» №3, 1970 г.
Н.Колмогоров. Паркеты из правильных многоугольников. Журнал «Квант» №3, 1970 г.
П.И.Совертков и др. Геометрический паркет на экране компьютера журнал «Информатика и образование, №9 за 2002 г.
http://otherreferats.allbest.ru/culture/00165702_0.html
Приложение 1
а) б)
в) г)
д)
Орнамент в украшении ванной Кувшин с мозаикой
Орнамент в украшении оружия
Мозаика на тарелке Мозаика на шкафу Мозаика на сундуке
в стиле барокко
Стол в технике мозаика Тарелки в технике мозаика
Мозаика потолка мечети Мозаика стен мечети
Диван и столик.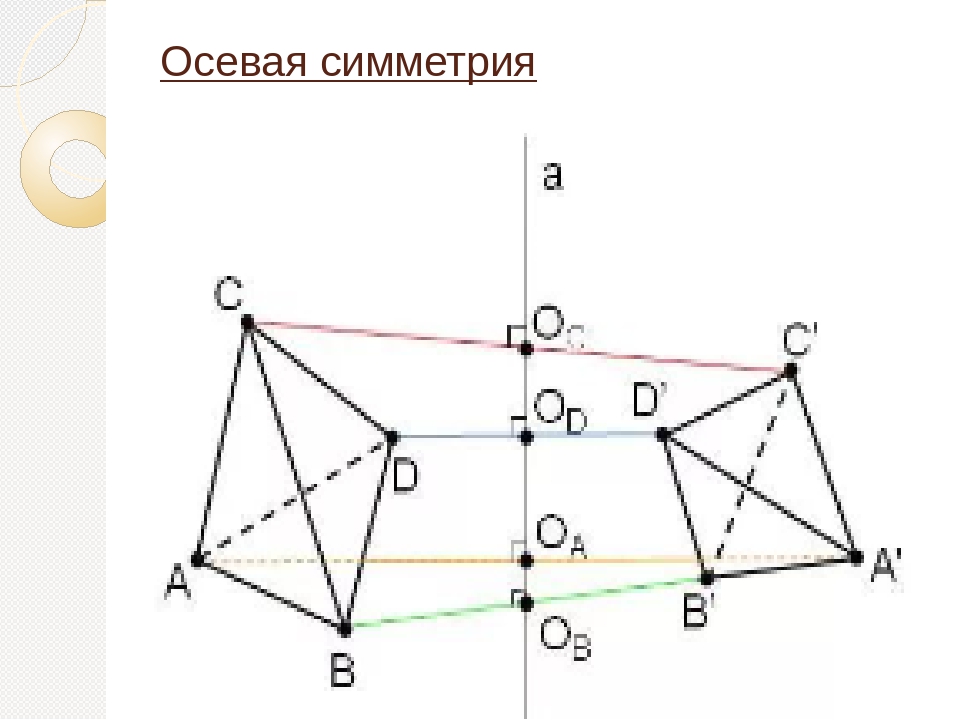 Орнамент. Комод в стиле рококо.
Орнамент. Комод в стиле рококо.
Орнамент в одежде Орнамент на рубашке
Приложение 2
Приложение 3Приложение 4
Приложение 5
Приложение 6
Приложение 7
Приложение 8
Проект мозаики Мориса Эшера в смальте
Настенное панно из мозаики по картине М. Эшера «Птицы»
Приложение 9
Также мы создали орнаменты в других изделиях
Деревянные дощечки с орнаментальной росписью Самовар, вырезанный из дерева, с орнаментомПросмотров работы: 3747
Красивый геометрический арт-проект с симметрией
Сегодняшний геометрический арт-проект — это хранитель, поскольку они настолько красивы, что вы захотите отобразить их, когда закончите! В этом красочном математическом арт-проекте мы будем использовать симметрию и оси для создания прекрасных бумажных плиток!
Этот пост содержит партнерские ссылки.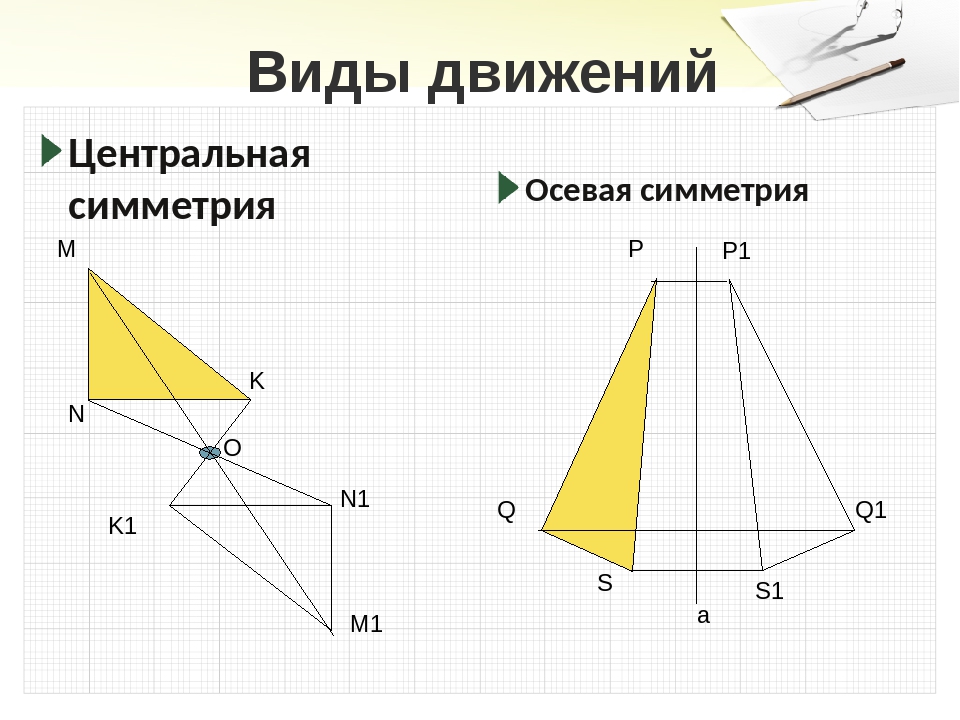
Я создатель, любящий выкройки. Я никогда не был хорош в фигуративном искусстве, но дай мне расслабиться с геометрическими фигурами, и я не могу перестать рисовать! Для сегодняшнего проекта я создал шаблон с простым трафаретом, который вы можете вырезать и использовать для украшения бумажной плитки, так же, как декоративные плитки, которые вы видите в испанской и исламской архитектуре.Я рекомендую вам распечатать это на картоне, если возможно, это сделает трафарет более прочным, но бумага работает в крайнем случае.
Материалы для бумажных плиток
Этот проект был создан для инициативы HP Print & Learn летом 2020 года. Вы будете перенаправлены на веб-сайт HP для загрузки шаблона.
Советы
- Этот шаблон лучше всего подходит для печати на карточках.
- Каждая пунктирная линия на плитке представляет собой ось.
- Создайте свой узор так, чтобы формы были симметричными по обе стороны от каждой оси.
- Формы перекрытия для создания сложных дизайнов и узоров.
Let’s Talk STEAM
Art Геометрическое искусство — это вид искусства, в котором для создания композиций используются геометрические формы и линии. В 20 веке это называлось геометрической абстракцией. Художники, известные своим геометрическим искусством, часто накладывают друг на друга формы, линии и цвет, создавая современное, минималистичное, а иногда и игривое искусство.Здесь вы можете увидеть некоторые примеры геометрического искусства и узнать больше об отдельных направлениях искусства, в которых оно использовалось.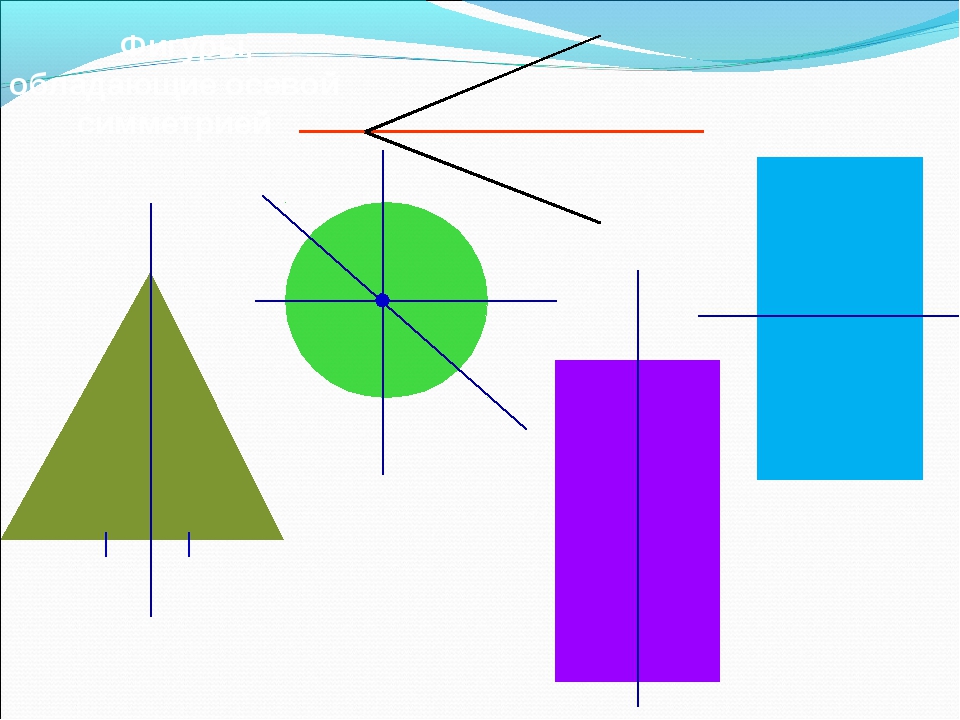
Декоративная плитка является основным элементом исламской и испанской архитектуры. В исламском искусстве фигуративные изображения не используются, поэтому художники используют сложные, накладывающиеся друг на друга геометрические узоры на плитках и других объектах, используемых в архитектуре и дизайне. На персидских и турецких коврах используется замысловатый узор. Вы можете узнать больше об исламском геометрическом узоре и увидеть примеры здесь и здесь.
Испания находилась под властью ислама в Северной Африке в течение 800 лет, и декоративные традиции использования узорчатой плитки преобладают и в ее архитектуре. Испанский геометрический дизайн плитки обычно менее сложен, чем декоративная плитка исламского искусства. Вы можете увидеть несколько примеров здесь.
Math Ось представляет собой прямую линию, вокруг которой вращаются геометрические фигуры. Каждая пунктирная линия на шаблоне плитки представляет собой ось. Оси, которые проходят по горизонтали и вертикали, имеют ортогональность . Оси, идущие от угла к углу, имеют диагональ .
Оси, которые проходят по горизонтали и вертикали, имеют ортогональность . Оси, идущие от угла к углу, имеют диагональ .
Симметрия — это согласование положения объекта или узора по обе стороны от оси. Создайте свой узор так, чтобы формы были симметричными по обе стороны от каждой оси.
ПодробнееЕсли вам понравился этот проект геометрического искусства, вот еще два, которые вы можете попробовать: Infinity Tiles и String Art Stars
Детский урок рисования фруктов геометрической симметрии —
Фрукты с геометрической симметрией для детей
Урок рисования
Автор Спрамани Элаун
В этом блоге я хочу дать вам несколько простых уроков рисования геометрических фигур и симметричного баланса.
Я также прилагаю список рекомендуемых материалов.
Практически все, что мы рисуем, начинается с определения общей формы или формы.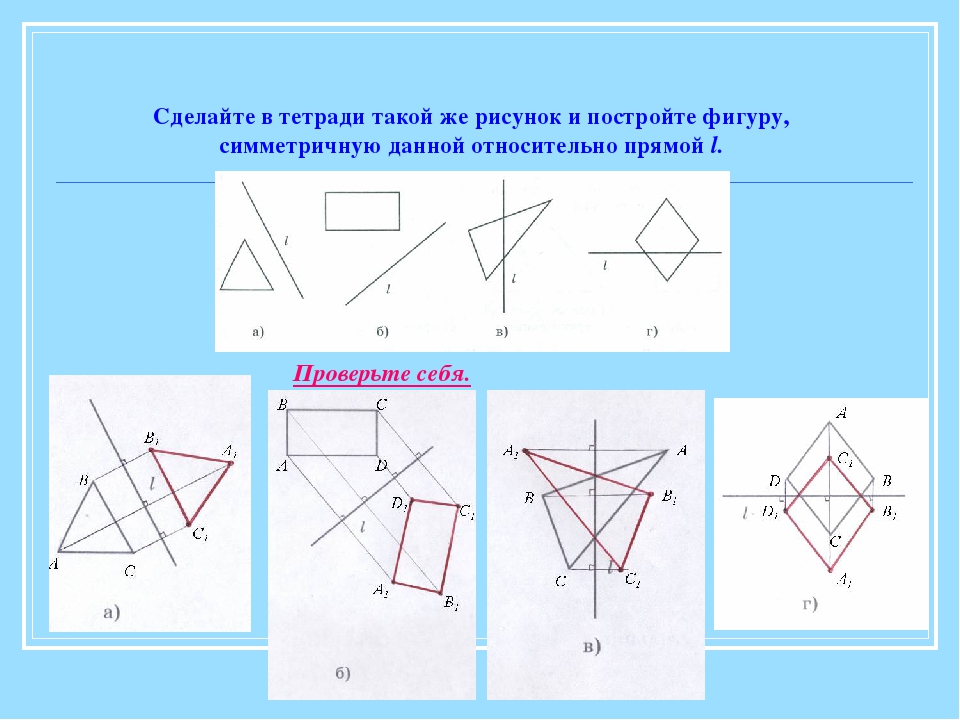
Геометрия и симметрия очаровали многих из нас, включая великих умов, таких как философы, астрономы, математики, художники, архитекторы и физики.
Геометрические формы и симметрия могут быть интересными для детей, когда они связаны с миром природы.
Узоры симметрии можно заметить во многих природных объектах, даже во фруктах!
И младшие, и старшие классы действительно любят рисовать фрукты, когда они открывают для себя удивительные природные узоры внутри них.
Простой запуск
Этот урок можно пройти за один день или разбить на более мелкие уроки.
Если дети сначала учатся рисовать основные геометрические фигуры, это может помочь им перед тем, как пытаться рисовать фрукты.
Для маленьких детей 1–4 классов я рекомендую просто потренироваться в рисовании плоских двухмерных геометрических фигур.
Детям младшего возраста нужно больше времени, чтобы научиться рисовать линии пропорционально.
Учащимся старшего возраста можно предложить создать геометрические узоры с большей детализацией и последовательными пропорциями.
Учащиеся старшего возраста также могут научиться создавать объем и пространство, рисуя трехмерные линии.
Урок 1. Рисунки геометрических фигур
Вам понадобятся художественные принадлежности:Бумага для эскизов от 3 до 5 листов или журнал для рисования
Графитный карандаш
Ластик
Линейка
Таблица геометрических форм
Картины или натюрморты фрукты, нарезанные дольками
Покажите детям геометрические фигуры и их внешний вид.
Если хотите, можете пройтись по названиям этих фигур и выделить простые формы вокруг них.
Попросите учащихся нарисовать пару фигур без штриховки, просто по одной линии.
Возможно, вам потребуется продемонстрировать, как рисовать прямые линии с помощью линейки и как рисовать изогнутые круглые формы.
Студентам, возможно, потребуется научиться стирать линии, пока они не получат нужную форму.
На этом шаге может потребоваться несколько рисунков, пока дети не будут довольны своими формами.
Позвольте детям попрактиковаться в этом, пока они не научатся рисовать узнаваемые формы.
Для детей постарше вы можете обсудить, как геометрические фигуры могут выглядеть трехмерно, создавая объем или пространство с помощью линий.
Покажите детям, что такое симметрия и как выглядит симметричный баланс.
Покажите примеры осевой линии симметричной формы и того, что обе стороны всегда равны.
Попросите детей вылепить от двух до трех геометрических фигур, а затем нарисовать центральную линию, чтобы показать симметричный баланс с обеих сторон.
Пусть дети начертят геометрические фигуры в симметричный сбалансированный узор.
Это может быть очень просто для маленьких детей и сложнее для старших.
Покажите детям примеры простых и сложных рисунков.
Попросите детей посмотреть натюрморт или картинки с разрезанными фруктами, открывающими узоры внутри.
Попросите их увидеть, есть ли какие-нибудь геометрические фигуры или узоры.
Попросите детей нарисовать любую геометрическую форму или узоры, которые они узнают.
Спросите детей, есть ли баланс симметрии в этих узорах, которые они видят.
Урок 2. Цветная иллюстрация фруктов
Товары для творчества вам понадобятся:
Бумага для рисования — 8 1/2 x 11
Графитный карандаш
Ластик
Линейка
Color Medium — Цветные карандаши
Картины или натюрморт, разрезанные на кусочки фрукты
Попросите учащихся выбрать фрукт геометрической формы, узор с симметричным балансом.
Нарисуйте фрукты графитным карандашом и сотрите все ненужные линии и отметки, когда будете довольны фруктами.
Попросите учащихся раскрасить фрукты.
Убедитесь, что дети также раскрашивают фон, чтобы завершить иллюстрацию.
Для старшеклассников в качестве дополнительного шага используйте такие материалы, как гуашь, сухие акварельные лепешки или микс.
В этом блоге я показал вам несколько уроков, которые развивают навыки рисования, наблюдая геометрические формы и симметрию в натуральных фруктах.
С помощью простых упражнений по рисованию дети могут распознать симметричные узоры на фруктах.
Я также поделился своим базовым списком предметов искусства для выполнения этих уроков.
И самое главное, что я поделился, это то, что все возрасты любят этот проект.
Вы можете настроить упражнения по рисованию так, чтобы они были проще для детей младшего возраста и сложными и интересными для старших классов.
Объем и последовательность занятийОпределение геометрических форм, определение геометрических форм в природе, основы практики рисования, использование линейки для построения прямых линий, обучение созданию кривых округлых форм, обучение рисованию и стиранию, определение симметрии, определение симметрии в природных объектах, обучение балансированию форм в симметричные узоры, определение симметричной центральной точки, композиция и зарисовка фруктов и отработка цветного карандаша.
Почему трудно преподавать детям уроки рисования | начальные классы
Обучай рисовать и рисовать, не зная, как
Все права защищены © Nature of Art For Kids®
Никакая часть этого блога не может быть использована или воспроизведена каким-либо образом без письменного разрешения, за исключением кратких цитат, содержащихся в критических статьях и обзорах.
линий симметрии | Помощь с математикой
Выводы: После этого урока учащиеся смогут:
- Определить, является ли фигура симметричной
- Нарисуйте линии симметрии на фигуре
- Завершить рисунок по линии симметрии
Этот раздел поможет вашему ребенку определить, симметрична ли фигура.
Фигура считается симметричной, если ее можно разделить точно пополам. Посмотрите на пример ниже.
| Симметрия означает, что обе стороны являются одинаковыми при разделении пополам. |
Обратите внимание, что обе стороны счастливого лица выглядят совершенно одинаково. Это означает, что эта фигура симметрична.
Посмотрите на следующий пример. Эта фигура симметрична? Он выглядит одинаково по обе стороны от линии?
| У этого восьмиугольника более одной линии симметрии.Сможешь найти остальных? |
Восьмиугольник симметричный. Если вы сложите его там, где находится линия, каждая сторона будет идеально соответствовать. Но как узнать, что фигура НЕ симметрична? Посмотрите на пример ниже. Эта фигура не симметрична. Вы можете понять почему?
| Обе стороны не одинаковые! |
Молния не является симметричной, потому что она не разделяется пополам с двумя равными сторонами.Один простой способ узнать, симметрична ли фигура, — это нарисовать ее на бумаге и сложить пополам. Если стороны полностью совпадают, это симметрично.
Рисование линий симметрииЭтот раздел поможет вашему ребенку рисовать линии симметрии на фигуре.
Линия симметрии делит фигуру пополам. Фигуры могут иметь более одной линии симметрии.
Посмотрите на квадрат ниже. Сколько линий симметрии вы считаете? Будьте осторожны, считайте каждую строку только один раз!
Имеет ли прямоугольник столько же линий симметрии, сколько квадрат? Помните, что линия симметрии разделит фигуру пополам, так что каждая часть будет абсолютно одинаковой.Обратите внимание, что у прямоугольника на две линии симметрии меньше. Вы можете подумать, в каком направлении не может идти линия симметрии?
Прямоугольник не может иметь диагональную линию симметрии, как квадрат, потому что стороны не одинаковой длины. Если вы сложите этот прямоугольник по диагонали так, чтобы угол A пересекался с углом D, стороны не совпали бы , а не . Попробуйте это с блокнотом!
Вы можете рисовать линии симметрии на самых разных фигурах. Посмотрите на линии симметрии на рисунках ниже.Обратите внимание, как разные типы фигур могут иметь разное количество линий симметрии.
Создание симметричных фигурЭтот раздел поможет вашему ребенку нарисовать линию симметрии.
Посмотрите на рисунок ниже. Рисуется только половина. Вы можете использовать линию симметрии в качестве ориентира, чтобы нарисовать вторую половину. Начните с точки на линии симметрии и нарисуйте то же самое на другой стороне.
| Проведите горизонтальную линию Проведите вертикальную линию Проведите горизонтальную линию Проведите диагональную линию |
Рисунок A — это исходный чертеж, а рисунок B — симметричная или идентичная деталь.
ПримерыНа приведенном ниже рисунке показано количество линий симметрии различных типов фигур. Обратите внимание, что для правильных многоугольников количество линий симметрии такое же, как и количество сторон фигуры.
Таблицы симметрииВы можете щелкнуть приведенные ниже ссылки и попросить ребенка попробовать рабочие листы симметрии. Эти рабочие листы помогут практиковать то, что показано выше.
Симметрия в вашей жизни (деятельности)Вот список действий, которыми вы можете заниматься дома или в вашем районе, чтобы помочь понять симметрию.
- Симметрия в супермаркете
- Пойдите в супермаркет и найдите симметричные коробки, контейнеры и упаковки.
- Посмотрите на разные фрукты и овощи. Какие симметричны, а какие нет? Что может быть симметричным — фрукты или овощи?
- Симметрия в природе
- Осмотреть цветы, деревья, листья на симметрию
- Сфотографируйте насекомое — где линия симметрии?
- Симметрия в вашей спальне
- Определите линии симметрии на вашей кровати, телевизоре, игровой системе, компьютере и дверце шкафа.
- У кого в спальне более симметричные фигуры — у тебя или у твоего брата или сестры? Сколько еще симметричных фигур вы видите?
- Симметрия кухни
- Используйте коробки или контейнеры из кухонных шкафов, чтобы создать симметричную фигуру по обе стороны от линии симметрии (вы можете использовать метр или длинный кусок ленты в качестве линии симметрии).
- Район охоты за мусором
- Ищите примеры симметрии, просто прогуливаясь по окрестностям.
- Запишите рисунки или изображения симметричных фигур.
Советы по рисованию симметрии | Sciencing
Симметричный рисунок имеет идентичные части, отражающие друг друга по линии симметрии. Эту симметрию можно найти во всей природе, включая человеческое тело, форму листьев и крыльев бабочки. Создание искусства, демонстрирующего симметрию, может быть трудным, поскольку две половинки на линии симметрии должны быть идентичны.Художник использует практику и несколько полезных руководств, чтобы рисовать симметричные изображения.
Зеркальное отображение
Вы можете практиковать симметрию в рисовании, практикуясь с зеркалом. Проведите прямую линию с помощью линейки на вертикальной или горизонтальной оси. С одной стороны от прямой нарисуйте половину фигуры. Например, нарисуйте половину креста или сердечка. Используйте линейку, чтобы определить размеры нарисованной вами половинки. Используйте эти измерения, чтобы создать зеркальное отображение полуформы на другой стороне линии симметрии.Практикуйтесь в использовании различных форм, например, с прямыми линиями и углами, а также с изогнутыми линиями. Чем больше у вас будет практики с основными формами, тем лучше вы будете позже создавать более подробные симметричные изображения.
Линии сетки
Сетки — еще один способ создания симметричных изображений. Нарисуйте сетку, используя отметки светлым карандашом и линейку. Важно, чтобы все линии сетки были прямыми, а прямоугольники были одного размера. Если коробки неправильные, рисунок тоже будет.Определите, какая линия на сетке является центром или линией симметрии сетки. Нарисуйте половину изображения, которое вы хотели сделать. Используйте сетки как способ измерения расстояния от линии симметрии и размера объектов. Когда рисунок будет завершен, сотрите все линии сетки.
Произвольный набросок
Произвольный набросок также можно использовать для тренировки симметрии. Используйте изображение объекта в качестве ориентира и от руки нарисуйте основной контур объекта. Используйте легкие карандашные отметки, чтобы создать набросок от руки, потому что большая часть этих отметок будет стерта или изменена позже.Определите, где находится линия симметрии на объекте, и с помощью линейки проведите эту линию. Используйте эскиз как ориентир, чтобы добавить более подробные изображения на одну сторону линии симметрии. Создайте зеркальное отображение детализированного изображения на другой стороне линии симметрии.
Лица
Лица сложно рисовать, и они редко бывают идеально симметричными. Однако вы можете попрактиковаться в рисовании симметричных лиц с помощью фотографий. Сделайте изображение лица и проведите вертикальную линию через центр носа, чтобы создать линию симметрии.Вырежьте изображение по этой линии. Прикрепите к изображению белый лист бумаги, чтобы нарисовать другую сторону лица. Вначале может быть полезно использовать технику сетки, чтобы запечатлеть все черты лица. По мере улучшения снимите сетку и нарисуйте зеркальное отображение лица.
Математика: раскраски с симметричным узором
Этот пост может содержать партнерские ссылки.
Если вы ищете увлекательный способ объединить математику и искусство, эти раскраски с симметричным узором — отличный способ начать!
Карты для раскраски и соответствия симметричным узорам
Эта неделя посвящена математике на моем сайте, поскольку мы приближаемся к неделе, когда выходит моя книга «Искусство математики и игры для детей»! На этой неделе у меня проходит серия под названием «Удивительные математические художественные проекты для детей», обязательно посмотрите ее и следите за ней всю неделю!
Раскраски с симметричными узорами
Этот набор для печати по математике состоит из 2 частей.Существует набор карточек для раскраски с половиной изображения, которые дети могут подобрать и раскрасить. Есть десять различных узоров, которые можно раскрасить. Я включаю их как в цвете, так и в черно-белом. Они помогают детям узнать о симметрии, помогая им создать идентичный узор на пустой стороне.
Во второй части этого набора выкройки завершены, но есть линия, где вы можете разрезать их пополам, чтобы составить из них совпадающие пазлы. Они отлично подходят для детей, которые, возможно, немного моложе или плохо знакомы с симметрией.
Зачем учить симметрии?
Симметрия — это часть геометрии. Когда дети узнают о геометрических формах, им нужно будет понять симметрию. Также существует симметрия во всех частях окружающего нас мира. Мы можем не часто узнавать его, поскольку он нам так знаком. Изучение и понимание симметрии помогает детям на уроках математики найти связь с реальной жизнью. Существует так много способов использования симметрии в жизни и в различных сферах деятельности! Математики, художники, дизайнеры, инженеры и даже музыканты и танцоры!
Мои дети были в восторге от этого! Моей младшей 5 лет, и ей было немного сложнее.Она намного лучше справлялась с головоломками. Это был идеальный уровень для нее. Они идеально подошли моему 8-летнему сыну, который учится в 3-м классе.
Как распечатать раскраски с симметричным узором
Вы можете найти их в моем магазине здесь:
4,00 $ В корзину
См. Другие проекты математического искусства в моей книге «Искусство математики и игры для детей».
Также посмотрите мои симметричные рисунки снежинок!
Как сделать круговую географическую доску Удивительные проекты математического искусства для детейНужны творческие идеи обучения?
Подпишитесь на мои еженедельные обновления по электронной почте и получите доступ к моей БЕСПЛАТНОЙ библиотеке печатных форм.
Смотрите мою политику конфиденциальности.Симметрия: определение, типы, упражнения и примеры
Сегодня вы узнаете, что такое симметрия, и мы увидим некоторые упражнения на симметрию, которые дети делают во время своих занятий Smartick, и типичные ошибки, которые обычно допускаются.
Что такое симметрия?
Симметрия — это одно из математических понятий, которое учащиеся начинают изучать вне школы. Тем не менее, они все еще изучают его в дошкольном образовании и строят симметричные фигуры, не прибегая к строгому определению.
Как мы увидим ниже, существуют различные типы симметрии. Мы начнем с наиболее известной симметрии относительно прямой или осевой симметрии . Давайте начнем с рисования прямой линии на плоскости, в данном случае это может быть лист бумаги с сеткой, как показано на рисунке ниже:
Линия нарисована вертикально, но может быть горизонтальной или иметь любое другое направление.Мы говорим, что фигура симметрична относительно линии, когда каждая точка на одной стороне этой линии имеет другую точку на другой стороне и на том же расстоянии от этой линии.
Если мы хотим знать, симметрично ли изображение относительно линии и есть ли оно на листе бумаги, нам просто нужно сложить бумагу по линии. Если, когда мы складываем бумагу, фигуры совпадают друг с другом, это потому, что они симметричны относительно линии. Если они не совпадают, значит, они не симметричны.
Если мы хотим создать симметричное изображение на бумаге, мы начинаем с того, что складываем бумагу и, используя маркер, который будет слегка растекаться по бумаге, рисуем желаемую фигуру.Затем разворачиваем бумагу. Маркер просочился на другую сторону и создал две фигуры, симметричные относительно линии, которую мы сложили. Когда бумага сложена, они точно совпадают. Вместо маркера можно было бы использовать ножницы.
Видео: симметричные фигуры и оси симметрии
Чтобы лучше понять, что такое симметрия с относительно оси , взгляните на это видео одного из наших интерактивных руководств. Он больше не интерактивен, но у вас есть то преимущество, что вы можете смотреть его столько раз, сколько необходимо, и делиться им с другими.Если вы хотите получить доступ к настоящим интерактивным обучающим материалам, зарегистрируйтесь в Smartick, онлайн-методе обучения математике для детей от 4 до 14 лет.
В этом видео мы представляем семинар по симметрии, посмотрите:
Что такое ось симметрии?
Симметричная фигура может иметь одну или несколько осей симметрии, которые могут быть прямыми линиями или линиями, разделяющими фигуру на две симметричные части.
На изображении, взятом из видео, звезда имеет четыре оси симметрии, а руки имеют только одну — вертикальную прямую.
Типы симметрии
Существует много типов симметрии, но мы собираемся сосредоточиться на этих трех, которые можно увидеть в школе:
- Во-первых, осевая симметрия или симметрия относительно линии, — это та, которая делит объект или фигуру пополам, используя прямую линию , другими словами, осью симметрии. Этот тип симметрии может напоминать, когда мы смотрим в зеркало и видим в нем свое отражение.
- Мы говорим, что одна или несколько фигур имеют симметрию вращения , когда они не изменяются при повороте на определенный угол.Четырехконечная звезда на предыдущем изображении имеет симметрию вращения, потому что если вы повернете ее на 90 ° (или любое кратное 90 °), оно будет таким же.
- Третий тип симметрии на плоскости — это симметрия относительно точки или центральная симметрия . Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия дает тот же эффект, что и поворот на 180 °.
Упражнения по симметрии в Smartick
В посте о новом контенте Smartick мы привели примеры последовательности действий симметрии. Сложность зависит от формы фигур и ориентации оси симметрии. Сложность постепенно увеличивается, облегчая изучение и понимание этой концепции. Эти упражнения способствуют развитию пространственного видения и геометрического мышления.
- У нас есть упражнения, в которых дети должны проанализировать, симметричны ли две фигуры:
- В других они должны построить симметричные фигуры:
- Или поместите ряд точек симметрично на наклонной оси:
Типичные ошибки
Эти две фигуры симметричны относительно оси? Столкнувшись с этим вопросом, студенты часто допускают две ошибки.
- Подумайте, идентичны ли фигуры, если они симметричны:
Чтобы исправить эту ошибку (как мы упоминали ранее), полезно думать о сетке как о бумаге, которую можно складывать по оси симметрии. Если в сложенном виде фигуры не совпадают, то это потому, что они не симметричны.Другой способ — представить ось как зеркало. Если одна фигура не является отражением фигуры, которая проецировалась бы в зеркало, тогда они не симметричны.
- Другая распространенная ошибка — думать, что если одна фигура является зеркальным отражением другой, то они симметричны независимо от их положения относительно оси симметрии:
Мы можем использовать те же стратегии, что и раньше, чтобы исправить эту ошибку. Если сложить бумагу по оси симметрии, фигуры не совпадают.И одна фигура не является отражением другой в осевом зеркале. Следовательно, эти две фигуры не симметричны относительно оси.
Симметрия вне математики
Симметрия нас окружает:
- В зеркале или отражении на поверхности воды. Отраженное изображение симметрично реальному изображению.
- В нас самих: у нас есть правая рука и левая рука, правое ухо и левое ухо, и каждая пара симметрична. Наше тело разделено на две симметричные части, правую и левую, по отношению к оси, идущей от макушки до пальцев ног.
- Большинство домов и построек имеют фасады, симметричные относительно вертикальной оси.
- Машины, тостеры, сотовые телефоны, стакан, тарелка, бутылка, телевизор, диван… большинство повседневных предметов имеют одну или несколько осей симметрии.
- В искусстве можно найти симметрию. Художники используют симметрию в живописи, скульптуре, музыке и множестве других дисциплин.
- В природе тоже. Большинство животных и растений обладают той или иной симметрией: двусторонней, радиальной…
Если вы хотите узнать больше о геометрии и математике в начальной школе, зарегистрируйтесь в Smartick и попробуйте бесплатно.
Подробнее:
степень бакалавра коммуникативных расстройств и степень бакалавра испанского языка Университета Род-Айленда.
Степень магистра международного образования Университета Алькала — Института Франклина.
Она работала учителем в трех разных странах, а теперь работает переводчиком в группе создания контента в Smartick и помогает адаптировать контент для сообщений в блогах.
Как коренная жительница Род-Айленда, она любит любое занятие на воде, и когда она не работает, вы можете найти ее в путешествиях, кикбоксинге или пробовать новый рецепт.
Симметрия в искусстве с использованием Autodesk SketchBook
Об авторе
Мари-Ли — исследователь мира изобразительного искусства и начинающий дизайнер / художник. Она любит путешествовать по миру и узнавать обо всех культурах и историях каждого места. Мари-Ли — инуки, выросла в провинции Квебек, но сейчас живет в Икалуите, Нунавут.
Арт ДизайнРуководство
Введение
Вы когда-нибудь смотрели на домашнее задание по математике и думали, что оно красивое? Возможно, вы так не думаете, но математики находят красоту не только в математических вычислениях, но и в геометрических объектах, обладающих симметрией.Симметрия — это слово из греческого языка, которое означает «иметь согласие в размерах и пропорциях». Симметрия встречается во многих областях, таких как природа, архитектура, музыка и математика. Объект может иметь много типов симметрии, но сегодня мы сосредоточимся на отражающей или зеркальной симметрии, чтобы помочь нам создать цифровое искусство, вдохновленное цветочными работами / бисером.
Словарь
- Прозрачность: , сколько света может пройти через изображение.
- Непрозрачность: В графическом дизайне это относится к прозрачности изображения.Чем больше непрозрачность изображения, тем меньше оно прозрачности.
- Эллипс: геометрическая форма, которая выглядит как овал или сплюснутый круг.
- Motif: декоративный рисунок или узор.
- Ось, множественное число осей: воображаемая линия, фиксируемая с целью измерения координат. В двухмерных плоскостях есть горизонтальная ось X и вертикальная ось Y
- Симметрия: Двухмерный объект является симметричным, если вы можете провести через него линию, и обе стороны линии выглядят одинаково.В математике это объект, который не изменяется, когда он претерпевает преобразования, такие как отражение, вращение, перемещение и масштабирование.
- Вращательная / радиальная симметрия: Объект или изображение обладают вращательной симметрией, когда они выглядят одинаково после некоторого вращения вокруг центральной оси.
Эти снежинки радиально симметричны по 6 осям
- Двусторонняя симметрия: На этих изображениях показаны примеры двусторонней симметрии, поскольку обе половины изображения по обе стороны от оси идентичны.
Симметрия в природе
Эта морская звезда имеет радиальную симметрию
Этот тигр имеет двустороннюю симметрию рисунка меха
Симметрия в искусстве
Christi Belcourt, Water Song , (2010–11).Материалы
Загрузить Autodesk SketchBook
Компьютерная активность
- Откройте Autodesk Sketchbook и узнайте расположение ваших инструментов, посмотрев на панель инструментов в верхней части экрана.
- Выберите кисть, чтобы мы могли рисовать точками. В правой части нашей панели инструментов нажмите кнопку Brush Palette . Это откроет окно с различными вариантами кисти.
- Теперь мы установим размер и непрозрачность нашей кисти. Дважды щелкните кнопку шариковой ручки, чтобы открыть окно свойств кисти. Здесь вы найдете базовую вкладку и расширенную вкладку. На основной вкладке у нас есть два ползунка для регулировки размера и непрозрачности (темноты) наших мазков кисти.Установите ползунок размера на максимум (4,0) и непрозрачность на 100%
- Теперь мы установим интервал между нашими мазками. Щелкните вкладку «Дополнительно», и вы найдете разные раскрывающиеся меню. Щелкните Штамп, и появится ползунок Интервал. Установите значение 10. Это добавит промежуток между мазками кисти и создаст точечный вид.
- Нажмите кнопку редактора цвета на панели инструментов. Это откроет редактор цветов, который изменит цвет наших мазков.Выберите черный.
- Мы будем использовать некоторые вспомогательные инструменты, которые помогут нам создавать формы круга. Эти пунктирные круги помогут нам рисовать формы и сохранять их пропорциональными. На панели инструментов выберите инструмент эллипс. Сдвиньте его к середине страницы, нажав кнопку в центре, и перетащите его в середину страницы. Чтобы нарисовать круг, нажмите и удерживайте кнопку мыши и перетащите ее по направляющей круга.
- Теперь мы увеличим нашу направляющую круга, чтобы нарисовать больший круг снаружи.Нажмите левую кнопку и перетащите круг / кнопку, чтобы сделать круг побольше.
Повторите шаги 6 и 7, чтобы сделать еще два круга, так что всего у вас будет три круга. Должно получиться так:
- Закройте направляющую, нажав кнопку X внизу инструмента направляющей эллипса.
- Теперь мы можем приступить к рисованию цветочных узоров с помощью инструмента симметрии на нашей панели инструментов. Выберите кнопку симметрии.Это откроет разные варианты. Мы выберем Симметрию Y и Симметрию X. Это покажет пунктирную линию на осях x и y с кнопкой, где они пересекаются. Нажмите эту кнопку, чтобы перетащить наши линии симметрии к центру наших кругов.
- Теперь мы будем использовать чернильную ручку, чтобы нарисовать контур нашего дизайна. Выберите чернильное перо в параметрах кисти и дважды щелкните, чтобы открыть свойства. Измените размер на 3.0.
- Добавьте несколько длинных лепестков, щелкнув левой кнопкой мыши и перетащив мышь от центра нашего первого круга вверх, пока мы не дойдем до второго.
Нарисуйте ту же фигуру по горизонтали слева направо.
- Продолжайте добавлять формы в свой дизайн, например, эту форму сердца. Начиная с центрального круга, проведите прямую линию между двумя лепестками.
Добавьте вторую линию, чтобы сделать основу сердца.
Нарисуйте верхнюю часть сердца изогнутыми линиями
Отлично, давайте добавим немного листьев. Чтобы повернуть страницу, удерживайте клавишу пробела, нажмите и перетащите, чтобы переместить страницу.Мы нарисуем две слегка изогнутые линии от второго круга к третьему, чтобы получился наш первый лист.
На каждой стороне этого первого листа добавьте форму второго листа.
Вот наш готовый план!
- Теперь мы заполним формы в нашем дизайне, используя инструмент заливки заливкой. Нажмите кнопку корзины на панели инструментов и выберите нужный цвет с помощью редактора цветов.
Продолжайте и залейте остальную часть вашего дизайна цветом!
Если вы допустили ошибку, нажмите Ctrl-Z на клавиатуре, чтобы отменить действие, или вы можете использовать красную стрелку на панели инструментов.
Заключение
Мы хотим видеть то, что вы создаете! Сделайте фото или видео и поделитесь с нами своей работой по электронной почте [email protected] или отметив @pinnguaq в Facebook, Twitter или Instagram. Не забудьте добавить хэштег #LearnWithPinnguaq!
Ресурсы
Дизайн, вдохновленный Eruoma Awashish
Подробнее о традиционном искусстве
Посмотреть наш план урока «Создание традиционного метис-точечного искусства»
Ресурсы социальных сетей
Поделитесь своим мнением!
Не могли бы вы уделить время заполнению нашего опроса? Это позволит нам лучше понимать типы интересующего вас контента, чтобы в будущем мы могли создавать больше подобных ресурсов.



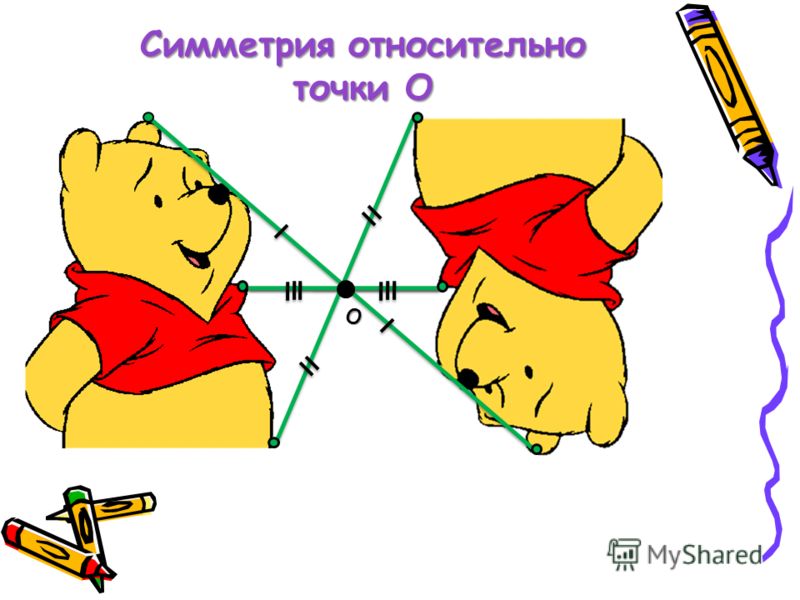
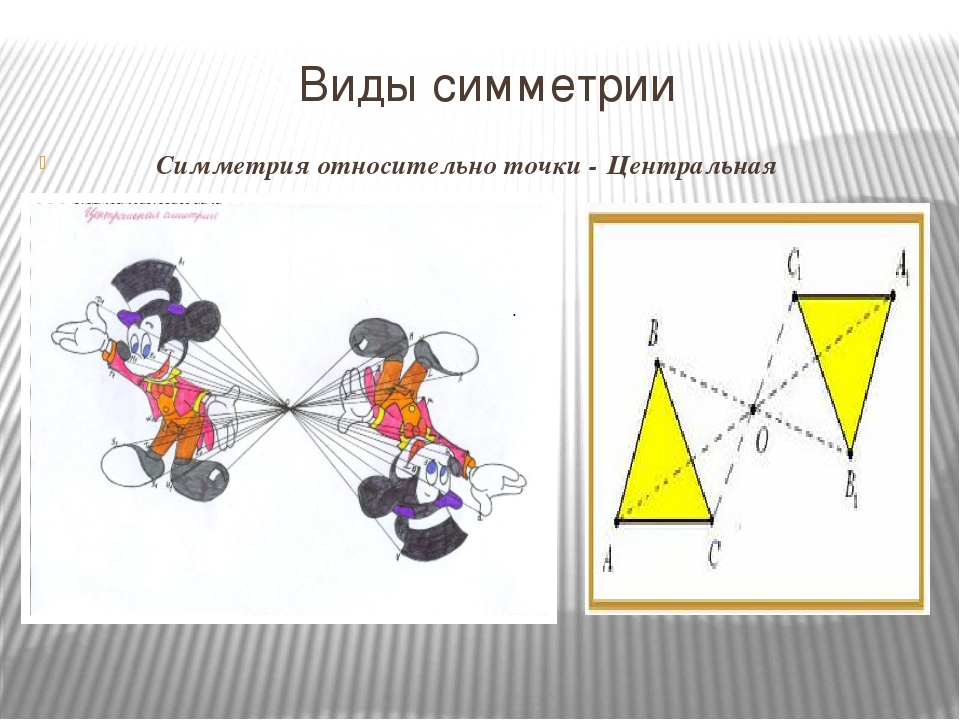
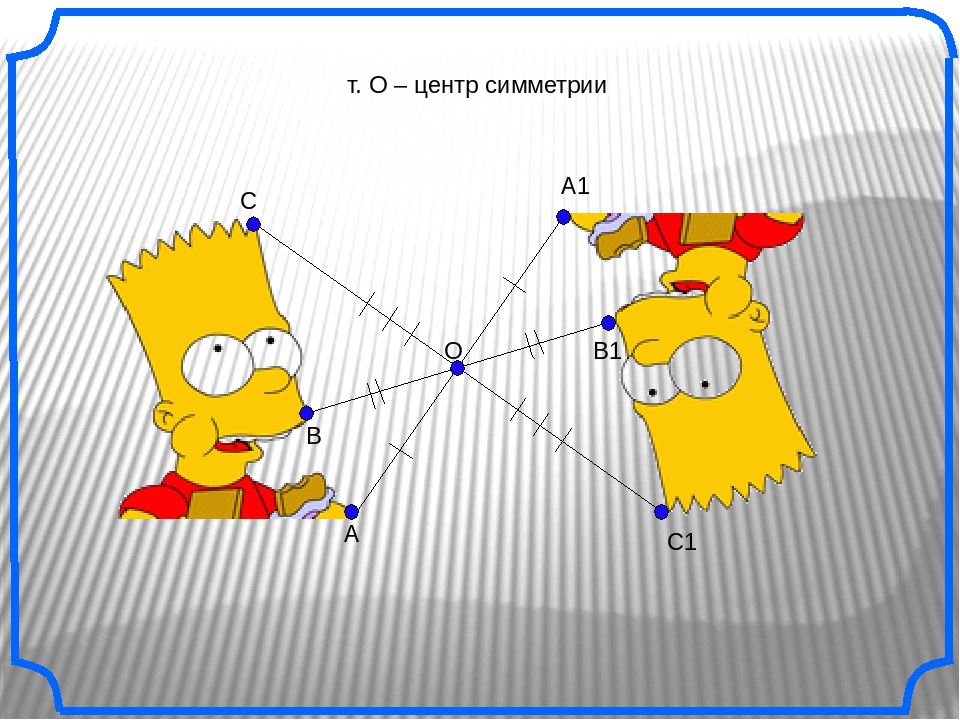
 )
) е. под углом в 90 0)
е. под углом в 90 0)
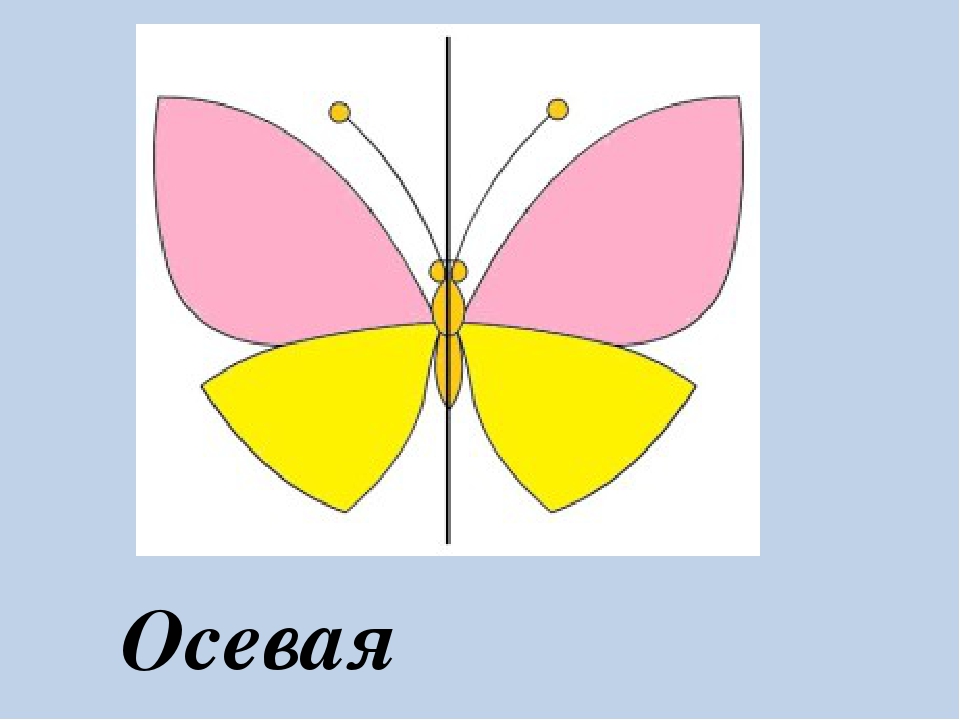
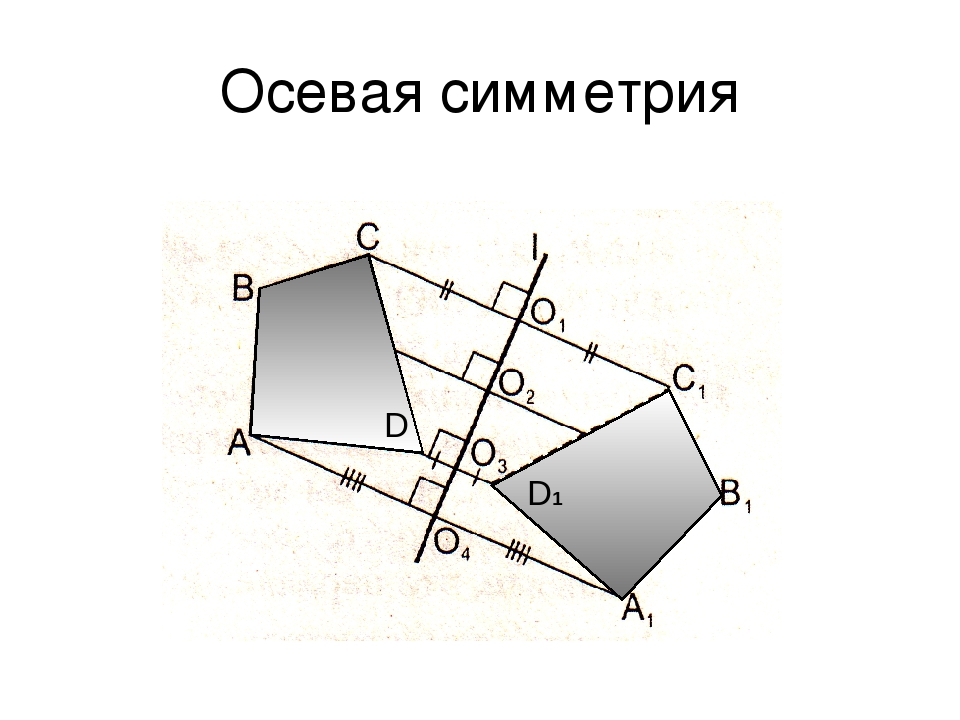 д.
д.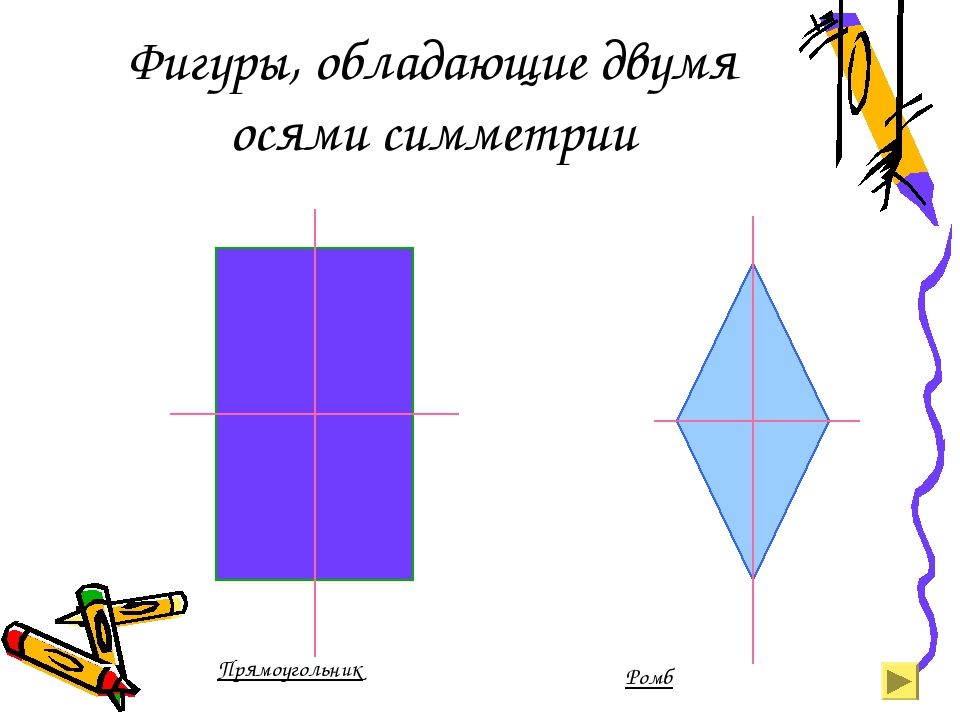 На примере изображения геометрических тел вращения усваиваются основные навыки академического рисунка. Для того, чтобы успешно рисовать сложные формы, сначала следует добиться грамотного выполнения простых заданий и хорошего уровня их выполнения. Любую форму, которую мы рисуем, при анализе можно представить как состоящую из простых геометрических форм, подход к изображению такой же, как при рисунке простых геометрических форм.
На примере изображения геометрических тел вращения усваиваются основные навыки академического рисунка. Для того, чтобы успешно рисовать сложные формы, сначала следует добиться грамотного выполнения простых заданий и хорошего уровня их выполнения. Любую форму, которую мы рисуем, при анализе можно представить как состоящую из простых геометрических форм, подход к изображению такой же, как при рисунке простых геометрических форм.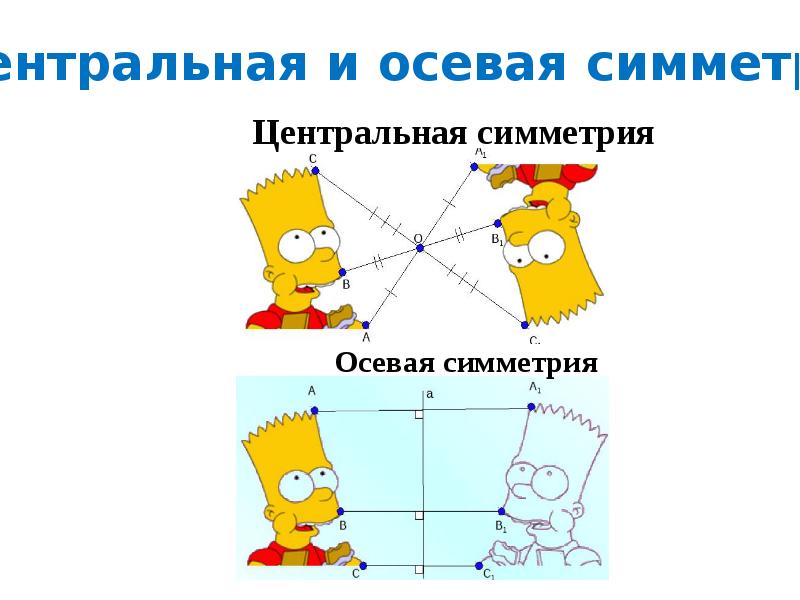 В нашем случае конус прямой, его ось перпендикулярна основанию.
В нашем случае конус прямой, его ось перпендикулярна основанию.
 На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.
На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию. Образующая представляет собой вертикальную линию, перпендикулярную основанию, которая вращается по окружности.
Образующая представляет собой вертикальную линию, перпендикулярную основанию, которая вращается по окружности.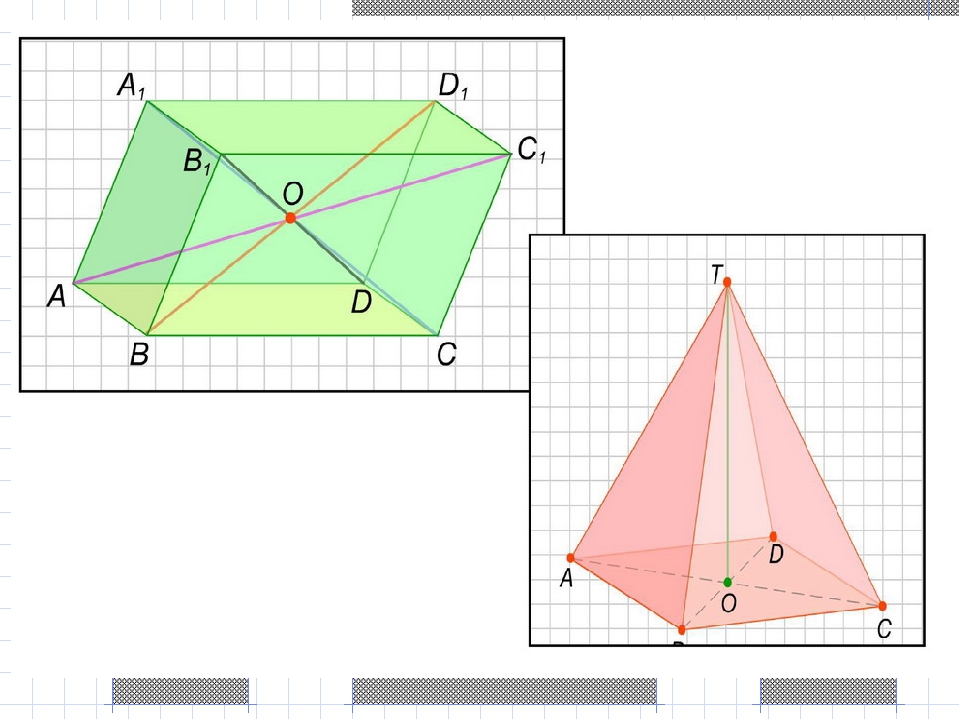
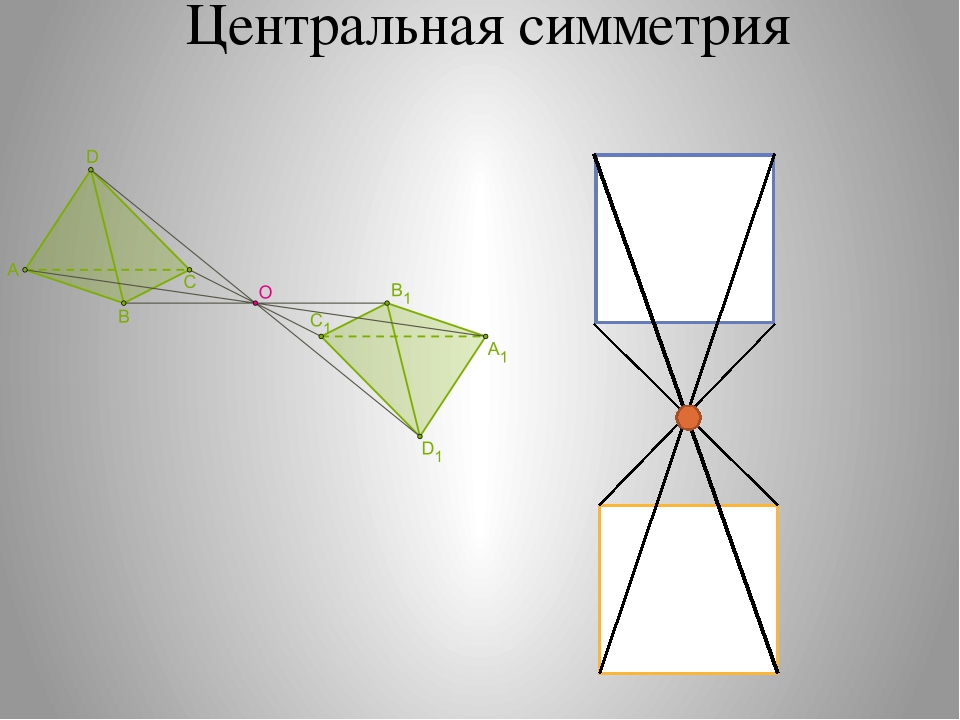 Верхняя часть чуть ближе к свету, она будет светлее. Теневая часть подсвечена снизу, а сверху тень в контрасте с верхним основанием. Поэтому самая тёмная часть тени окажется вверху.
Верхняя часть чуть ближе к свету, она будет светлее. Теневая часть подсвечена снизу, а сверху тень в контрасте с верхним основанием. Поэтому самая тёмная часть тени окажется вверху.