Японские задачи по математике в картинках: Математическая задачка родом из Японии для самых эрудированных
Сегодня мы предлагаем вам решить очередную головоломку. На этот раз она родом из Японии. Но это не судоку или какая-то сложная задача, с которой могут справиться лишь избранные. На самом деле это математическая задачка, которую должны решать ученики обычной школы.
Специалисты провели исследование, но его результаты их неприятно удивили. Оказалось, что 30 лет назад решение находили не менее 90% всех тестируемых. Но сегодня результаты намного хуже!
Правильный ответ дают лишь 60% молодых людей. Неприятная статистика навела исследователей на мысль, что современное образование уже не настолько эффективное, как было в прошлом.
Математическая задачка не для школьников: справитесь ли вы?
По сути, подобные примеры решают ученики средних, а иногда и младших классов. Но у многих взрослых почему-то возникают затруднения с правильным ответом. Хотя главное – понимать последовательность действий и алгоритм решения.
А это закладывают еще в школе. Если у вас не было проблем с математикой, то вы легко справитесь. Но не спешите – может быть, вы успели забыть, как решаются такие примеры.
На картинке мы даем вам уравнение, чтобы вы смогли вычислить правильный ответ. Каким, по вашему мнению, он будет? Многие решают уравнение по следующей схеме:
9 – 3 ÷ 1/3 + 1 = 9 — 3/1/3 + 1 = 9 — 3/3 + 1 = 9 – 1 + 1 = 9. — Но это неверный ответ!
На самом деле правильное решение – это 1. И вот почему: 9 – 3 ÷ 1/3 + 1 = 9 – 3 ÷ (1/3) + 1 = 9 – 3 × 3 + 1 = 9 – 9 + 1 = 1. Не так уж сложно, как кажется? Если вы попытались решить пример первым способом, значит, были невнимательны. Ответ элементарный, но требует сосредоточенности.
P.S. Поделитесь с нами в комментариях, смогли ли вы найти правильное решение? Искренне надеемся, что да! Конечно, школьники справляются с такими задачками за секунды, но взрослым может потребоваться больше времени. И это необязательно говорит о плохом уровне образования. Просто при отсутствии практики некоторые знания забываются, и вам становится непросто справляться с элементарными математическими действиями.
Источник
Вконтакте
Google+
Одноклассники
Кадр из фильма «Игры разума»
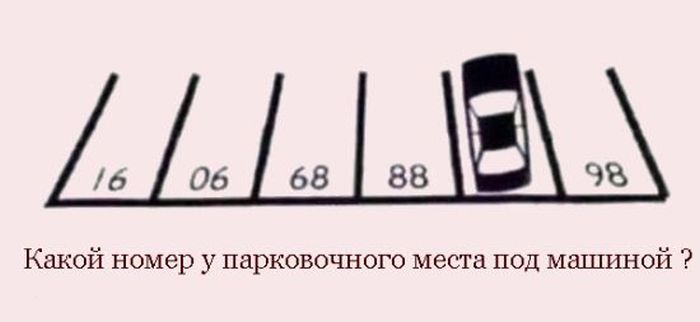
Номер парковочного места
Задачка для гонконгских школьников, которая набрала «вирусную» популярность в середине 2014 года. На её решение у шестилетнего ребёнка обычно уходит не больше 20 секунд, а вот неподготовленных взрослых она часто вводит в ступор.
Какое число скрыто под машиной?
Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.
Другая математика
Известная задача, которую дошкольники решают за 5-10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.

Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.
У этой задачи есть хороший аналог:
1 = 5
2 = 25
3 = 125
4 = 625
5 = ?
Ханна и резко повышенная сложность
Знаменитая задачка-мем, в которой итоговый вопрос кажется куда более сложным, чем условие.
В сумке n конфет. Шесть из них оранжевые. Остальные — жёлтые. Ханна берёт конфету из сумки и съедает. Затем берёт ещё одну и снова съедает. Вероятность того, что она съела две оранжевые конфеты — 1/3. Докажите, что n²–n–90=0.
Странное завершение истории Ханны породило в сети множество шуток. Самая известная: «Ханна съела несколько конфет. Рассчитайте длину окружности экватора Юпитера с помощью кальки и ржавой ложки».
Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить
Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.
Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.
Куда едет автобус
Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?

Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.
Для терпеливых
Ещё одна «вирусная» задачка. Как сообщает The Guardian, вьетнамский учитель даёт её восьмилетним детям, и они справляются. При этом решения за короткое время не смогли дать даже люди с докторской ст
1. Четырехзначные числа
Дошколята решают эту задачку за 5-10 минут. Программисты – за 1 час. Большинство людей с высшим образованием… Впрочем, проверьте на себе. И попытайтесь по-честному, не спешите узнать готовый ответ (он будет в конце, под всеми остальными заданиями).
Маленькая подсказка: попробуйте мыслить нестандартно.

Никак не сообразите? Для вас есть еще 2 подсказки (прочитайте сначала первую – если не поможет, то переходите ко второй).
1) Вспомните, кто быстрее всех решает эту задачу? Дошкольники. А почему? Думайте, как они.
2) Думайте «зрительно». Это не математическая задача.
2. Парковка
Еще один элементарный вопросец – на сей раз из гонконгского теста для зачисления в начальную школу. «Несмышленым» выпускникам детсада дается на решение 20 секунд!
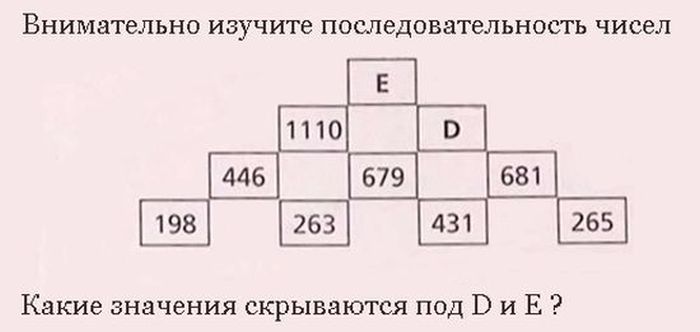
3. Числовая пирамида
И снова привет из Сингапура. Попробуйте сравняться в уме с местными третьеклассниками, которые запросто справляются с математической задачкой ниже. (Но если застрянете, не сильно огорчайтесь: как показал телевизионный опрос, взрослые сочли ее «трудной», «слишком заумной» и даже «неразрешимой»!)
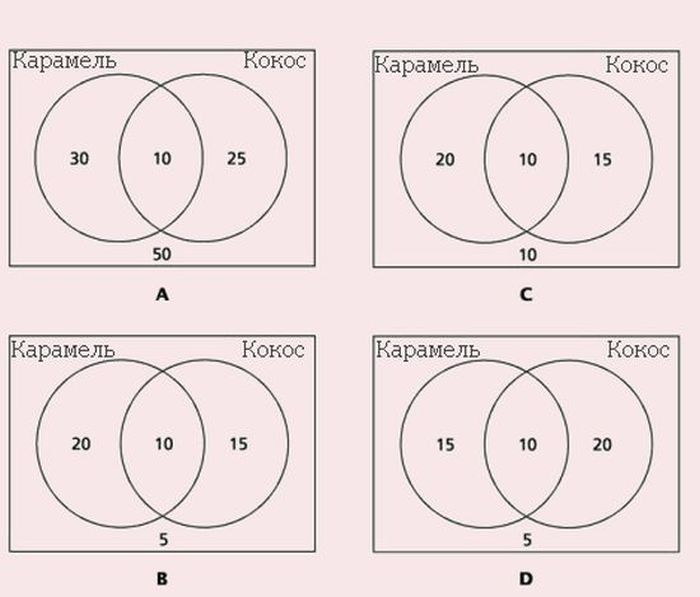
4. Шоколадная коробка
А теперь перенесемся в США. Вот вам одно из контрольных заданий обычных вашингтонских 7-классников (по местной системе это 12-13 лет).
«В коробке 50 шоколадок. Из них 30 с карамелью, 25 с кокосом, 10 – и с карамелью, и с кокосом, а остальные вообще без начинки.
Вопрос: Какая диаграмма верно отражает содержимое коробки?»
5. Родственные связи
Ну и напоследок загадка, которая даже не связана с математикой. Тем не менее она заводит в тупик многих взрослых, тогда как дети почти мгновенно выдают правильный ответ!
Вопрос: Как же такое возможно?»

Ответы и способы решений
1. Четырехзначные числа
Ответ: 2581 = 2
В каждой группе из 4 чисел нужно было всего лишь сосчитать замкнутые кружочки. Например, у цифры 6 один кружочек, у цифры 8 — два. А значит у числа 6889 их шесть. И так далее.
2. Парковка
Ответ: 87
Стоило просто мысленно повернуть картинку вверх ногами.
3. Числовая пирамида
Ответ: D = 1345; E = 2440
Первым делом складываете два числа в нижнем ряду: 198 + 263 = 461
Получилась сумма больше того числа, что стоит над ними: 461 > 446
Вычитаете из большего меньшее: 461 — 446 = 15
Точно так же считаем остальные пары и видим, что везде получается 15. Та-дам! Вот и ключ к решению.
4. Шоколадная коробка
Ответ: диаграмма B
Простая арифметика:
Сколько шоколадок только с карамелью? 30 — 10 = 20
Сколько шоколадок только с кокосом? 25 — 10 = 15
Сколько же остается шоколадок без начинки? 50 — (20 + 15 +10) = 5
5. Родственные связи
Ответ: хирург – это мать ребенка.
9 964

Задачи сложные, ответы на них – очень просты, но это когда после подсмотрите.
Предлагаем вам попробовать решить интересные 5 загадок на логику. По общей статистике участвующих людей в этом тесте угадывают верно всего лишь 20 процентов из 100%. Попробуйте и вы свои силы в этом забавном мероприятии тест-викторины, и быть может вам удастся причислить себя к победителям? Ну а если не получится, так все ровно будет интересно и полезно, так как верные ответы на каждую загадку вы все ровно узнаете, и конечно же запомните.
Задача № 1
Первая задача: посмотрите внимательно на картинку, и ответьте, сколько смартфонов возможно подключить и зарядить одновременно в этих розетках?

Ответ (нажмите ниже на строку № 1)
Ответ на задачу № 1
Из 6 удлинителей 1 без провода, еще 1 с оторванным проводом, а удлинитель с 1 розеткой бессмысленен. Остается три удлинителя с тринадцатью розетками. Из этих тринадцать одна розетка бракованная – только 1 отверстие под вилку; еще две розетки станут заняты для подключения удлинителей. Остается десять розеток. + на одном из удлинителей просто USB-разъем. Поэтому как итог, подключить можно одиннадцать зарядок.
Вторая задача: угадайте, сколько лиц на этой картинке?
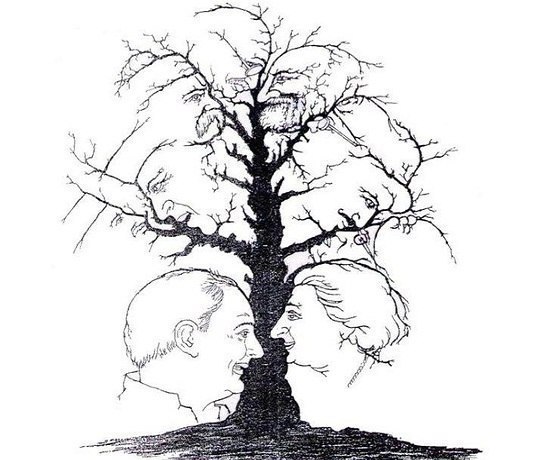
Ответ на задачу № 2 (нажмите ниже)
Ответ на задачу № 2
Ответ: Всего десять лиц – по пять с каждой стороны дерева
Задача № 3
Переставьте числа в квадратах таким образом, чтобы два следующих друг за другом не оказались в соседних клетках — не вертикально, не горизонтально и не диагонально.
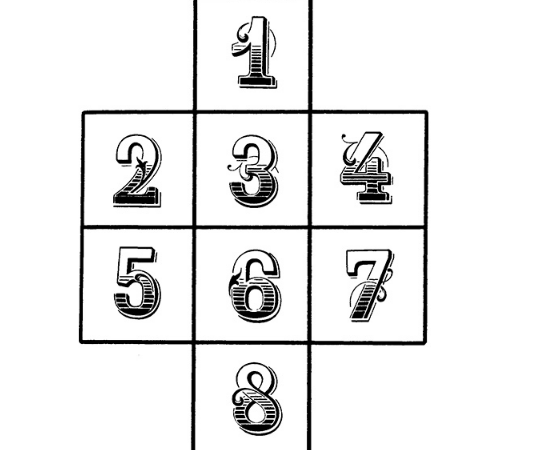
Ответ на задачу № 3 (нажмите ниже)
Ответ на задачу № 3
2 ______ 5 8 6 _______ 3 1 4 _______ 7
Задача на логику № 4
Найдите среди этих книг, где расположен 6 том?

Ответ на задачу № 4 (нажмите ниже)
Ответ на задачу № 4
Ответ: шестой том перевернули и поставили с левого края (который виден сейчас таким образом как том под номером 9)
Задача № 5 на логику, а главное на внимание

Посмотрите внимательно на эту картинку и найдите на ней ошибку. Где тут ошибка?
Ответ на задачу № 5 (нажмите ниже)
Ответ на задачу № 5
Ответ: Ошибка находится в слове “ошибка” что расположена в самой нижней строке, в правом нижнем углу.
Умнее ли вы японского школьника? :: Инфониак
 Тесты
Тесты Такие геометрические головоломки уже стали популярными в Японии.
Их придумал Наоки Инаба (Naoki Inaba), известный создатель логических головоломок, чьи работы публикуются в различных журналах.
Свою первую головоломку он придумал после просьбы директора школы создать логическую задачку.
Инаба называет работы Menseki meiro (можно перевести как «паутина площадей»). В них вам нужно найти площадь прямоугольника, его длину или ширину.
Правила:
-
Можно использовать только формулу вычисления площади прямоугольника, то есть S = a * b (a — длина, b — ширина). Нельзя использовать десятичные дроби. Нельзя использовать уравнения с неизвестными. Используйте только целые числа.
-
Можно дополнять рисунки.
Задачка 1 (для разогрева)
Ответ в конце теста.

Читайте также: Шпионский тест: Только человек с нестандартным мышлением сможет найти секретное слово
Задача 2

Задача 3

Ответы:
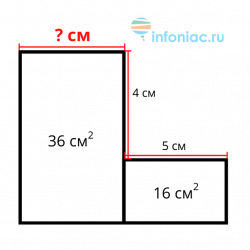
Задача 1.
Ответ: 5 см.
Дорисовываем синий прямоугольник. Стороны у него 4 и 5, а значит площадь 20. Соединяем с площадью маленького прямоугольника и получаем 36 [20 + 16]. Такая же площадь большого прямоугольника.
Поскольку они имеют одинаковую высоту, они должны иметь одинаковую ширину, а значит ширина большого прямоугольника равна 5 см.
Задача 2
Ответ: 20 кв. см.
Длина отрезка X равна: (38 + 39) / 7 = 77/7 = 11 см
Длина отрезка Y равна: 11 — 4 = 7 см
Длинна отрезка Z равна: 7 + 3 = 10 см
Следовательно, недостающее значение (10 x 6) — 40 см2 = 20 см2
Второй вариант решения:
Дорисовываем синие вспомогательные прямоугольники. Нам нужно узнать площадь всего большого прямоугольника, в который входят все фигуры. Для этого нам нужно узнать его длину и ширину.
1. Узнаём длину:
1.1. Общая площадь верхних двух прямоугольников равна: 38 + 39 =77. Если ширина 7, значит длина этого общего прямоугольника 77:7=11.
1.2. Длинна маленького верхнего отрезка 3, а значит длина всего большого прямоугольника 11 + 3 = 14
2. Узнаём ширину:
Часть ширины равна 7, а другая часть равна 6, значит ширина всего большого прямоугольника равна 13.
3. Площадь большого прямоугольника: 14 х 13 = 182.
4. Площадь нижнего синего прямоугольника: 6 х 4 = 24
5. Площадь верхнего синего прямоугольника: 3 х 7 =21.
6. Отнимаем от всей площади, те площади, которые знаем, и получаем площадь серого прямоугольника: 182 – 77 – 40 – 21 – 24 = 20.
Задача 3
Ответ: 10 см.
1. Сначала мы можем сделать вывод, что длина синего прямоугольника равна 5 см, поскольку 4 x 5 = 20.
2. Площадь синего прямоугольника равна: 5 х 5 = 25 см.
3. Таким образом, зелёный прямоугольник имеет площадь 25 + 14 = 39 см.
4. Площадь большого прямоугольника 78, то есть в два раза больше чем общая площадь маленьких (78 : 39 =2).
4. Поскольку зелёный прямоугольник и чёрный имеют одинаковую высоту, неизвестный отрезок должен быть в два раза больше ширины зелёного прямоугольника, то есть 2 x 5 = 10 см.
интересные математические задачи и задания
Математические задачи по возрасту
Заинтересовать дошкольников 5-7 лет, учащихся начальных классов проще всего. Главное — предложить разнообразные занимательные задания, сделать процесс решения задач увлекательным, с элементами игры, и обеспечить умеренную сложность задач.
Примеры заданий по возрасту
К 3-4 классу мотивация у школьника часто снижается. Родителям важно не упустить этот момент и объяснить ребёнку, зачем вообще заниматься математикой и учиться решать задачи.
Логико-математические и другие развивающие игры по возрасту
Занимательные задачи по типу
В плане регулярных тренировок в любом возрасте должно быть выполнение заданий минимум 5-7 типов. Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических способностей.
Среди самых интересных и популярных категорий заданий на логику и смекалку:
- Классические логические задачи. Учат детей анализировать текст, выделять главное, рассуждать и делать выводы.
- Арифметические ребусы. Отличная отработка ключевых мыслительных операций: абстрагирование, анализ и синтез, сравнение и другие.
- Задачи на закономерности, последовательности. Помогают развить аналитические способности и творческое мышление.
Примеры заданий по типу
японских математических секретов
Математика никогда не была моей сильной стороной в школе. Числа никогда не танцевали в линию для меня. Поэтому я подумал, что попытка разобраться с числами на иностранном языке будет невозможна. Однако, к моему большому удивлению, иметь дело с числами на японском было проще, чем я ожидал. Это было не из-за какого-то гения с моей стороны. Это полностью из-за гениальности самой японской системы подсчета.
Один, Два, Три, 一 、 二 、 三
Источник: СесилияВо-первых, японская система подсчета легко пугает.На самом деле, вы не должны беспокоиться. Вы уже освоили гораздо более сложную систему счисления. Подсчет на японском намного более логичен и систематичен, чем на английском. Если вы сможете овладеть основами, вы скоро полетите.
Давайте посмотрим на эти основы и что мы можем с ними сделать.
1: 一 ichi
2: 9 ni
3: Сан
4: / ши / йон
5: 五 го
6: 六 roku
7: ana Нана / Шичи
8: 八 хати
9: 九 ку
10: 十 жу
Первые десять номеров.Они не слишком пугающие, они. Всего десять цифр (двенадцать, если вы посчитаете два альтернативных способа сказать 4 и 7.) Стоит также изучить кандзи, если только вы можете читать цены в модных ресторанах соба. Я не знаю почему, но места соба рядом со мной всегда использовали цифры кандзи.
Теперь здесь японский язык имеет огромное преимущество перед английским. Числа от 11 до 99 используют те же звуки, которые вы только что наклонили. В отличие от английского с его странными исключениями из его собственных правил. Одиннадцать! О чем это все, а ?! Одиннадцать! Это не звучит так, как десять, один или даже двенадцать.
Есть очень много исключений, которые делают английскую систему счёта запутанной, особенно для маленьких детей. Но посмотрите на японцев за 11, 十一 juu-ichi, десять-один. Как красиво! Та же картина продолжается. 21 二十 一 ni-juu-ichi, два десять один. Как только вы дойдете до 100, вам нужно только выучить еще одно слово: хяку 百 . Теперь вы можете считать от 1 до 999, используя ту же систему. 101 — это 百一 hyaku-ichi. 241 — это 二百 四十 一 ни-хяку-йон-жуу-ичи.Единственное, на что вам следует обратить внимание — это звук хяку, превращающийся в бяку. Чтобы сосчитать от 1 до 9999, все, что вам нужно, это еще одно слово: , сен , , , , , , что означает тысячу. 10000 — это человек, , , , , , и применяются те же правила. Если вам интересно, 100 000 000 — это , оку , , , , , 1 000 000 000 000, , , , , , и 10 000 000 000 000 000, , .
Если вы живете в Японии, вам будет очень легко практиковаться в подсчете до тысяч, потому что это так часто случается, когда вы ходите по магазинам. 1000 иен это всего около 8 долларов США. Поскольку Япония является таким обществом, основанным на наличных деньгах, вы скоро будете ежедневно иметь дело с цифрами в тысячи и десятки тысяч. Когда я купил свою машину за наличные, я с удовольствием отсчитал the и 千.
Разумные системы именования в японской математике выходят за рамки самих чисел.Имена форм не требуют от вас изучения древнегреческого языка, как это делают английские. Теперь я большой любитель английской этимологии, но есть кое-что, что можно сказать о такой простой системе, как эта. Чтобы назвать многоугольник на японском языке, все, что вам нужно сделать, это сосчитать стороны и добавить это число к 900 или kakukei 角形 . Таким образом, треугольник — это санкаккеев 三 角形 , а восьмиугольник — хатикакукеи 八40 は4040 ) 角形 .По общему признанию, вам придется потратить некоторое время на изучение того, какое произношение 角形 идет с каждым числом.
Знаете ли вы, что такое односторонняя форма на английском языке? Можете ли вы решить, что это на японском?
Если вы сказали «hendecagon» и « juuichi kakukei 900一 角形 », то я приветствую ваши знания. Что было легче выяснить?
все делают куку
Источник: Брайан ОчаллаКуку не птица.Это инструмент для изучения таблиц умножения. Я помню, как боролся со своими временными таблицами в школе. Даже сейчас я боюсь, что меня попросят умножить числа на месте. Это не страх, который есть у многих японцев. С семи лет дети изучают свои временные таблицы, используя пение куку. Это охватывает временные таблицы до 9 × 9, и именно здесь Куку получает свое имя. Изучая Куку наизусть, японские дети получают прочную основу для изучения математики. Я рассказал о том, насколько регулярна японская система подсчета, но Куку отходит от этой тенденции.Чтобы соответствовать ритму, многие числа произносятся в упрощенной форме. Например, хати иногда сокращается до га. Кроме того, Куку не поможет вам пройти 9 × 9. Удивило некоторых японских учителей, которых я знаю, что западные студенты учатся до 12 × 12.
Тем не менее, если вы хотите попробовать это сами, есть много видео, которые используют разные ритмы или песни, чтобы помочь обучить куку. Я бы порекомендовал скачать понравившуюся вам версию, слушать ее снова и снова и пытаться подпевать.
Запоминание математических понятий снова появляется в образовании японских детей.В старших классах средней школы можно ожидать запоминания таблиц тригонометрических функций, что немыслимо в Великобритании. Заслуги запоминания этих тем можно обсудить, но без обучения, которое предоставляет куку, было бы гораздо сложнее. Я хотел бы, чтобы была песня, эквивалентная куку на английском языке, которую я мог бы выучить наизусть. Недавно я пытался запомнить Куку, и должен сказать, что это намного веселее, чем я ожидал.
Можете ли вы быть мастером Соробан?
Источник: Джо ХауптСуществует еще один инструмент, который может помочь вам улучшить свои математические навыки, и в буквальном смысле это инструмент. Соробан 算盤 — это японские счеты. Вы можете подумать: «Почему она предлагает мне использовать счеты?» У вас есть научный калькулятор. Абакусы так пять веков назад. Но у соробана есть способность превратить вас в умственного арифметического мага.
Японские счеты разделены на две части. Верхняя часть имеет один шарик, и каждый представляет 5 единиц. Нижняя часть имеет четыре шарика, каждый из которых представляет 1 единицу.Чтобы прочитать счеты, вы только смотрите на бусинки, которые были вставлены в середину счеты, упираясь в перегородку. Это читается слева направо. Вы можете попробовать это самостоятельно, используя этот виртуальный соробан.
Наличие физического представления чисел и фактически движущихся шариков делает использование счётов проще и веселее для детей, чем просто работа с суммами на бумаге. Цель состоит в том, чтобы использовать счеты в сочетании с мышечной памятью для механизации арифметического процесса. Опытный пользователь соробана может выполнять вычисления гораздо быстрее, чем кто-либо с электронным калькулятором, потому что им даже не нужно думать о вычислениях.Использование соробана становится автоматическим. Школы Соробана пользуются популярностью джуку 塾 , где дети обучаются навыкам абаки после школы. Существует даже проверенная система ранжирования, как в боевых искусствах. Я с удивлением наблюдал, как учитель, который сидел напротив меня, подсчитывал огромные суммы на соробане. Ее пальцы скользили по бусам с удивительной скоростью. Она также использовала его для добавления оценок на тестах. Я медленнее, неуклюже и менее точно делал то же самое с электрическим калькулятором.
Самым великим пользователям соробана перед ними даже не нужен соробан. Это называется anzan soroban 暗算 ん ろ ん ん или ментальный соробан. Люди, освоившие Анзан Соробан, усвоили счеты. Они могут видеть это в своем воображении. Если вы наблюдаете, как кто-то вычисляет с помощью anzan soroban, иногда вы увидите, как его пальцы щелкают, как будто они двигают бусинки на своих счетах, даже если их нет.Студенты сохраняют механизированный аспект соробана, поэтому им не нужно сознательно выполнять вычисления, чтобы получить правильный ответ. Посмотрите это видео о детях, играющих в ширитои (игра в слова) и одновременно делающих анзан соробан.
Это невероятно! Но самая впечатляющая форма Анзан Соробан еще более удивительна. Флэш Анзан является иллюстрацией необычайной силы человеческого мозга. Флэш-анзан был изобретен учителем соробан Йоджи Миямото как игра для растягивания учеников.Во вспышке anzan 15 чисел от 100 до 999 высвечиваются на экране. Задача состоит в том, чтобы добавить их в вашу голову. Хорошо, это звучит довольно сложно, но выполнимо, верно? Ну, чемпионы флэш-анзана могут сделать это менее чем за 2 секунды. Такео Сасано, чемпион 2012 года по всероссийскому флеш-анзану, прибавил 15 трехзначных чисел за 1,70 секунды. Вот видео Всеяпонского национального чемпионата по соробану в 2012 году, где участники делают расчет за 1,85 секунды.
Это сила Соробана.
Математика в Японии веселее
Источник: Pink Sherbet PhotographyПри работе с числами в Японии, безусловно, возникают сложности Подсчет вещей, а не только чисел, приводит вас в сложный мир японских счетчиков. На протяжении всей этой статьи я использовал чтение чисел on’yomi (ichi, ni, san и т. Д.), А не чтение kun’yomi (hitotsu, futsu, mittsu и т. Д.), Что является совершенно другим испытанием для мастера. ,
Однако, трудно или нет, я считаю, что есть что-то более важное, когда дело доходит до арифметического успеха.Это отношение. Когда я спросил своих японских студентов, какой у них любимый предмет, было примерно 60/40 разницы между физикой и математикой. Японские студенты, как правило, гораздо более уверены в математике, чем в английском. В то время как мои учителя по математике возвращались домой, мне отчаянно нравились учителя по математике в Японии. Меня часто приглашали в класс по математике, и учителя старались что-то объяснить на английском языке, во многом для развлечения студентов. На уроке математики я видел учеников, которых я знал как застенчивых и замкнутых, с удовольствием болтал о математических понятиях, которые были далеко от меня.Отношение к математике в Японии гораздо более позитивное, чем в Великобритании. Математика — это то, с чем можно поиграть в Японии. Неудивительно, что Япония является источником многих самых популярных в мире игр с числами, таких как судоку.
Несмотря на то, что вы и я никогда не достигнете полной математической беглости на японском языке и сможете выполнять массивные вычисления менее чем за две секунды, мы можем выучить не только математику на японском языке, но и положительное отношение Японии к нему.
,Что такое математика? | Живая наука
Математика — это наука, которая занимается логикой формы, количества и расположения. Математика вокруг нас, во всем, что мы делаем. Это строительный блок для всего в нашей повседневной жизни, включая мобильные устройства, архитектуру (древнюю и современную), искусство, деньги, инженерию и даже спорт.
С самого начала истории человечества математические открытия были в авангарде каждого цивилизованного общества и используются даже в самых примитивных культурах.Потребности в математике возникли исходя из потребностей общества. Чем сложнее общество, тем сложнее математические потребности. Первобытным племенам нужно было немного больше, чем умение считать, но они также полагались на математику для расчета положения солнца и физики охоты.
История математики
Несколько цивилизаций — в Китае, Индии, Египте, Центральной Америке и Месопотамии — внесли свой вклад в математику, какой мы ее знаем сегодня. Шумеры были первыми, кто разработал систему подсчета.Математики разработали арифметику, которая включает в себя основные операции, умножение, дроби и квадратные корни. Шумерская система прошла через Аккадскую империю к вавилонянам около 300 г. до н.э. Спустя шестьсот лет в Америке майя разработали сложные календарные системы и стали искусными астрономами. Примерно в это же время была разработана концепция нуля.
По мере развития цивилизаций математики начали работать с геометрией, которая вычисляет площади и объемы для угловых измерений и имеет множество практических применений.Геометрия используется во всем, от строительства дома до моды и дизайна интерьера.
Геометрия шла рука об руку с алгеброй, изобретенной в девятом веке персидским математиком Мухаммедом ибн-Мусой аль-Ховаризми. Он также разработал быстрые методы умножения и погружения чисел, которые известны как алгоритмы — искажение его имени.
Алгебра предложила цивилизациям способ разделить наследство и распределить ресурсы. Изучение алгебры означало, что математики решали линейные уравнения и системы, а также квадратики и изучали положительные и отрицательные решения.Математики в древние времена также начали смотреть на теорию чисел. Теория чисел берет свое начало в построении формы, рассматривая образные числа, характеристику чисел и теоремы.
Математика и греки
Изучение математики в ранних цивилизациях было строительным материалом для математики греков, которые разработали модель абстрактной математики через геометрию. Греция с ее невероятной архитектурой и сложной системой управления была образцом математических достижений до наших дней.Греческие математики были разделены на несколько школ:
- Ионийская школа , основанная Фалесом, которому часто приписывают первые дедуктивные доказательства и разработку пяти основных теорем в геометрии плоскости.
- Пифагорейская школа , основанная Пифагором, который изучал пропорции, плоскую и твердую геометрию и теорию чисел.
- Элеатическая школа , в которую входил Зено Элеа, известный своими четырьмя парадоксами.
- Софийская школа , которая зачисляется за предоставление высшего образования в передовых греческих городах.Софисты давали инструкции по публичным дебатам, используя абстрактные рассуждения.
- Школа Платона , основанная Платоном, который поощрял исследования в области математики в обстановке, очень похожей на современный университет.
- Школа Евдокса , основанная Евдоксом, который разработал теорию пропорциональности и величины и создал много теорем в геометрии плоскости.
- Школа Аристотеля , также известная как Лицей, была основана Аристотелем и следовала за Платоническая школа.
В дополнение к греческим математикам, перечисленным выше, ряд греков оставил неизгладимый след в истории математики. Архимед, Аполлоний, Диофант, Паппус и Евклид все пришли из этой эпохи. Чтобы лучше понять последовательность и то, как эти математики влияли друг на друга, посетите этот график.
За это время математики начали работать с тригонометрией. Вычислительная по своей природе тригонометрия требует измерения углов и вычисления тригонометрических функций, которые включают синус, косинус, тангенс и их обратные значения.Тригонометрия опирается на синтетическую геометрию, разработанную такими греческими математиками, как Евклид. Например, теорема Птолемея дает правила для хорды суммы и разности углов, которые соответствуют формулам суммы и разности для синусов и косинусов. В прошлых культурах тригонометрия применялась в астрономии и для вычисления углов в небесной сфере.
После падения Рима развитие математики взяли на себя арабы, а затем европейцы. Фибоначчи был одним из первых европейских математиков и был известен своими теориями по арифметике, алгебре и геометрии.Ренессанс привел к успехам, которые включали десятичные дроби, логарифмы и проективную геометрию. Теория чисел была значительно расширена, и такие теории, как вероятность и аналитическая геометрия, открыли новую эру математики с исчислением на переднем крае.
Развитие исчисления
В 17 веке Исаак Ньютон и Готфрид Лейбниц независимо разработали основы для исчисления. Развитие исчисления прошло три периода: ожидание, развитие и строгость.На стадии ожидания математики пытались использовать методы, которые включали бесконечные процессы, чтобы найти области под кривыми или максимизировать определенные качества. На стадии разработки Ньютон и Лейбниц свели эти методы вместе через производную и интегральную. Хотя их методы не всегда были логически обоснованы, математики в 18-м веке вышли на этап ригоризации и смогли их обосновать и создать заключительный этап исчисления. Сегодня мы определяем производную и интегральную с точки зрения ограничений.
В отличие от исчисления, являющегося типом непрерывной математики, другие математики выбрали более теоретический подход. Дискретная математика — это раздел математики, который имеет дело с объектами, которые могут принимать только отдельные, отдельные значения. Дискретные объекты могут быть охарактеризованы целыми числами, тогда как непрерывные объекты требуют действительных чисел. Дискретная математика является математическим языком информатики, так как включает в себя изучение алгоритмов. Области дискретной математики включают комбинаторику, теорию графов и теорию вычислений.
Люди часто задаются вопросом, какое значение имеют математики сегодня. В современном мире математика, такая как прикладная математика, не только актуальна, но и важна. Прикладная математика — это отрасли математики, которые участвуют в изучении физического, биологического или социологического мира. Идея прикладной математики заключается в создании группы методов, которые решают проблемы в науке. Современные области прикладной математики включают математическую физику, математическую биологию, теорию управления, аэрокосмическую инженерию и математические финансы.Прикладная математика не только решает проблемы, но и обнаруживает новые проблемы или развивает новые инженерные дисциплины. Прикладные математики требуют опыта во многих областях математики и науки, физической интуиции, здравого смысла и сотрудничества. Общий подход в прикладной математике состоит в том, чтобы построить математическую модель явления, решить модель и разработать рекомендации по улучшению производительности.
Хотя чистая математика не обязательно противоположна прикладной математике, она руководствуется абстрактными проблемами, а не проблемами реального мира.Многое из того, что преследуют чистые математики, может корениться в конкретных физических проблемах, но более глубокое понимание этих явлений приводит к проблемам и техническим аспектам. Эти абстрактные проблемы и технические особенности — это то, что пытается решить чистая математика, и эти попытки привели к крупным открытиям для человечества, включая Универсальную Машину Тьюринга, теоретизированную Аланом Тьюрингом в 1937 году. Универсальная Машина Тьюринга, которая началась как абстрактная идея, позже заложил основу для развития современного компьютера.Чистая математика абстрактна и основана на теории, и поэтому она не ограничена ограничениями физического мира.
Согласно одному чистому математику, чистые математики доказывают теоремы, а прикладные математики строят теории. Чистые и прикладные не являются взаимоисключающими, но они уходят корнями в разные области математики и решения проблем. Хотя сложная математика, связанная с чистой и прикладной математикой, не поддается пониманию большинства обычных американцев, решения, разработанные на основе этих процессов, повлияли на жизнь всех людей и улучшили ее.
,




