Сумма 3 слагаемых: Сумма трёх и более слагаемых
Сумма трёх и более слагаемых
Дата публикации: .
Сумма трех и более слагаемых
Слышите, звенит звонок!Начинается урок!
Поскорей проверь, дружок,
Все на месте ли тетрадки,
Книжки, ручки… Всё в порядке?
Ребята, сегодня мы с вами отправимся в увлекательное путешествие – в страну Математика. Там мы узнаем много интересного!
Страна Математика очень интересная! Вам обязательно в ней понравится! Но, путь туда не прост. И чтобы до неё добраться, вам нужно будет преодолеть преграды, решая примеры и задачи. Готовы? Тогда в путь!
1) Число 6 увеличьте в 5 раз.
2) Сумма двух чисел равна 25, одно слагаемое равно 5. Чему равно другое слагаемое?
3) Произведение двух чисел равно 20, один множитель равен 4. Чему равен другой множитель?
4) Делимое равно 35, делитель равен 5. Чему равно частное?
Примеры все решены!
И дорога в Страну Математика ведёт.
Но опасность снова ждёт.
Застряли цифры на болоте.
Освободим их поскорей.
Задачи надо правильно решить,
и дальше поспешить!
1) Напекла лиса ватрушек, пригласила 6 подружек. Вот ватрушки! Надо их разделить на … Всех ватрушек 36. Сколько каждой можно съесть?
2) В поле бабочки летали, лепестки цветов считали. На одном цветке их 6. Сколько будет лепестков, если 7 всего цветов?
3) Три песца в норе дремали, 5 пришли, их растолкали. Предложили на обед 7 отличнейших котлет. Я спрошу у умных деток: Сколько съедено котлеток?
Задачки правильно решили! Молодцы!
Чтобы пойти дальше, мы должны научиться складывать 3 числа.
Давайте посмотрим на выражение
6+(8+4) =
Решить устно этот пример не так просто. А вот в Стране Математике знают секреты, которые помогают легко и быстро находить значения таких выражений. Давайте разгадаем эти секреты.
При решении таких математических выражений можно использовать переместительное и сочетательное свойства сложения.
Выражение 6+(8+4)= можно записать так:
6+(8+4)=6+(4+8)
Какое свойство сложения использовалось? Правильно, переместительное свойство.В общем виде переместительное свойство сложения можно записать так:
а + в = в + а
При решении этого примера можно применить сочетательное свойство сложения. Запомните: чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего чисел.
(а+в)+с= а+(в+с)
Какими способами можно найти значение выражения 6+(8+4)?
1) Сложить числа 8 и 4 и к результату прибавить число 6.
2) Сложить числа 4 и 6 и к числу 8 прибавить результат.
3) Сложить числа 6 и 4 и к числу 8 прибавить результат.
4) Сложить числа 8 и 6 и к результату прибавить число 4.
Вот какие замечательные свойства арифметического действия сложения мы узнали в Стране Математика!
Давайте запишем наше выражение без скобок
6+(8+4)= 6+8+4.
Такие выражения называют суммой трёх слагаемых. Расстановка скобок не влияет на значение этого выражения. Сложение можно выполнять в любом удобном порядке.
Расстановка скобок не влияет на значение этого выражения. Сложение можно выполнять в любом удобном порядке.Ребята, решите примеры:
36+25+64=
54+22+98=
12+38+25=
51+39+34=
44+43+36=
узнали много нового!
И вот звенит звонок!
Всем отдыхать пора!
Спасибо за урок!
Сумма трех слагаемых | Computerworld Россия
Macworld.com
По мнению аналитиков, приобретение Pixar Animation Studios станет ключом к дальнейшему успешному развитию Disney
| Увидим ли мы полнометражный игровой фильм производства компании Disney в iTunes Music Store? |
Покупка компанией Disney за 7,4 млрд. долл. студии Pixar Animation Studios может ее укрепить связи с другой компанией, также возглавляемой Стивом Джобсом. Так считают эксперты, которых опросили журналисты Macworld. Компания Apple от объединения Disney и Pixar может выиграть во многом — от увеличения объема контента, предлагаемого через iTunes Music Store и до расширения использования ее компьютерных систем в одной из ведущих мировых киностудий.
Так считают эксперты, которых опросили журналисты Macworld. Компания Apple от объединения Disney и Pixar может выиграть во многом — от увеличения объема контента, предлагаемого через iTunes Music Store и до расширения использования ее компьютерных систем в одной из ведущих мировых киностудий.
«Disney одной из первых стала поддерживать усилия, предпринимаемые Apple на видеорынке», — отметил Росс Рубин, ведущий аналитик NPD Group. Он также считает, что обе компании уже имеют хорошие деловые отношения, по крайней мере в том, что касается доставки контента.
Принадлежащая Disney телевизионная сеть ABC и кабельная сеть Disney Channel предлагают коммерческие услуги для iTunes Music Store с октября 2005 года, то есть с момента начала продаж здесь видео. С начала этого года магазин начал предлагать спортивные передачи канала ESPN.
Приобрение Pixar позволила Стиву Джобсу войти в совет директоров Disney и назначить Джона Лассетера из Pixar на пост нового креативного директора компании.
Даже сейчас влияние NeXT можно ощутить на уровне руководства Apple. Помимо самого Джобса, среди бывших сотрудников NeXT в Apple работают Эви Теваньян, директор по программной технологии, Бертранд Серлет, старший вице-президент по разработке программного обеспечения, и Джон Рубинштейн, старший вице-президент подразделения iPod.
В конце концов, операционная система компании NeXT стала основой для MacOS X. В некотором отношении, как считают аналитики, именно NeXT пришла на смену Apple. Может ли то же самое произойти с Disney?
«Не думаю, что генеральный директор Disney Боб Игер — это следующий Жил Амелио, — заметил Майкл Гартенберг, директор по исследованиям компании JupiterResearch. — Также я не думаю, что возможность возглавить Disney для Стива Джобса столь же заманчива, как возможность возглавить Apple. Но следует иметь в виду, что Стив Джобс теперь крупнейший акционер Disney. Он захочет защитить свои инвестиции и развивать компанию. И руководство Disney поступит разумно, если будет прислушиваться к его советам».
Но следует иметь в виду, что Стив Джобс теперь крупнейший акционер Disney. Он захочет защитить свои инвестиции и развивать компанию. И руководство Disney поступит разумно, если будет прислушиваться к его советам».
Рубин считает, что приобретение Pixar станет ключом к дальнейшему успешному развитию Disney.
«Pixar имеет фантастический список побед — это далеко не одноразовый успех, — сказал он. — Совершенно очевидно, что дело здесь не только в технологии. Они пригласили писателей и сценаристов, которым удалось с большим успехом привлекать внимание зрителей, чем Disney».
Но что нас ждет дальше? Увидим ли мы полнометражный игровой фильм производства компании Disney в iTunes Music Store?
Пока Apple, продавая видео в Internet-магазине, ориентируется на короткометражные фильмы и телевизионные шоу. Рубин считает, что это обусловлено возможностями устройства, на котором воспроизводится этот контент. Соответственно, что по мере того, как пропускная способность Internet-каналов растет, а Apple разрабатывает все более совершенные и способные воспроизводить более качественное видео модели iPod, ситуация начнет меняться.
Однако Рубин предполагает, что любителей такого рода контента окажется значительно меньше, чем пользователей, которые смотрят телевизионные шоу и короткометражные фильмы. И эта ситуация создает серьезные проблемы таким компаниям, как Apple и Disney.
Присутствие Джобса в совете директоров Disney может заставить обе компании решать эту проблему.
«Если Apple, к примеру, станет более активно вести разработки компьютерных решений для домашних систем, то для таких компаний, как Disney, появление возможности добавлять дополнительный контент стало бы огромной победой», — сказал Рубин.
Со своей стороны Гартенберг уверен, что Apple и Disney очень хорошо дополняют друг друга.
Поделитесь материалом с коллегами и друзьями
Презентация «Сумма трех и более слагаемых»
Сумма трёх и более слагаемых
Слышите, звенит звонок! Начинается урок! Поскорей проверь, дружок,
Ребята, сегодня мы с вами отправимся в увлекательное путешествие – в страну Математика. Там мы узнаем много интересного!
Там мы узнаем много интересного!
Страна Математика очень интересная! Вам обязательно в ней понравится! Но, путь туда не прост. И чтобы до неё добраться, вам нужно будет преодолеть преграды, решая примеры и задачи. Готовы? Тогда в путь!
1) Число 6 увеличьте в 5 раз. 2) Сумма двух чисел равна 25, одно слагаемое равно 5. Чему равно другое слагаемое?
Примеры все решены. И дорога в Страну Математика ведёт. Но опасность снова ждёт. Застряли цифры на болоте. Освободим их поскорей. Задачи надо правильно решить, и дальше поспешить!
1) Напекла лиса ватрушек, пригласила 6 подружек. Вот ватрушки! Надо их разделить на …. Всех ватрушек 36. Сколько каждой можно съесть? 2) В поле бабочки летали, лепестки цветов считали. На одном цветке их 6. Сколько будет лепестков, если 7 всего цветов? 3) Три песца в норе дремали, 5 пришли, их растолкали. Предложили на обед 7 отличнейших котлет. Я спрошу у умных деток: Сколько съедено котлеток?
На одном цветке их 6. Сколько будет лепестков, если 7 всего цветов? 3) Три песца в норе дремали, 5 пришли, их растолкали. Предложили на обед 7 отличнейших котлет. Я спрошу у умных деток: Сколько съедено котлеток?
Задачки правильно решили! Молодцы! Чтобы пойти дальше, мы должны научиться складывать 3 числа.
Давайте посмотрим на выражение 6+(8+4)= Какие числа, и в каком порядке нужно складывать? Выполните вычисления.
Решить устно этот пример не так просто. А вот в Стране Математике знают секреты, которые помогают легко и быстро находить значения таких выражений. Давайте разгадаем эти секреты.
При решении таких математических выражений можно использовать переместительное и сочетательное свойства сложения.
Выражение 6+(8+4)= можно записать так: 6+(8+4)=6+(4+8) Какое свойство сложения использовалось? Правильно, переместительное свойство.
В общем виде переместительное свойство сложения можно записать так: а + в = в + а
При решении этого примера можно применить сочетательное свойство сложения. Запомните: чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего чисел. (а+в)+с= а+(в+с)
Какими способами можно найти значение выражения 6+(8+4) ? 1) Сложить числа 8 и 4 и к результату прибавить число 6 . 2) Сложить числа 4 и 6 и к числу 8 прибавить результат. 3) Сложить числа 6 и 4 и к числу 8 прибавить результат. 4) Сложить числа 8 и 6 и к результату прибавить число 4 .
Вот какие замечательные свойства арифметического действия «сложения» мы узнали в Стране Математика!
Давайте запишем наше выражение без скобок 6+(8+4)= 6+8+4. Выражение вида: 6+8+4 называют суммой трёх слагаемых.
Выражение вида: 6+8+4 называют суммой трёх слагаемых.
Расстановка скобок не влияет на значение этого выражения. Сложение можно выполнять в любом удобном порядке.
Ребята, решите примеры: 36+25+64= 54+22+98= 12+38+25= 51+39+34= 44+43+36=
Вы славно поработали, узнали много нового! И вот звенит звонок! Всем отдыхать пора! Спасибо за урок!
Методическая разработка урока математики (Начальная школа XXI века) по теме «Сумма трёх и более слагаемых»
Урок математики, 3 класс
(Начальная школа 21 века)
Учитель Василенко Светлана Фёдоровна
Тема урока. Сумма трёх и более слагаемых.
Цель урока: организовать совместную деятельность с целью отработки навыков сложения трёх и более слагаемых
Задачи урока: научить сознательному применению переместительного и сочетательного свойств сложения, отработать умение находить периметр многоугольников, длину ломаной линии, используя свойства сложения через решение примеров и задач.
УУД:
Личностные:
— формировать внутреннюю позицию школьника на уровне положительного отношения к школе; учебно-познавательные мотивы; учебно-познавательный интерес к новому материалу; способность к самооценке на основе критерия успешности учебной деятельности.
Метапредметные:
— познавательные: развивать умение самостоятельно выделять и формулировать познавательную цель; строить математическое высказывание в устной форме; выдвигать гипотезу; устанавливать причинно-следственные связи; делать обобщение; искать и выделять необходимую информацию; моделировать информацию.
— коммуникативные: формировать умение договариваться и приходить к общему решению в совместной деятельности; учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
— регулятивные: учить ставить новую учебную задачу в сотрудничестве с учителем; принимать и сохранять учебную задачу; осуществлять контроль по результату и способу действия.
Предметные:
Знать компоненты сложения, порядок выполнения примеров со скобками и без скобок.
Научиться находить значения выражений, где три и более слагаемых.
Совершенствовать вычислительные навыки, умение решать задачи, сравнивать выражения на основе сочетательного свойства сложения, группировать действия удобным способом.
Знать, что переместительное и сочетательное свойства сложения дают возможность записывать выражения, содержащие только сложение без скобок.
Уметь выполнять устные вычисления; объяснять решение; выполнять необходимые измерения и вычислять периметр прямоугольника разными способами.
Тип урока: открытие нового знания.
Формы организации познавательной деятельности:
Фронтальная работа, работа в парах, группах, самостоятельная работа, работа с учеником.
Используемые методы:
Объяснительно — иллюстративный, репродуктивный, проблемная ситуация.
Принципы обучения:
Наглядность, научность, доступность, активность, связь теории с практикой, комплексное решение задач образования, воспитание и развитие.
Используемые средства обучения:
— учебник, рабочая тетрадь на печатной основе, ПК, проектор, презентация к уроку, чертёжные инструменты, листы формата А3, 8 фигур (многоугольники).
Конечный результат и система контроля.
Индивидуальный контроль учителя и самопроверка, самоконтроль.
Ход урока
1. Этап мотивации (самоопределения) к учебной деятельности
Класс наш светлый и уютный,
Хорошо мы в нём живём.
Улыбнёмся же друг другу
И урок скорей начнём.
2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.
Устная разминка:
Слайд 1.
а) — Прочитайте числа: 24, 756, 200, 88, 391, 542, 817, 45, 420.
— На какие группы их можно разбить? (круглые, чётные, нечётные,…)
Слайд 2.
б) — Устно продолжите ряды чисел, разгадав правило, по которому они записаны:
100, 90, 80, 70,…,…на доске
50, 100, 150, 200,…,…на доске
991, 981, 971, 961,…,…на доске
— А теперь послушайте загадку и определите тему урока.
Числа плюсом прибавляем
И ответ потом считаем.
Если «плюс», то, без сомнения,
Это действие — … (сложение)
— Тема урока «Сложение».
— Действительно, говорить на нашем уроке мы будем о сложении.
— Я сейчас проведу блиц-опрос, и посмотрю, как вы ориентируетесь в этой теме.
Блиц—опрос
1. Как называются компоненты действия сложения»? (1 слагаемое, 2 слагаемое)
2. Как называется результат действия сложения? (сумма)
3. Какое математическое действие является обратным действию сложения?
4. Что записано на карточках? (выражения)
Слайд 3.
а+ b a+(b+c)
b+a (a+b)+c
5. Какие вы видите выражения: числовые или буквенные? (буквенные)
6. Какие свойства сложения вы знаете?
7. Какая буквенная запись соответствует переместительному свойству, а какая сочетательному свойству сложения?
3. Формулировка темы и цели урока. Практическая работа.
Слайд 4.
Задание:
— Начертите ломаную линию в тетради по заданным параметрам: первое звено — 6 см, второе — 3 см, третье — 4 см, четвёртое — 7 см. Найдите длину ломаной линии. (Один ученик у доски) 6+3+4+7
(Один ученик у доски) 6+3+4+7
— Можно ли по-другому вычислить длину ломаной?
— Как удобнее будет считать? 6+3+4+7=6+4+3+7
— Каким свойством сложения воспользовались?
— Вот мы и столкнулись с заданием, которое нам поможет уточнить тему урока и сформулировать цель урока.
Слайд 5.
— Тема урока: «Сложение трёх и более слагаемых»
— Цель: научиться находить значения выражений, где три и более слагаемых.
4. Изучение нового материала (работа в тройках)
Слайд 6.
— Рассмотрим картинку на стр. 65 учебника, она же есть и на слайде.
— Итак, давайте сначала разберемся, как ВОЛК получил каждое выражение в цепочке, каким именно свойством сложения он пользовался каждый раз.
— Объясните, как получилось выражение 9+(4+6), каким свойством воспользовался ВОЛК?
(Сочетательным свойством сложения; в данном случае, чтобы к сумме 9 и 4 прибавить 6, можно к числу 9 прибавить сумму 4 и 6).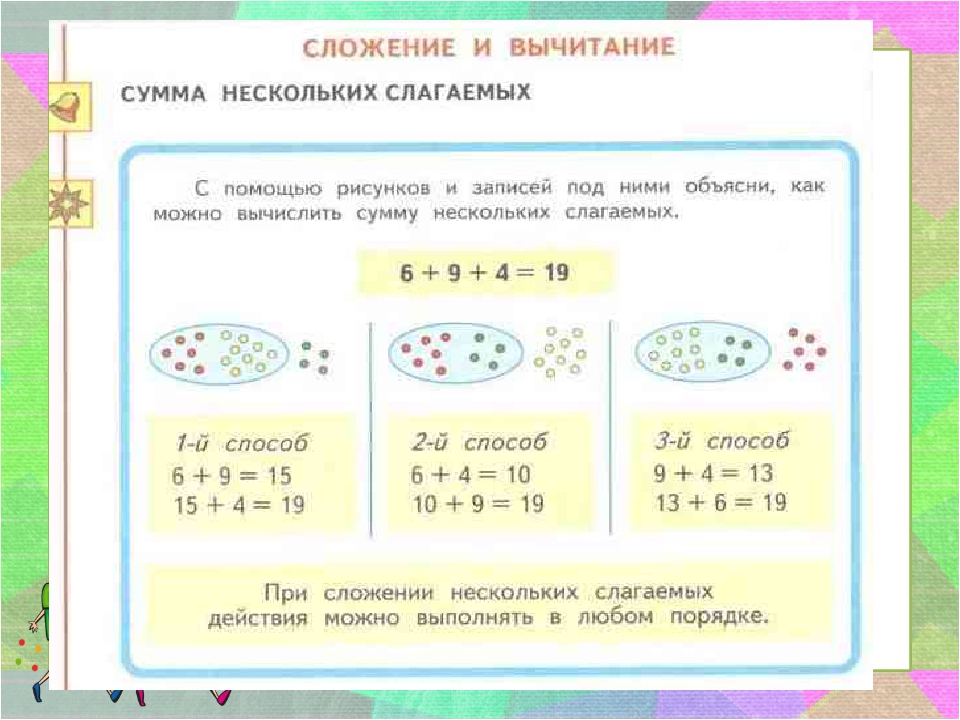 Это и написал ВОЛК во второй строке.
Это и написал ВОЛК во второй строке.
— А как получилось выражение 9+(6+4)? Какое свойство использовалось? К каким числам оно применено?
(ВОЛК применил переместительное свойство сложения к числам 4 и 6, он их переставил и получил 6 и 4).
— Объясните, как получилось выражение (9+6) +4.
(К выражению 9+(6+4) ВОЛК применил сочетательное свойство сложения, только с «конца», переставив части формулировки свойства).
Теперь давайте проанализируем, что же у нас получилось. Какими способами можно найти значение выражения (9+4)+6?
Сложить 9 и 4 и к результату прибавить 6.
Сложить 4 и 6 и к числу 9 прибавить результат.
Сложить 6 и 4 и к числу 9 прибавить результат.
Сложить 9 и 6 и к результату прибавить 4.
— А теперь рассмотрим, как действовал ЗАЯЦ. Выражение (9+4)+6 представляет сумму 9+4 и 6. Какое первое слагаемое в этом выражении? (9+4).
Выражение (9+4)+6 представляет сумму 9+4 и 6. Какое первое слагаемое в этом выражении? (9+4).
— Какое второе? (6)
— На основании какого свойства получилось выражение 6+(9+4)?
( На основании переместительного свойства: слагаемые 9+4 и 6 ЗАЯЦ переставил).
— Объясните, как получилось выражение (6+9)+4?
— Объясните, как получилось выражение 4+(6+9)?
— Прочитайте текс в рубрике «Обрати внимание» на стр.65 учебника.
— Выражение, с которым мы работали, я запишу без скобок 9+4+6. Это выражение называют суммой трёх слагаемых.
— К какому выводу мы с вами пришли?
(Различные расстановки скобок не влияют на значение этого выражения. Перестановка любых чисел в сумме и их удачная группировка позволяют выбрать наиболее быстрый способ сложения)
— Как в таком случае можно выполнять сложение? (В любом порядке)
5. Физкультминутка
Физкультминутка
Слайд 7-8.
— для глаз
Слайд 9-10.
— в движении (называют числа и выполняют движения)
Слайд 11.
Продолжение изучения нового материала (2 человека работают у доски с другими ценниками (12р., 8р., 16р., 5р., 15р., 4р.; 11р., 3р.. 7р., 13р., 18р.,2р.))
— Скажите, а так ли уж нам необходима эта тема?
— Где в повседневной жизни мы с ней сталкиваемся? (Дети рассуждают.)
— Давайте представим, что мы совершаем покупку в магазине. В магазине мы все видим этикетки, на которых написана цена товара, (на доске «ценники»)
25р. 45р. 72р. 28р. 64р. 36р.
— Все эти товары вам необходимо купить! Что вы скажете про их количество? (их много).
— За вами огромная очередь, продавец тоже спешит. Как вы будете считать стоимость своих покупок, чтобы не задерживать ни покупателей, ни продавца? У вас при себе есть только 300р. (Использовать сочетательное и переместительное свойство сложения.)
(Использовать сочетательное и переместительное свойство сложения.)
— В тетрадь запишите выражение, с помощью которого можно быстро узнать стоимость всего товара.
— Так нужна ли в жизни наша сегодняшняя тема: сложение трех и более слагаемых?
6. Построение проекта выхода из затруднения. Самостоятельная работа.
Слайд 12-13.
— Перед вами – пример 1+2+3+4+5+6+7+8+9= (на слайде). Пример длинный. На его решение может уйти немало времени. Попробуйте, найти быстрое его решение, можете посоветоваться с соседом по парте.
1+2+3+4+5+6+7+8+9= (1+9)+(2+8)+(3+7)+(4+6)=40 (один ученик выходит к доске, все проверяют в тетради)
— К какому выводу вы пришли? ( Чтобы решить пример на сложение с большим количеством слагаемых, нужно слагаемые переставлять, пользуясь переместительным свойством и группировать их, пользуясь сочетательным свойством).
— Итак, мы пришли к выводу, что при сложении нескольких чисел их можно как угодно объединять в группы и переставлять (что переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм).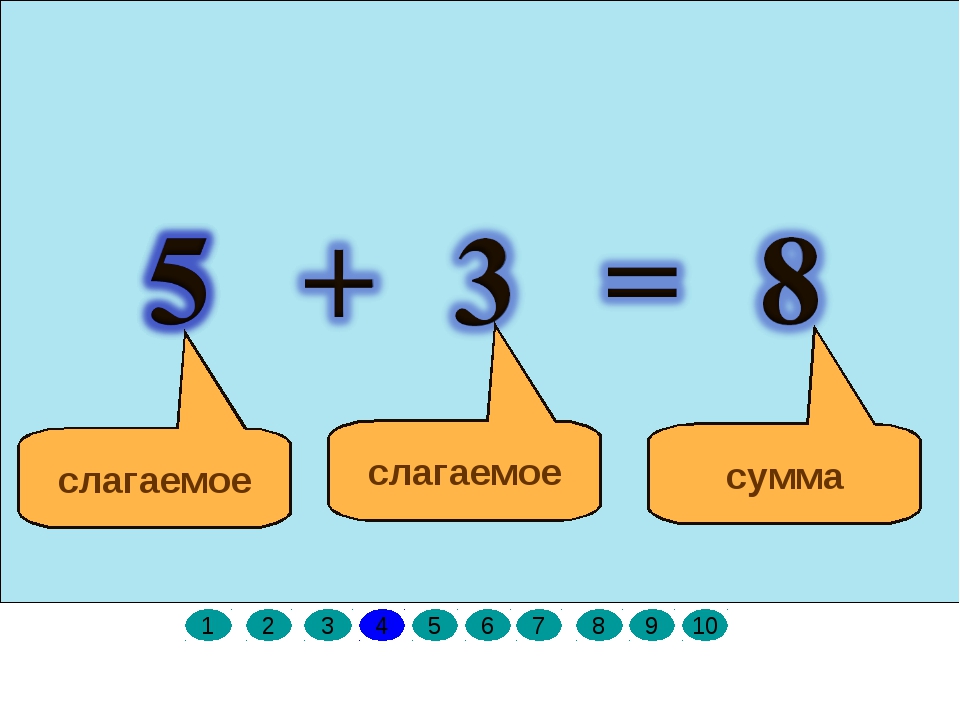
7. Практическая работа, запись дом. зад.
Слайд 14.
— Запишите, пожалуйста дом. зад. стр. 85 №6, 7.
— Продолжаем работать в группах, домашнее задание будет подобное, слушайте внимательно инструкцию.
— Каждой группе (8 групп) нужно выполнить необходимые измерения данных фигур (сиреневого и синего цвета), записать выражение для нахождения периметра и вычислить его значение удобным способом.
8. Самостоятельная работа. Работа в тетрадях на печатной основе
Слайд 15-16.
— Перед тем, как вы начнёте работать самостоятельно в тетради на печатной основе, проведём тест.
1. Как называется свойство сложения, если числа меняются местами?
а) Переместительное
б) Сочетательное
2. Как называется свойство сложения: (а + б) + с = а + (б + с) ?
а) Переместительное
б) Сочетательное
3. Какой термин лишний?
а) Слагаемое
б) Множитель
в) Сумма
4. Какое число лишнее?
Какое число лишнее?
а) 456
б) 76
в) 890
5. Что не относится к единицам длины?
а) Килограмм
б) Километр
в) Сантиметр
6. Как говорят про учеников, которые ответили на все вопросы теста правильно?
а) Удальцы
б) Молодцы
в) Хитрецы
Слайд 17.
— На стр. 37 №127, стр. 38 №128, 129.
— №130 задание на сложение трёхзначных чисел «столбиком» разной сложности. Выбрать и решить по силам один пример.
9. Рефлексия
Слайд 18.
Урок пора нам завершать.
Теперь должны мы вспомнить,
Что нового смогли узнать,
Что нужно нам запомнить.
— Какие математические свойства нам помогали на уроке находить сумму трёх и более слагаемых?
— Наш урок подходит к концу. Поделитесь своими впечатлениями.
(Дети проводят самооценку своей деятельности на уроке).
Слайд 19.
— Под марш выходим на перемену.
Научно-популярное ток-шоу для подростков «Сумма трех слагаемых» / События на TimePad.ru
Регистрация на событие закрыта
Извините, регистрация закрыта. Возможно, на событие уже зарегистрировалось слишком много человек, либо истек срок регистрации. Подробности Вы можете узнать у организаторов события.
Другие события организатора>
ИЦАЭ Новосибирск
1550 дней назад
17 ноября 2016 c 19:00 до 20:30
Новосибирск
Красный проспект, 82
Научно-популярное ток-шоу для подростков: три гостя, три науки, один предмет.
Расскажите друзьям о событии
В образовательном порту «Научилус» (Красный проспект, 82) пройдет первое подростковое научно-популярное ток-шоу «Сумма трех слагаемых», на которое мы ждем вас 17 ноября в 19:00. Темой первого шоу станут захватившие весь мир во второй раз покемоны сказочные «карманные» существа из Японии, которые из мультика про мальчика Эша переехали в наши мобильные телефоны и прочно там обосновались.
Покемонов с точки зрения своих научных интересов рассмотрят три гостя ток-шоу филолог Жанна Бордакова расскажет о секрете популярности этого явления, биолог Даниил Гладких разберется в их происхождении и эволюции, а физик Александр Ерастов объяснит, как устроены сверхспособности этих существ и как правильно выбрать покемона для боя.
Также наши гости с удовольствием ответят на ваши вопросы, авторы лучших вопросов получат подарки от Информационного центра по атомной энергии.
Чтобы найти слагаемое нужно правило. Вычитание натуральных чисел. Уменьшаемое, вычитаемое, разность
Слагаемое, сумма; уменьшаемое, вычитаемое, разностьЮргель Ольга Александровна
1 класс (1-4)
Цель:
- закрепить знание названий компонентов сложения и вычитания; продолжить работу по формированию прочных, осознанных, доведенных до автоматизма навыков вычислений в пределах 20;
- развивать математическую речь учащихся;
- воспитывать аккуратность при работе в тетради.
Оборудование: изображение инопланетян, буквы с примерами, линейка с рисунками и примеры к ней.
I Орг. момент.
II Устный счет.
Сегодня к нам на урок прилетели гости. Это необычные гости. Хотите отгадать, кто это? Для этого нужно решить примеры на карточках с буквами и поставить их по порядку под соответствующими числами:
Дети решают примеры на карточках (сложение и вычитание в пределах 20 с ответами от 1 до 12, в соответствии с таблицей). Читают появившееся слово: инопланетяне.
— Правильно! Это инопланетяне. А вот и они. (На доску прикрепляется изображение инопланетян.)
Приземление состоялось. Они пока еще не знают нашего языка и говорят со мной мысленно. Это называется телепатией. Они говорят мне, что хотят изучить Землю и людей. И они хотят познакомиться с вами.
Первое, что они хотят исследовать, это ваша сообразительность. Для этого они просят представить в виде десятков и единиц числа. А какие это числа, попробуем мысленно прочитать. Инопланетяне посылают нам сигнал. Ну-ка, кто угадает числа?
Ну-ка, кто угадает числа?
Дети называют числа, если число двузначное, значит, верно прочитали мысли. Число представляют в виде суммы разрядных слагаемых.
На планете, где живутнаши гости, вместо цифр используются другие значки. Посмотрите, они привезли с собой линейку:
а) Сравните числа: листочек и вишенка; груша и звездочка; морковка и флажок; солнышко и гриб.
Записываются неравенства с использованием данных значков.
б) Решите примеры:
Цветочек + 1
Морковка – 1
Треугольник + 2
Груша – 2
Вишенка – 2
Записывают примеры на доске.
А теперь давайте-ка покажем, как мы умеем решать наши земные примеры:
Дети решают примеры на счетных веерах.
III Работа над темой урока.
А теперь внимание, инопланетяне мысленно стараются помочь вам получше запомнить компоненты сложения. Как называются числа, которые мы складываем?(Слагаемые.)
Повторим хором.
Дети повторяют сначала тихо, потом все громче и громче.
Как называется результат сложения? (Сумма.)
Назовите слагаемые и сумму:
А теперь решите-ка вот этот пример:
Теперь почувствуйте, как ваша память снова включается. Почувствовали?
19 – это уменьшаемое.
Повторяют хором.
Как вы думаете, почему этот компонент так назвали? (Потому что это число будет меньше, когда вычтем.)
4 – это вычитаемое . (Хором)
Почему так называется? (Мы его вычитаем.)
А то, что получилось в результате – это разность . (Хором.)
IV Работа по учебнику.
Примеры № 4 (Дети работают в парах.)
Найдите примеры, где в результате должна получиться сумма. Запишите и решите любой. А теперь объясните соседу, где слагаемые, а где сумма.
Найдите примеры, где в ответе получится разность. Запишите и решите любой. Объясните соседу, где уменьшаемое, где вычитание, а где разность.
с. 55 № 4 – устно.
V
Работа в тетрадях.
№ 1 – решение задачи
№ 6 – самостоятельно (поставьте знаки >,
VI Итог урока.
А теперь, ребята, инопланетяне просят повторить вас, чем мы занимались сегодня на уроке, что повторяли?
Они привезли с собой пятерки, которые ставят в школах на их планете.
(Учитель раздает призы тем детям, которые были наиболее активны на уроке.)
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова «вычитаемое», «уменьшаемое», «разность». Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Данное понятие в математике означает:
- разницу между двумя числами;
- это показатель того, насколько одно количество больше или меньше другого;
- это результат, полученный при выполнении вычитания — такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | — | 11 | = | 7 |
| 14 | — | 5 | = | 9 |
| 26 | — | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
Так же и во всех подобных случаях:
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Понятие вычитания лучше всего рассмотреть на примере. Вы решили попить чай с конфетами. В вазе лежало 10 конфет. Вы съели 3 конфеты. Сколько конфет осталось в вазе? Если мы от 10 вычтем 3 то, в вазе останется 7 конфет. Запишем задачу математически:
Подробно разберем запись:
10 – это число от которого мы отнимаем или которое уменьшаем, поэтому его называют уменьшаемым .
3 – это число, которое мы вычитаем. Поэтому его называют вычитаемым .
7 – это число результат вычитания или еще его называют разностью . Разность показывает на сколько первое число (10) больше второго числа (3) или насколько второе число (3) меньше первого числа (10).
Если вы сомневаетесь правильно ли нашли разность, нужно сделать проверку . К разности прибавить второе число: 7+3=10
При вычитании л уменьшаемое не может быть меньше вычитаемого.
Делаем вывод из сказанного. Вычитание – это действие, с помощью которого по сумме и одному из слагаемых находится второе слагаемое.
В буквенном виде это выражение будет выглядеть так:
a — b = c
a – уменьшаемое,
b – вычитаемое,
c – разность.
Свойства вычитания суммы из числа.
13 — (3 + 4)=13 — 7=6
13 — 3 — 4 = 10 — 4=6
Пример можно решить двумя способами. Первый способ, найти сумму чисел (3+4), а потом вычесть от общего числа (13). Второй способ, от общего числа (13) вычесть первое слагаемое(3), а потом из полученной разности отнять второе слагаемое(4).
Второй способ, от общего числа (13) вычесть первое слагаемое(3), а потом из полученной разности отнять второе слагаемое(4).
В буквенном виде свойство вычитания суммы из числа будет выглядеть так:
a — (b + c) = a — b — c
Свойство вычитания числа из суммы.
(7 + 3) — 2 = 10 — 2 = 8
7 + (3 — 2) = 7 + 1 = 8
(7 — 2) + 3 = 5 + 3 = 8
Чтобы вычесть из суммы число, можно это число вычесть из одного слагаемого, а потом к полученному результату разности прибавить второе слагаемое. При условии слагаемое будет больше вычитаемого числа.
В буквенном виде свойство вычитания числа из суммы будет выглядеть так:
(7 + 3) — 2 = 7 + (3 — 2)
(a + b) — c= a + (b — с) , при условии b > c
(7 + 3) — 2=(7 — 2) + 3
(a + b) — c=(a — c) + b , при условии a > c
Свойство вычитания с нулем.
10 — 0 = 10
a — 0 = a
Если из числа вычесть нуль то, будет тоже самое число.
10 — 10 = 0
a — a = 0
Если из числа вычесть тоже самое число то, будет нуль.
Вопросы по теме:
В примере 35 — 22 = 13 назовите уменьшаемое, вычитаемое и разность.
Ответ: 35 – уменьшаемое, 22 – вычитаемое, 13 – разность.
Если числа одинаковые, чему равна их разность?
Ответ: нуль.
Сделайте проверку вычитания 24 — 16 = 8?
Ответ: 16 + 8 = 24
Таблица вычитания натуральных чисел от 1 до 10.
Примеры на задачи по теме «Вычитание натуральных чисел».
Пример №1:
Вставьте пропущенное число: а)20 — … = 20 б) 14 — … + 5 = 14
Ответ: а) 0 б) 5
Пример №2:
Можно ли выполнить вычитание: а) 0 — 3 б) 56 — 12 в) 3 — 0 г) 576 — 576 д) 8732 — 8734
Ответ: а) нет б) 56 — 12 = 44 в) 3 — 0 = 3 г) 576 — 576 = 0 д) нет
Пример №3:
Прочитайте выражение: 20 — 8
Ответ: “От двадцати отнять восемь” или “из двадцати вычесть восемь”.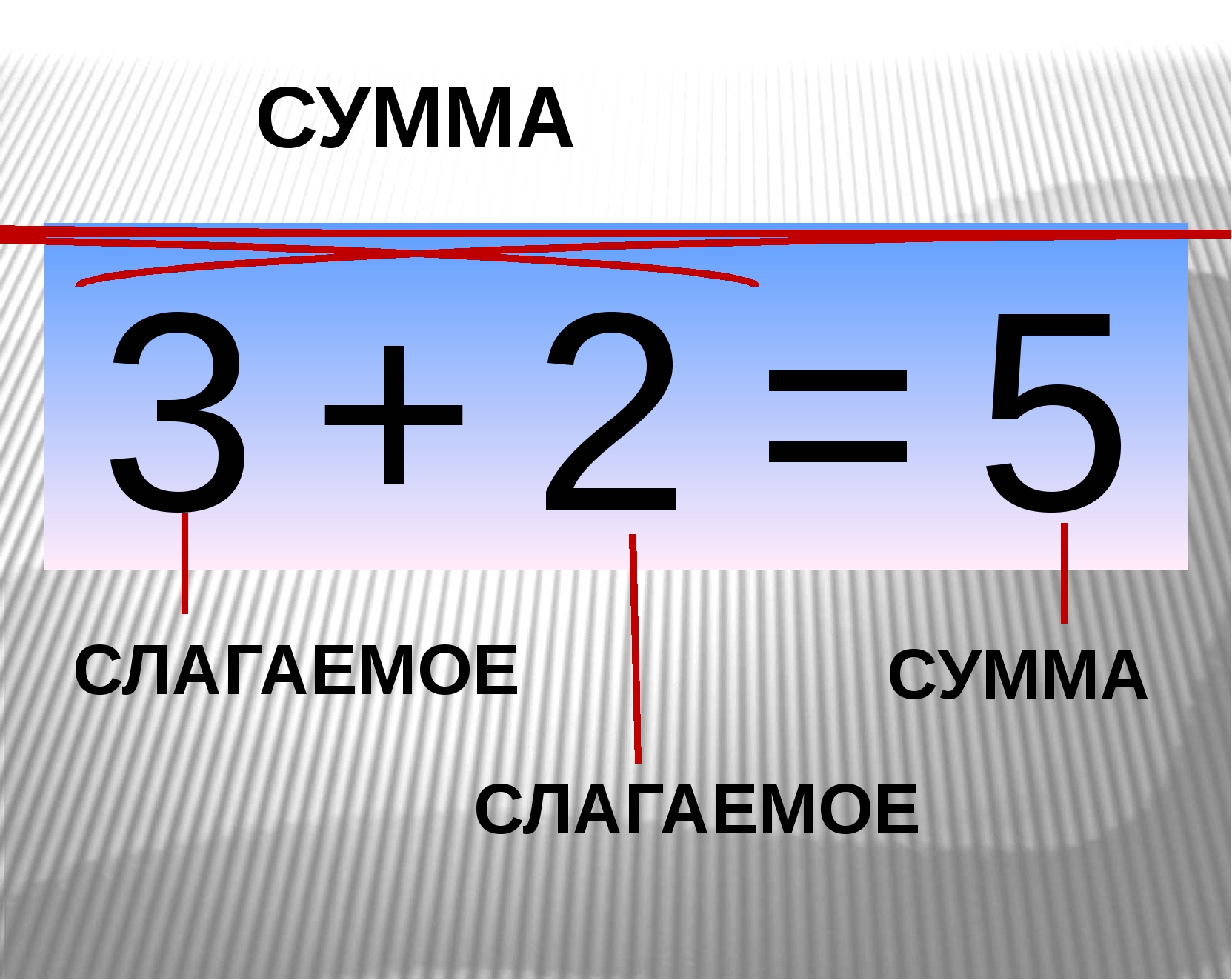 Правильно произносить слова
Правильно произносить слова
Долгий путь наработки навыков решения уравнений начинается с решения самых первых и относительно простых уравнений. Под такими уравнениями мы подразумеваем уравнения, в левой части которых находится сумма, разность, произведение или частное двух чисел, одно из которых неизвестно, а в правой части стоит число. То есть, эти уравнения содержат неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое или делитель. О решении таких уравнений и пойдет речь в этой статье.
Здесь мы приведем правила, позволяющие находить неизвестное слагаемое, множитель и т.п. Причем будем сразу рассматривать применение этих правил на практике, решая характерные уравнения.
Навигация по странице.
Итак, подставляем в исходное уравнение 3+x=8
вместо x
число 5
, получаем 3+5=8
– это равенство верное, следовательно, мы правильно нашли неизвестное слагаемое. Если бы при проверке мы получили неверное числовое равенство, то это указало бы нам на то, что мы неверно решили уравнение. Основными причинами этого могут быть либо применение не того правила, которое нужно, либо вычислительные ошибки.
Основными причинами этого могут быть либо применение не того правила, которое нужно, либо вычислительные ошибки.
Как найти неизвестное уменьшаемое, вычитаемое?
Связь между сложением и вычитанием чисел, про которую мы уже упоминали в предыдущем пункте, позволяет получить правило нахождения неизвестного уменьшаемого через известное вычитаемое и разность, а также правило нахождения неизвестного вычитаемого через известное уменьшаемое и разность. Будем формулировать их по очереди, и сразу приводить решение соответствующих уравнений.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Для примера рассмотрим уравнение x−2=5 . Оно содержит неизвестное уменьшаемое. Приведенное правило нам указывает, что для его отыскания мы должны к известной разности 5 прибавить известное вычитаемое 2 , имеем 5+2=7 . Таким образом, искомое уменьшаемое равно семи.
Если опустить пояснения, то решение записывается так:
x−2=5
,
x=5+2
,
x=7
.
Для самоконтроля выполним проверку. Подставляем в исходное уравнение найденное уменьшаемое, при этом получаем числовое равенство 7−2=5 . Оно верное, поэтому, можно быть уверенным, что мы верно определили значение неизвестного уменьшаемого.
Можно переходить к нахождению неизвестного вычитаемого. Оно находится с помощью сложения по следующему правилу: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность .
Решим уравнение вида 9−x=4 с помощью записанного правила. В этом уравнении неизвестным является вычитаемое. Чтобы его найти, нам надо от известного уменьшаемого 9 отнять известную разность 4 , имеем 9−4=5 . Таким образом, искомое вычитаемое равно пяти.
Приведем краткий вариант решения этого уравнения:
9−x=4
,
x=9−4
,
x=5
.
Остается лишь проверить правильность найденного вычитаемого. Сделаем проверку, для чего подставим в исходное уравнение вместо x
найденное значение 5
, при этом получаем числовое равенство 9−5=4
. Оно верное, поэтому найденное нами значение вычитаемого правильное.
Оно верное, поэтому найденное нами значение вычитаемого правильное.
И прежде чем переходить к следующему правилу заметим, что в 6 классе рассматривается правило решения уравнений, которое позволяет выполнять перенос любого слагаемого из одной части уравнения в другую с противоположным знаком. Так вот все рассмотренные выше правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого с ним полностью согласованы.
Чтобы найти неизвестный множитель, надо…
Давайте взглянем на уравнения x·3=12 и 2·y=6 . В них неизвестное число является множителем в левой части, а произведение и второй множитель известны. Для нахождения неизвестного множителя можно использовать такое правило: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель .
В основе этого правила лежит то, что делению чисел мы придали смысл, обратный смыслу умножения. То есть, между умножением и делением существует связь: из равенства a·b=c
, в котором a≠0
и b≠0
следует, что c:a=b
и c:b=c
, и обратно.
Для примера найдем неизвестный множитель уравнения x·3=12 . Согласно правилу нам надо разделить известное произведение 12 на известный множитель 3 . Проведем : 12:3=4 . Таким образом, неизвестный множитель равен 4 .
Кратко решение уравнения записывается в виде последовательности равенств:
x·3=12
,
x=12:3
,
x=4
.
Желательно еще сделать проверку результата: подставляем в исходное уравнение вместо буквы найденное значение, получаем 4·3=12 – верное числовое равенство, поэтому мы верно нашли значение неизвестного множителя.
И еще один момент: действуя по изученному правилу, мы фактически выполняем деление обеих частей уравнения на отличный от нуля известный множитель. В 6 классе будет сказано, что обе части уравнения можно умножать и делить на одно и то же отличное от нуля число, это не влияет на корни уравнения.
Как найти неизвестное делимое, делитель?
В рамках нашей темы осталось разобраться, как найти неизвестное делимое при известном делителе и частном, а также как найти неизвестный делитель при известном делимом и частном. Ответить на эти вопросы позволяет уже упомянутая в предыдущем пункте связь между умножением и делением.
Ответить на эти вопросы позволяет уже упомянутая в предыдущем пункте связь между умножением и делением.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Рассмотрим его применение на примере. Решим уравнение x:5=9 . Чтобы найти неизвестное делимое этого уравнения надо согласно правилу умножить известное частное 9 на известный делитель 5 , то есть, выполняем умножение натуральных чисел: 9·5=45 . Таким образом, искомое делимое равно 45 .
Покажем краткую запись решения:
x:5=9
,
x=9·5
,
x=45
.
Проверка подтверждает, что значение неизвестного делимого найдено верно. Действительно, при подстановке в исходное уравнение вместо переменной x числа 45 оно обращается в верное числовое равенство 45:5=9 .
Заметим, что разобранное правило можно трактовать как умножение обеих частей уравнения на известный делитель. Такое преобразование не влияет на корни уравнения.
Переходим к правилу нахождения неизвестного делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное .
Рассмотрим пример. Найдем неизвестный делитель из уравнения 18:x=3 . Для этого нам нужно известное делимое 18 разделить на известное частное 3 , имеем 18:3=6 . Таким образом, искомый делитель равен шести.
Решение можно оформить и так:
18:x=3
,
x=18:3
,
x=6
.
Проверим этот результат для надежности: 18:6=3 – верное числовое равенство, следовательно, корень уравнения найден верно.
Понятно, что данное правило можно применять только тогда, когда частное отлично от нуля, чтобы не столкнуться с делением на нуль. Когда частное равно нулю, то возможны два случая. Если при этом делимое равно нулю, то есть, уравнение имеет вид 0:x=0
, то этому уравнению удовлетворяет любое отличное от нуля значение делителя. Иными словами, корнями такого уравнения являются любые числа, не равные нулю. Если же при равном нулю частном делимое отлично от нуля, то ни при каких значениях делителя исходное уравнение не обращается в верное числовое равенство, то есть, уравнение не имеет корней. Для иллюстрации приведем уравнение 5:x=0
, оно не имеет решений.
Для иллюстрации приведем уравнение 5:x=0
, оно не имеет решений.
Совместное использование правил
Последовательное применение правил нахождения неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя позволяет решать и уравнения с единственной переменной более сложного вида. Разберемся с этим на примере.
Рассмотрим уравнение 3·x+1=7 . Сначала мы можем найти неизвестное слагаемое 3·x , для этого надо от суммы 7 отнять известное слагаемое 1 , получаем 3·x=7−1 и дальше 3·x=6 . Теперь осталось найти неизвестный множитель, разделив произведение 6 на известный множитель 3 , имеем x=6:3 , откуда x=2 . Так найден корень исходного уравнения.
Для закрепления материала приведем краткое решение еще одного уравнения (2·x−7):3−5=2
.
(2·x−7):3−5=2
,
(2·x−7):3=2+5
,
(2·x−7):3=7
,
2·x−7=7·3
,
2·x−7=21
,
2·x=21+7
,
2·x=28
,
x=28:2
,
x=14
.
Список литературы.
- Математика. . 4 класс. Учеб.
 для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.].- 8-е изд. — М.: Просвещение, 2011. — 112 с.: ил. — (Школа России). — ISBN 978-5-09-023769-7.
для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.].- 8-е изд. — М.: Просвещение, 2011. — 112 с.: ил. — (Школа России). — ISBN 978-5-09-023769-7. - Математика : учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
Чтобы найти неизвестное слагаемое, надо ………………………………………………………….. Результат умножения двух и более множителей называется………………………………………… Чтобы найти делимое, надо ……………………………………………………………………………… Результат вычитания чисел называется ………………………………………………………………… Результат сложения двух и более слагаемых называется ……………………………………… Чтобы найти неизвестный множитель, надо…………………………………………………………. Результат деления чисел называется…………………………………………………………………. Чтобы найти уменьшаемое, надо………………………………………………………………………… Чтобы найти делитель, надо……………………………………………………………………………… Чтобы найти вычитаемое, надо…………………………………………………………………………. Чтобы найти на сколько одно число больше или меньше другого, надо………………………….……………………………………………………………………………………………………………..Чтобы найти во сколько раз одно число больше или меньше другого, надо ……………………….…………………………………………………………………………………………………………………. В выражении без скобок, содержащем только сложение и вычитание или умножение и деление, действия выполняются ………………… ……………………………………………………………. В выражениях, содержащих скобки, сначала выполняются все действия ………………………..…………………………………………………………………………………………………………………………………………………………………………………………………………………………………….. Периметр фигуры – это ………………………………………………………………………………… Периметр прямоугольника равен ……………………………………………………………………… Периметр квадрата равен …………………………………………………………………………………………………. Полупериметр прямоугольника – это ………………………………………………………………….. Чтобы найти сторону квадрата, надо значение его периметра………………………………………… Чтобы найти площадь прямоугольника, надо …………………………………………………………… Чтобы найти ширину прямоугольника, надо его площадь……………………………………………Чтобы найти длину прямоугольника, надо …………………………………………………………….
Чтобы найти на сколько одно число больше или меньше другого, надо………………………….……………………………………………………………………………………………………………..Чтобы найти во сколько раз одно число больше или меньше другого, надо ……………………….…………………………………………………………………………………………………………………. В выражении без скобок, содержащем только сложение и вычитание или умножение и деление, действия выполняются ………………… ……………………………………………………………. В выражениях, содержащих скобки, сначала выполняются все действия ………………………..…………………………………………………………………………………………………………………………………………………………………………………………………………………………………….. Периметр фигуры – это ………………………………………………………………………………… Периметр прямоугольника равен ……………………………………………………………………… Периметр квадрата равен …………………………………………………………………………………………………. Полупериметр прямоугольника – это ………………………………………………………………….. Чтобы найти сторону квадрата, надо значение его периметра………………………………………… Чтобы найти площадь прямоугольника, надо …………………………………………………………… Чтобы найти ширину прямоугольника, надо его площадь……………………………………………Чтобы найти длину прямоугольника, надо …………………………………………………………….
Чтобы найти неизвестное слагаемое, надо из суммы вычесть другое слагаемое.
Результат умножения двух и более множителей называется произведение.
Чтобы найти делимое, надо делитель умножить на частное.
Результат вычитания чисел называется разность
Результат сложения двух и более слагаемых называется сумма.
Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
Результат деления чисел называется частным.
Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
Чтобы найти делитель, надо делимое разделить на частное.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
Чтобы найти на сколько одно число больше или меньше другого, надоиз большего числа вычесть меньшее.
……………………………………………………………………………………………………………..
Чтобы найти во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.
………………………………………………………………………………………………………………….
В выражении без
скобок, содержащем только сложение и вычитание или умножение и деление,
действия выполняются по порядку. ………………… …………………………………………………………….
………………… …………………………………………………………….
В выражениях, содержащих скобки, сначала выполняются все действия в скобках.………………………..
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Периметр фигуры – это сумма длин всех сторон.
Периметр прямоугольника равен сумме двух сторон, умноженной на 2. Р = 2* (а+в) ………………………………………………………………………
Периметр квадрата равен длина стороны, умноженная на 4………………………………………………………………………………………………….
Полупериметр прямоугольника – это длина двух сторон…………………………………………………………………..
Чтобы найти сторону квадрата, надо значение его периметра разделить на4………………………………………
Чтобы найти площадь прямоугольника, надо значение длины умножить на значение ширины.
Чтобы найти ширину прямоугольника, надо его площадь разделить на длину.……………………………………………
Чтобы найти длину прямоугольника, надо его площадь разделить на ширину.…………………………………………………………….
Как написать сумму разрядных слагаемых.
 Сумма разрядных слагаемых натурального числа
Сумма разрядных слагаемых натурального числаУровень владения приемами устных и письменных вычислений напрямую зависит от усвоения детьми вопросов нумерации чисел. На изучение указанной темы в каждом классе начальной школы отводится определенное количество часов. Как показывает практика, для отработки навыков не всегда бывает достаточно того времени, которое предусмотрено программой.
Понимая всю важность вопроса, опытный учитель обязательно будет включать в каждый урок упражнения, связанные с нумерацией чисел. Кроме того, он учтет виды этих заданий и последовательность их предъявления ученикам.
Требования программы
Для понимания того, к чему необходимо стремиться самому педагогу и его воспитанникам, первый должен четко знать требования, которые выдвигает программа по математике в целом и в вопросах нумерации в частности.
- Ученик должен уметь образовать любые числа (понимать, как это делается) и называть их — требование, которое относится к устной нумерации.

- Изучая письменную нумерацию, дети должны научиться не только записывать числа, но и сравнивать их. При этом они опираются на знание поместного значения цифры в записи числа.
- С понятиями «разряд», «разрядная единица», «разрядное слагаемое» дети знакомятся во втором классе. Начиная с этого же времени термины вводятся в активный словарь школьников. Но учитель употреблял их на уроках математики еще в первом классе, до изучения понятий.
- Знать названия разрядов, записывать число в виде суммы разрядных слагаемых, использовать на практике такие единицы счета, как десяток, сотня, тысяча, воспроизводить последовательность любого отрезка натурального ряда чисел — это тоже требования программы к знаниям учеников начальной школы.
Как использовать задания
Предлагаемые ниже группы заданий помогут учителю в полной мере сформировать умения, которые в итоге приведут к желаемым результатам в области развития вычислительных навыков учеников.
Упражнения могут использоваться на уроках во время повторения пройденного материала, в момент изучения нового.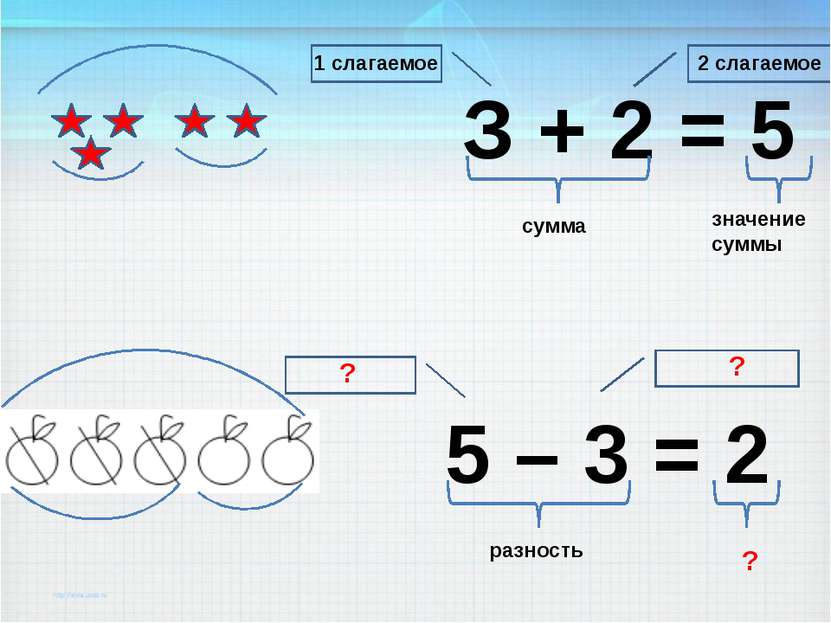 Их можно предлагать для домашних заданий, во внеклассной работе. На материале упражнений учитель может организовать групповые, фронтальные и индивидуальные формы деятельности.
Их можно предлагать для домашних заданий, во внеклассной работе. На материале упражнений учитель может организовать групповые, фронтальные и индивидуальные формы деятельности.
Многое будет зависеть от арсенала приемов и методов, которыми владеет учитель. Но регулярность использования заданий и последовательность отработки навыков — главные условия, которые приведут к успеху.
Образуем числа
Ниже приведены примеры упражнений, направленных на отработку понимания образования чисел. Их необходимое количество будет зависеть от уровня развития учеников класса.
Называем и записываем числа
- Упражнения этого вида включают задания, где требуется назвать числа, представленные геометрической моделью.
- Назовите числа, набрав их на полотне: 967, 473, 285, 64, 3985. Сколько в них содержится единиц каждого разряда?
3. Прочитайте текст и запишите каждое числительное цифрами: на семи … машинах перевезли одну тысячу пятьсот двенадцать … ящиков с помидорами. Сколько понадобится таких машин, чтобы перевезти две тысячи восемьсот восемь … таких же ящиков?
Сколько понадобится таких машин, чтобы перевезти две тысячи восемьсот восемь … таких же ящиков?
4. Запишите числа цифрами. Величины выразите в мелких единицах: 8 сот. 4 ед. = …; 8 м 4 см = …; 4 сот. 9 дес. =…; 4 м 9 дм = …
Читаем и сравниваем числа
1. Прочитайте вслух числа, которые состоят из: 41 дес. 8 ед.; 12 дес.; 8 дес. 8 ед.; 17 дес.
2. Прочитайте числа и подберите к ним соответствующее изображение (на доске в одном столбике записаны различные числа, а в другом — в произвольном порядке изображены модели этих чисел, ученики должны установить их соответствие.)
3. Сравните числа: 416 … 98; 199 … 802; 375 … 474.
4. 35 см … 3 м 6 см; 7 м 9 см … 9 м 3 см
Работаем с разрядными единицами
1. Выразите в разных разрядных единицах: 3 сот. 5 дес. 3 ед. = … сот. … ед. = … дес. … ед.
2. Заполните таблицу:
3. Выпишите числа, где цифра 2 обозначает единицы первого разряда: 92; 502; 299; 263; 623; 872.
4. Запишите трехзначное число, где количество сотен равно трем, а единиц — девяти.
Сумма разрядных слагаемых
Примеры заданий:
- Прочитай записи на доске: 480; 700 + 70 + 7; 408; 108; 400 + 8; 777; 100 + 8; 400 + 80. В первом столбике расположи трехзначные числа, сумма разрядных слагаемых должна находиться во втором столбике. Соедини стрелкой сумму с ее значением.
- Прочитай числа: 515; 84; 307; 781. Замени суммой разрядных слагаемых.
- Запиши пятизначное число, в котором будет три разрядных слагаемых.
- Запиши шестизначное число, содержащее одно разрядное слагаемое.
Изучаем многозначные числа
- Найдите и подчеркните трехзначные числа: 362, 7; 17; 107; 1001; 64; 204; 008.
- Запишите число, у которого 375 единиц первого класса и 79 единиц второго класса. Назовите наибольшее и наименьшее разрядное слагаемое.
- Чем схожи и отличаются друг от друга числа каждой пары: 8 и 708; 7 и 707; 12 и 112?
Применяем новую счетную единицу
- Прочитайте числа и скажите, сколько десятков в каждом из них: 571; 358; 508; 115.

- Сколько сотен содержится в каждом записанном числе?
- Разбейте числа на несколько групп, обосновав свой выбор: 10; 510; 940; 137; 860; 86; 832.
Поместное значение цифры
- Из цифр 3; 5; 6 составьте все возможные варианты трехзначных чисел.
- Прочитайте числа: 6; 16; 260; 600. Какая цифра повторяется в каждом из них? Что она обозначает?
- Найдите сходство и отличие, сравнив числа между собой: 520; 526; 506.
Умеем считать быстро и правильно
В задания этого вида должны включаться упражнения, в которых требуется определенное количество чисел расставить в порядке убывания или возрастания. Можно предложить детям восстановить нарушенный порядок следования чисел, вставить пропущенные, убрать лишние числа.
Находим значения числовых выражений
Используя знания нумерации, ученики без затруднений должны находить значения выражений типа: 800 — 400; 500 — 1; 204 + 40. При этом полезно будет постоянно спрашивать детей, что они заметили, выполняя действие, просить назвать их то или иное разрядное слагаемое, обращать их внимание на положение одной и той же цифры в числе и т. д.
д.
Все упражнения разделены на группы для удобства их использования. Каждая из них может быть дополнена учителем по своему усмотрению. Заданиями такого вида очень богата наука математика. Разрядные слагаемые, которые помогают освоить состав любого многозначного числа, должны занять особое место в подборе заданий.
Если данный подход к изучению нумерации чисел и их разрядного состава будет использоваться учителем на протяжении всех четырех лет обучения в начальной школе, то положительный результат обязательно проявится. Дети будут легко и без ошибок выполнять арифметические вычисления любого уровня сложности.
Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.
Натуральные числа
При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.
Разряды и классы чисел
Разряды
десятков
Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.
Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.
Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.
Классы
Первый — единиц , содержит до 3 знаков:
Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.
Сорок пять состоит из четырёх десятков и пяти простых единиц.
Второй — тысяч , от 4 до 6 знаков:
- 679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.
Эта сумма состоит из следующих разрядных слагаемых:
- шестьсот тысяч;
- семьдесят тысяч;
- девять тысяч;
- восемьсот;
- десять;
- 3 456 = 3000 + 400 +50 +6.
Здесь отсутствуют слагаемые выше четвёртого разряда.
Третий — миллионов , от 7 до 9 цифр:
Это число содержит девять разрядных слагаемых:
- 800 миллионов;
- 80 миллионов;
- 7 миллионов;
- 200 тысяч;
- 10 тысяч;
- 3 тысячи;
- 6 сотен;
- 4 десятка;
- 4 единицы;
В этом числе нет слагаемых выше 7 разряда.
Четвёртый — миллиардов, от 10 до 12 цифр:
Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.
Разрядные слагаемые 4 класса читаются слева направо:
- единицы сотен миллиардов;
- единицы десятков миллиардов;
- единицы миллиардов;
- сотен миллионов;
- десятков миллионов;
- миллионов;
- сотен тысяч;
- десятков тысяч;
- тысяч;
- простые сотни;
- простые десятки;
- простые единицы.
Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:
Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.
Пятый — триллионов, от 13 до 15 знаков.
Читается слева:
Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.
Шестой — квадриллионов, 16-18 цифр.
Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.
Седьмой — квинтиллионов, 19-21 знак.
- 771 642 962 921 398 634 389.
Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.
Восьмой — секстиллионов, 22-24 цифры.
- 842 527 342 458 752 468 359 173
Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.
Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.
Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31 , чем приписывать тридцать один ноль к единице.
Для выполнения некоторых действий над натуральными числами приходится представлять эти натуральные числа в виде суммы разрядных слагаемых или, как еще говорят, раскладывать натуральные числа по разрядам . Не менее важным является обратный процесс — запись натурального числа по сумме разрядных слагаемых.
В этой статье мы очень подробно на примерах разберемся с представлением натуральных чисел в виде суммы разрядных слагаемых, а также научимся записывать натуральное число по его известному разложению по разрядам.
Навигация по странице.
Представление натурального числа в виде суммы разрядных слагаемых.

Как видите, в названии статьи фигурируют слова «сумма» и «слагаемые», поэтому для начала мы рекомендуем хорошо разобраться в информации статьи общее представление о сложении натуральных чисел . Также не помешает повторить материал из раздела разряд, значение разряда натурального числа .
Давайте примем на веру следующие утверждения, которые помогут нам дать определение разрядных слагаемых.
Разрядными слагаемыми могут быть только натуральные числа, записи которых содержат единственную цифру, отличную от цифры 0 . Например, натуральные числа 5 , 10 , 400 , 20 000 и т.п. могут быть разрядными слагаемыми, а числа 14 , 201 , 5 500 , 15 321 и т.п. – не могут.
Количество разрядных слагаемых данного натурального числа должно быть равно количеству цифр в записи данного числа, отличных от цифры 0 . Например, натуральное число 59 можно представить в виде суммы двух разрядных слагаемых, так как в записи этого числа участвуют две цифры (5 и 9 ), отличные от 0 . А сумма разрядных слагаемых натурального числа 44 003 будет состоять из трех слагаемых, так как запись числа содержит три цифры 4 , 4 и 3 , которые отличаются от цифры 0 .
А сумма разрядных слагаемых натурального числа 44 003 будет состоять из трех слагаемых, так как запись числа содержит три цифры 4 , 4 и 3 , которые отличаются от цифры 0 .
Все разрядные слагаемые данного натурального числа в своей записи содержат разное количество знаков.
Сумма разрядных слагаемых данного натурального числа должна быть равна данному числу.
Теперь мы можем дать определение разрядных слагаемых.
Определение.
Разрядные слагаемые данного натурального числа – это такие натуральные числа,
- в записи которых только одна цифра, отличная от цифры 0 ;
- количество которых равно количеству цифр в данном натуральном числе, отличных от цифры 0 ;
- записи которых состоят из разного количества знаков;
- сумма которых равна данному натуральному числу.
Из приведенного определения следует, что однозначные натуральные числа, а также многозначные натуральные числа, записи которых полностью состоят из цифр 0 , за исключением первой цифры слева, не раскладываются в сумму разрядных слагаемых, так как сами являются разрядными слагаемыми некоторых натуральных чисел. Остальные натуральные числа могут быть представлены в виде суммы разрядных слагаемых.
Остальные натуральные числа могут быть представлены в виде суммы разрядных слагаемых.
Осталось разобраться с представлением натуральных чисел в виде суммы разрядных слагаемых.
Для этого нужно вспомнить, что натуральные числа по своей сути связаны с количеством некоторых предметов, при этом в записи числа значения разрядов задают соответствующие количества единиц, десятков, сотен, тысяч, десятков тысяч и так далее. Например, натуральное число 48 отвечает 4 десяткам и 8 единицам, а число 105 070 соответствует 1 сотне тысяч, 5 тысячам и 7 десяткам. Тогда в силу смысла сложения натуральных чисел справедливы следующие равенства 48=40+8 и 105 070=100 000+5 000+70 . Так мы представили натуральные числа 48 и 105 070 в виде суммы разрядных слагаемых.
Рассуждая аналогичным образом, мы можем любое натуральное число разложить по разрядам.
Приведем еще один пример. Представим натуральное число 17 в виде суммы разрядных слагаемых. Число 17 соответствует 1 десятку и 7 единицам, поэтому 17=10+7 . Это и есть разложение числа 17 по разрядам.
Число 17 соответствует 1 десятку и 7 единицам, поэтому 17=10+7 . Это и есть разложение числа 17 по разрядам.
А вот сумма 9+8 не является суммой разрядных слагаемых натурального числа 17 , так как в сумме разрядных слагаемых не может быть двух чисел, записи которых состоят из одинакового количества знаков.
Теперь стало понятно, почему разрядные слагаемые называются именно разрядными. Это связано с тем, что каждое разрядное слагаемое является «представителем» своего разряда данного натурального числа.
Нахождение натурального числа по известной сумме разрядных слагаемых.
Рассмотрим обратную задачу. Будем считать, что нам дана сумма разрядных слагаемых некоторого натурального числа, и нужно найти это число. Для этого можно представить, что каждое из разрядных слагаемых написано на прозрачной пленке, но области с цифрами, отличными от цифры 0, не прозрачны. Чтобы получить искомое натуральное число нужно как бы «наложить» друг на друга все разрядные слагаемые, совмещая их правые края.
К примеру, сумма 300+20+9 представляет собой разложение по разрядам числа 329 , а сумма разрядных слагаемых вида 2 000 000+30 000+3 000+400 соответствует натуральному числу 2 033 400 . То есть, 300+20+9=329 , а 2 000 000+30 000+3 000+400=2 033 400 .
Чтобы найти натуральное число по известной сумме разрядных слагаемых, можно сложить столбиком эти разрядные слагаемые (при необходимости обращайтесь к материалу статьи сложение натуральных чисел столбиком). Разберем решение примера.
Найдем натуральное число, если дана сумма разрядных слагаемых вида 200 000+40 000+50+5 . Записываем числа 200 000 , 40 000 , 50 и 5 так, как того требует способ сложения столбиком:
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу. Получаем
Под горизонтальной линией мы получили искомое натуральное число 240 055 , сумма разрядных слагаемых которого имеет вид 200 000+40 000+50+5 .
В заключении хочется обратить Ваше внимание еще на один момент. Навыки разложения натуральных чисел по разрядам и умение выполнения обратного действия позволяют представлять натуральные число в виде суммы слагаемых, не являющихся разрядными. Например, разложение по разрядам натурального числа 725 имеет следующий вид 725=700+20+5 , а сумму разрядных слагаемых 700+20+5 в силу свойств сложения натуральных чисел можно представить как (700+20)+5=720+5 или 700+(20+5)=700+25 , или (700+5)+20=705+20 .
Возникает логичный вопрос: «Для чего это нужно»? Ответ прост: в некоторых случаях это может упростить вычисления. Приведем пример. Выполним вычитание натуральных чисел 5 677 и 670 . Сначала представим уменьшаемое в виде суммы разрядных слагаемых: 5 677=5 000+600+70+7 . Несложно заметить, что полученная сумма разрядных слагаемых равна сумме (5 000+7)+(600+70)=5 007+670
. Тогда
5 677−670=(5 007+670)−670=
5 007+(670−670)=5 007+0=5 007
.
Список литературы.
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Yandex.RTB R-A-339285-1
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.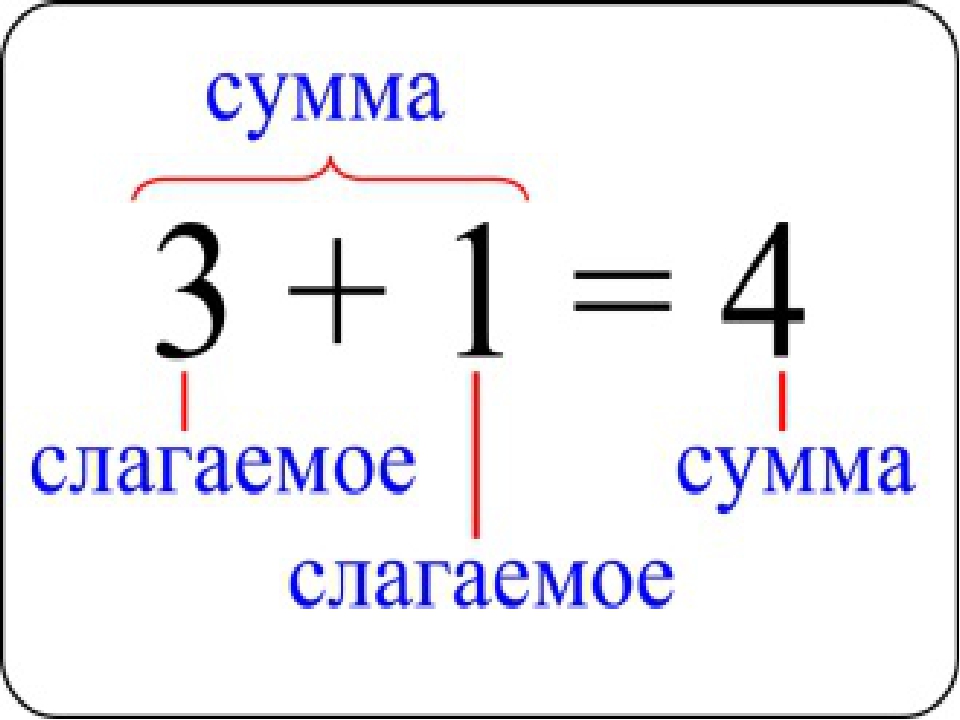
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Определение 1
Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5 , 10 , 400 , 200 относятся к данной категории, а числа 144 , 321 , 5 540 , 16 441 – не относятся.
Количество разрядных слагаемых у представленного числа равняется тому числу, сколько цифр, отличных от нуля, содержится в записи. Если представить число 61 как сумму разрядных слагаемых, так как 6 и 1 отличаются от 0 . Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля.
Определение 2
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Определение 3
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Определение 4
Разрядные слагаемые – это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее. Если вы возьмем, например, число 58 , то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4 тысячам и 4 сотням. Можно представить эти числа в виде равенств – 50 + 8 = 58 и 134 400 = 100 000 + 30 000 + 4 000 + 400 . В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых.
Если вы возьмем, например, число 58 , то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4 тысячам и 4 сотням. Можно представить эти числа в виде равенств – 50 + 8 = 58 и 134 400 = 100 000 + 30 000 + 4 000 + 400 . В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых.
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25 = 20 + 5 . А вот сумма 17 + 8 не является суммой разрядных слагаемых числа 25 , так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.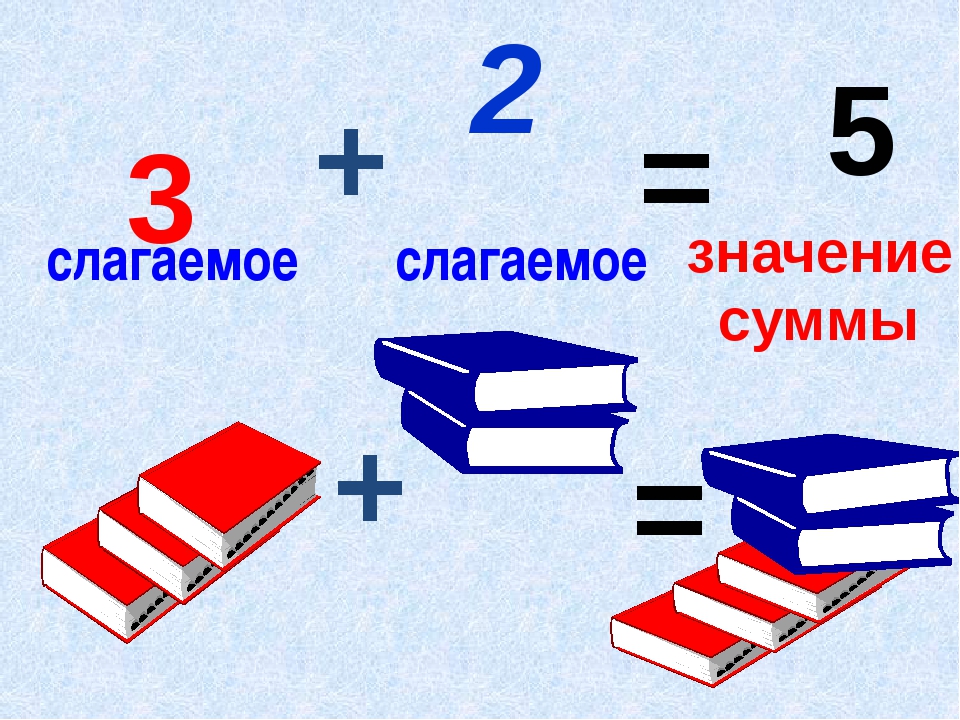
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Например, сумма 200 + 30 + 8 разложено по разрядам числа 238 , а сумма 3 000 000 + 20 000 + 2 000 + 500 соответствует натуральному числу 3 022 500 . Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Пример 1
Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000 + 40 000 + 50 + 5 . Перейдем к решению. Необходимо записать числа 200 000 , 40 000 , 50 и 5 для сложения в столбик:
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Получаем:
Выполнив сложение, мы получим натуральное число 240 055 , сумма разрядных слагаемых которого имеет вид 200 000 + 40 000 + 50 + 5 .
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Пример 2
Разложение по разрядам числа 725 будет представлено как 725 = 700 + 20 + 5 , а сумму разрядных слагаемых 700 + 20 + 5 можно представить как (700 + 20) + 5 = 720 + 5 или 700 + (20 + 5) = 700 + 25 , или (700 + 5) + 20 = 705 + 20 .
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Пример 3
Выполним вычитание чисел 5 677 и 670 . Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677 = 5 000 + 600 + 70 + 7 . Выполнив действие, мы можем сделать вывод, что. сумме ( 5 000 + 7) + (600 + 70) = 5 007 + 670 . Тогда 5 677 − 670 = (5 007 + 670) − 670 = 5 007 + (670 − 670) = 5 007 + 0 = 5 007 .
Выполнив действие, мы можем сделать вывод, что. сумме ( 5 000 + 7) + (600 + 70) = 5 007 + 670 . Тогда 5 677 − 670 = (5 007 + 670) − 670 = 5 007 + (670 − 670) = 5 007 + 0 = 5 007 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
С помощью десяти цифр можно записать любое натуральное число.
От количества знаков (цифр) в числе зависит его название.
Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — 1, наибольшее — 9.
Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — 10, наибольшее — 99.
Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определённое место — позицию.
Разряд — это место (позиция), на котором в записи числа стоит цифра.
Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.
Разряды отсчитываются с конца числа.
Разряд единиц — это самый младший разряд, которым заканчивается любое число.
Цифра 5 — означает 5 единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).
Разряд десятков — это разряд, который стоит перед разрядом единиц.
Цифра 5 — означает 5 десятков, если она стоит на предпоследнем месте (в разряде десятков).
Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра 5 означает 5 сотен, если она стоит на третьем месте от конца числа (в разряде сотен).
Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 (ноль).
Пример. В числе 807 содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа .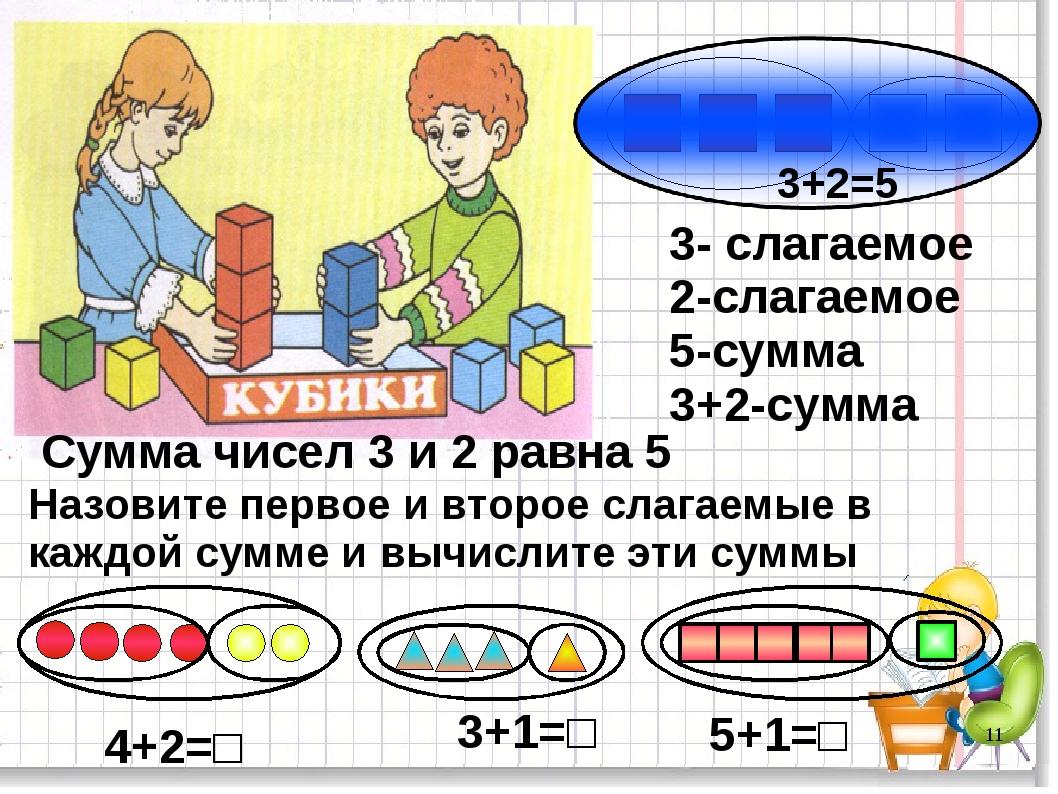
807 = 8 сотен 0 десятков 7 единиц
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.
Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.
Классы и разряды
В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.
Класс единиц или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен .
www.mamapapa-arh.ru
Разрядные слагаемые числа
Сумма разрядных слагаемых
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Как это делается, видно из следующего примера: число 999 состоит из 9 сотен, 9 десятков и 9 единиц, поэтому:
999 = 9 сотен + 9 десятков + 9 единиц = 900 + 90 + 9
Числа 900, 90 и 9 – разрядные слагаемые. Разрядное слагаемое – это просто количество единиц в данном разряде.
Разрядное слагаемое – это просто количество единиц в данном разряде.
Сумму разрядных слагаемых также можно записать следующим образом:
999 = 9 · 100 + 9 · 10 + 9 · 1
Числа, на которые выполняется умножение (1, 10, 100, 1000 и т. д.), называются разрядными единицами . Так, 1 – это единица разряда единиц, 10 – единица разряда десятков, 100 – единица разряда сотен и т. д. Числа, которые умножаются на разрядные единицы выражают количество разрядных единиц .
Запись любого числа в виде:
12 = 1 · 10 + 2 · 1 или 12 = 10 + 2
называется разложением числа на разрядные слагаемые (или суммой разрядных слагаемых ).
3278 = 3 · 1000 + 2 · 100 + 7 · 10 + 8 · 1 = 3000 + 200 + 70 + 8
5031 = 5 · 1000 + 0 · 100 + 3 · 10 + 1 · 1 = 5000 + 30 + 1
3700 = 3 · 1000 + 7 · 100 + 0 · 10 + 0 · 1 = 3000 + 700
Калькулятор разложения числа на разрядные слагаемые
Представить число в виде суммы разрядных слагаемых, вам поможет данный калькулятор. Просто введите нужное число и нажмите кнопку Разложить.
Просто введите нужное число и нажмите кнопку Разложить.
Разрядные слагаемые в математике
Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.
Натуральные числа
При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са?мого большого просто не существует.
Разряды и классы чисел
Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.
Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.
Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.
Первый — единиц , содержит до 3 знаков:
Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.
Сорок пять состоит из четырёх десятков и пяти простых единиц.
Второй — тысяч , от 4 до 6 знаков:
- 679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.
Эта сумма состоит из следующих разрядных слагаемых:
- шестьсот тысяч;
- семьдесят тысяч;
- девять тысяч;
- восемьсот;
- десять;
- 3 456 = 3000 + 400 +50 +6.
Здесь отсутствуют слагаемые выше четвёртого разряда.
Третий — миллионов , от 7 до 9 цифр:
Это число содержит девять разрядных слагаемых:
- 800 миллионов;
- 80 миллионов;
- 7 миллионов;
- 200 тысяч;
- 10 тысяч;
- 3 тысячи;
- 6 сотен;
- 4 десятка;
- 4 единицы;
В этом числе нет слагаемых выше 7 разряда.
Четвёртый — миллиардов, от 10 до 12 цифр:
Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.
Разрядные слагаемые 4 класса читаются слева направо:
- единицы сотен миллиардов;
- единицы десятков миллиардов;
- единицы миллиардов;
- сотен миллионов;
- десятков миллионов;
- миллионов;
- сотен тысяч;
- десятков тысяч;
- тысяч;
- простые сотни;
- простые десятки;
- простые единицы.
Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:
Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого? третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.
Пятый — триллионов, от 13 до 15 знаков.
Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.
Шестой — квадриллионов, 16-18 цифр.
Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.
Седьмой — квинтиллионов, 19-21 знак.
- 771 642 962 921 398 634 389.
Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.
Восьмой — секстиллионов, 22-24 цифры.
- 842 527 342 458 752 468 359 173
Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.
Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.
Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31 , чем приписывать тридцать один ноль к единице.
obrazovanie.guru
Что такое разрядные слагаемые
Ответы и объяснения
Например: 5679=5000+600+70+9
Т. е. кол-во единиц в разряде
- Комментарии (1)
- Отметить нарушение
сумма разрядных слагаемых числа 526 это 500+20+6
«сумма разрядных слагаемых» — это представление дву (или более) значного числа в виде суммы его разрядов.
Разрядные слагаемые — это сложение чисел с разной разрядностью Например число 17.890 разделим на разрядные слагаемые: 17.890=10.000+7.000+800+90+0
Правило умножения любого числа на ноль
Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!» , – но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Кто в итоге прав
Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй. Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:
У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!
Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Это интересно: Как найти разность чисел в математике?
Что такое умножение
Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:
- 25?3 = 75
- 25 + 25 + 25 = 75
- 25?3 = 25 + 25 + 25
Из этого уравнения следует вывод, что умножение — это упрощённое сложение .
Что такое ноль
Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Можно ли умножать на пустоту
Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.
Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:
- Если съесть по два яблока пять раз, то съедено 2?5 = 2+2+2+2+2 = 10 яблок
- Если их съесть по два трижды, то съедено 2?3 = 2+2+2 = 6 яблок
- Если съесть по два яблока ноль раз, то не будет съедено ничего — 2?0 = 0?2 = 0+0 = 0
Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Из всего вышеперечисленного вытекает и другое важное правило:
На ноль делить нельзя!
Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль – это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.
Расскажу тебе позволь,
Чтобы не делил на 0!
Режь 1 как хочешь, вдоль,
Только не дели на 0!
obrazovanie.guru
- Парусные суда Виды парусных судов В зависимости от носимого парусного вооружения (прямое, косое, смешанное) и количества мачт парусные суда носят следующие названия (рис. 44): суда с прямым парусным вооружением — корабль, бриг, с косым парусным вооружением: одномачтовые — шлюп, тендер; полутора-мачтовые -кеч, иол; […]
- Курс уголовного права.
 Общая часть. Том 1. Учение о преступлении
См. Курс уголовного права. Общая часть: Том 1, Том 2, Особенная часть: Том 3, Том 4, Том 5
Глава I. Понятие, предмет, метод, система, задачи уголовного права
_ 1. Предмет и понятие уголовного права
_ 2. Методы уголовного права
_ 3. Задачи […]
Общая часть. Том 1. Учение о преступлении
См. Курс уголовного права. Общая часть: Том 1, Том 2, Особенная часть: Том 3, Том 4, Том 5
Глава I. Понятие, предмет, метод, система, задачи уголовного права
_ 1. Предмет и понятие уголовного права
_ 2. Методы уголовного права
_ 3. Задачи […] - Закон муна Законы Ману — древнеиндийский сборник предписаний религиозного, морально-нравственного и общественного долга (дхармы), называемый также «закон ариев» или «кодекс чести ариев». Манавадхармашастра — одна из двадцати дхармашастр. Здесь представлены избранные фрагменты (перевод Георгия Федоровича […]
- Основные идеи и понятия, необходимые для организации волонтерской (добровольческой) деятельности. 1.Общие подходы к организации волонтерской (добровольческой) деятельности. 1.1.Основные идеи и понятия, необходимые для организации волонтерской (добровольческой) деятельности. 1.2. Законодательные основы волонтерской […]
- Кашин адвокат
адвокатов, включенных в реестр адвокатов Тверской области
Филиал № 1 ТОКА (г.
 Тверь, ул. Советская, 51; т.т.33-20-55;32-07-47;33-20-63) Заведующий филиалом – Стрелков Анатолий Владимирович) (д.т.42-61-44)
1. Дуксова Мария Ивановна – 15.01.1925 г.р. 2. Дунаевский Владимир Евгеньевич –25.11.1953 г.р. […] Антипин вВ адвокат
Вся представленная информация носит ознакомительный характер и не является публичной офертой, определяемой положениями статьи 437 Гражданского кодекса РФ. Представленная информация может утратить актуальность в связи с вносимыми изменениями.
Список адвокатов, оказывающих бесплатную юридическую […]
Тверь, ул. Советская, 51; т.т.33-20-55;32-07-47;33-20-63) Заведующий филиалом – Стрелков Анатолий Владимирович) (д.т.42-61-44)
1. Дуксова Мария Ивановна – 15.01.1925 г.р. 2. Дунаевский Владимир Евгеньевич –25.11.1953 г.р. […] Антипин вВ адвокат
Вся представленная информация носит ознакомительный характер и не является публичной офертой, определяемой положениями статьи 437 Гражданского кодекса РФ. Представленная информация может утратить актуальность в связи с вносимыми изменениями.
Список адвокатов, оказывающих бесплатную юридическую […]
Рекомендуем также
Сумма первых n членов арифметической последовательности
Предположим, что последовательность номеров арифметика (то есть он увеличивается или уменьшается на постоянную величину с каждым членом), и вы хотите найти сумму первых п термины.
Обозначим эту частичную сумму через S п . потом
S
п
знак равно
п
(
а
1
+
а
п
)
2
,
где
п
это количество терминов,
а
1
это первый член и
а
п
это последний срок.
Сумма первых п членов арифметической последовательности называется арифметический ряд .
Пример 1:
Найдите сумму первых 20 члены арифметического ряда, если а 1 знак равно 5 и а 20 знак равно 62 .
S 20 знак равно 20 ( 5 + 62 ) 2 S 20 знак равно 670
Пример 2:
Найдите сумму первых
40
термины арифметики последовательность
2
,
5
,
8
,
11
,
⋯
.
Сначала найдите 40 th срок:
а 40 знак равно а 1 + ( п — 1 ) d знак равно 2 + 39 ( 3 ) знак равно 119
Затем найдите сумму:
S п знак равно п ( а 1 + а п ) 2 S 40 знак равно 40 ( 2 + 119 ) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ k знак равно 1 50 ( 3 k + 2 )
Первая находка а 1 и а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 50 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
S k знак равно k ( а 1 + а k ) 2 S 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Смотрите также: сигма-обозначение ряда и n-й член арифметической последовательности
Сумма первых n членов арифметического ряда
Если
серии
является
арифметика
сумма первых
п
термины, обозначенные
S
п
, есть способы найти его сумму без фактического добавления всех членов.
Чтобы найти сумму первых
п
члены арифметического ряда используют формулу,
п
члены арифметической последовательности используют формулу,
S
п
знак равно
п
(
а
1
+
а
п
)
2
,
где
п
это количество терминов,
а
1
это первый член и
а
п
это последний срок.
Сериал 3 + 6 + 9 + 12 + ⋯ + 30 можно выразить как сигма-обозначение ∑ п знак равно 1 10 3 п . Это выражение читается как сумма 3 п в качестве п идет от 1 к 10
Пример 1:
Найдите сумму первых
20
члены арифметического ряда, если
а
1
знак равно
5
и
а
20
знак равно
62
.
S 20 знак равно 20 ( 5 + 62 ) 2 S 20 знак равно 670
Пример 2:
Найдите сумму первых
40
члены арифметической последовательности
2
,
5
,
8
,
11
,
14
,
⋯
Сначала найдите 40 th срок:
а 40 знак равно а 1 + ( п — 1 ) d знак равно 2 + 39 ( 3 ) знак равно 119
Затем найдите сумму:
S п знак равно п ( а 1 + а п ) 2 S 40 знак равно 40 ( 2 + 119 ) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ k знак равно 1 50 ( 3 k + 2 )
Первая находка а 1 и а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 20 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
S k знак равно k ( а 1 + а k ) 2 S 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Арифметических последовательностей и серии
Арифметические последовательности
Арифметическая последовательность — последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d . , или арифметическая прогрессия. Используется при обращении к арифметической последовательности., представляет собой последовательность чисел, где каждое последующее число является суммой предыдущего числа и некоторой константы d .
, или арифметическая прогрессия. Используется при обращении к арифметической последовательности., представляет собой последовательность чисел, где каждое последующее число является суммой предыдущего числа и некоторой константы d .
an = an − 1 + d Арифметическая последовательность
И поскольку an − an − 1 = d, константа d называется общей разностью Константа d , которая получается вычитанием любых двух последовательных членов арифметической последовательности; an − an − 1 = d .. Например, последовательность положительных нечетных целых чисел является арифметической последовательностью,
1,3,5,7,9,…
Здесь a1 = 1, а разница между любыми двумя последовательными членами равна 2.Мы можем построить общий член an = an − 1 + 2, где,
a1 = 1a2 = a1 + 2 = 1 + 2 = 3a3 = a2 + 2 = 3 + 2 = 5a4 = a3 + 2 = 5 + 2 = 7a5 = a4 + 2 = 7 + 2 = 9 ⋮
В общем, учитывая первый член a1 арифметической последовательности и его общую разность d , мы можем записать следующее:
a2 = a1 + da3 = a2 + d = (a1 + d) + d = a1 + 2da4 = a3 + d = (a1 + 2d) + d = a1 + 3da5 = a4 + d = (a1 + 3d) + d = a1 + 4d ⋮
Отсюда мы видим, что любую арифметическую последовательность можно записать в терминах ее первого элемента, общей разницы и индекса следующим образом:
an = a1 + (n − 1) d Арифметическая последовательность
Фактически, любой общий член, линейный по формуле n , определяет арифметическую последовательность.
Пример 1
Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 -го члена : 7,10,13,16,19,…
Решение:
Начните с поиска общей разницы,
d = 10-7 = 3
Обратите внимание, что разница между любыми двумя последовательными членами равна 3. Последовательность действительно представляет собой арифметическую прогрессию, где a1 = 7 и d = 3.
an = a1 + (n − 1) d = 7 + (n − 1) ⋅3 = 7 + 3n − 3 = 3n + 4
Следовательно, мы можем записать общий член an = 3n + 4. Уделите минуту, чтобы убедиться, что это уравнение описывает заданную последовательность. Используйте это уравнение, чтобы найти член 100 th :
а100 = 3 (100) + 4 = 304
Ответ: an = 3n + 4; а100 = 304
Общая разница арифметической последовательности может быть отрицательной.
Пример 2
Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 75 -го члена: 6,4,2,0, −2,…
Решение:
Начните с поиска общей разницы,
d = 4−6 = −2
Затем найдите формулу для общего члена, здесь a1 = 6 и d = −2.
an = a1 + (n − 1) d = 6 + (n − 1) ⋅ (−2) = 6−2n + 2 = 8−2n
Следовательно, an = 8−2n и член 75 th можно рассчитать следующим образом:
a75 = 8−2 (75) = 8−150 = −142
Ответ: an = 8−2n; а100 = −142
Термины между данными членами арифметической последовательности называются средними арифметическими. Термины между данными членами арифметической последовательности ..
Пример 3
Найдите все члены арифметической последовательности между a1 = −8 и a7 = 10.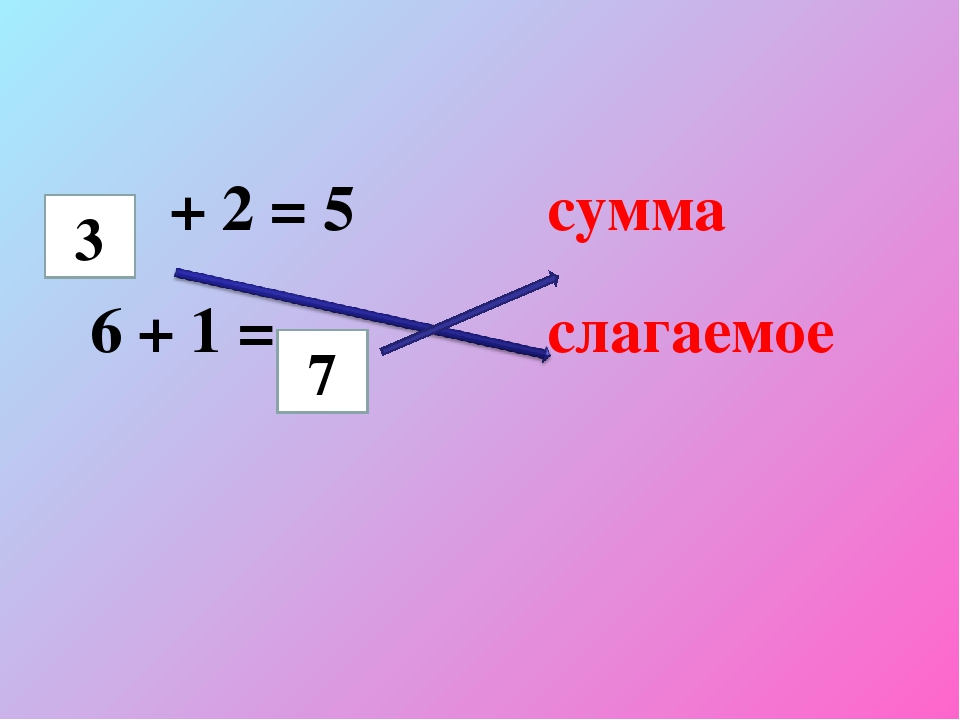 Другими словами, найдите все средние арифметические между 1 и 7 членами.
Другими словами, найдите все средние арифметические между 1 и 7 членами.
Решение:
Начните с поиска общей разницы d . В данном случае нам даны первый и седьмой член:
an = a1 + (n − 1) d Используйте n = 7. a7 = a1 + (7−1) da7 = a1 + 6d
Подставляем a1 = −8 и a7 = 10 в приведенное выше уравнение, а затем решаем общую разность d .
10 = −8 + 6d18 = 6d3 = d
Затем используйте первый член a1 = −8 и общую разность d = 3, чтобы найти уравнение для n -го члена последовательности.
an = −8 + (n − 1) ⋅3 = −8 + 3n − 3 = −11 + 3n
При an = 3n − 11, где n — положительное целое число, найдите пропущенные члены.
a1 = 3 (1) −11 = 3−11 = −8a2 = 3 (2) −11 = 6−11 = −5a3 = 3 (3) −11 = 9−11 = −2a4 = 3 (4) — 11 = 12−11 = 1a5 = 3 (5) −11 = 15−11 = 4a6 = 3 (6) −11 = 18−11 = 7} среднее арифметическое a7 = 3 (7) −11 = 21−11 = 10
Ответ: −5, −2, 1, 4, 7
В некоторых случаях первый член арифметической последовательности может не указываться.
Пример 4
Найдите общий член арифметической последовательности, где a3 = −1 и a10 = 48.
Решение:
Чтобы определить формулу для общего члена, нам нужны a1 и d. Линейная система с этими переменными может быть сформирована с использованием данной информации и an = a1 + (n − 1) d:
{a3 = a1 + (3−1) da10 = a1 + (10−1) d⇒ {−1 = a1 + 2d48 = a1 + 9d Используйте a3 = −1. Используйте a10 = 48.
Исключите a1, умножив первое уравнение на -1, и прибавьте результат ко второму уравнению.
{−1 = a1 + 2d48 = a1 + 9d ⇒ × (−1) + {1 = −a1−2d48 = a1 + 9d¯ 49 = 7d7 = d
Подставляем d = 7 в −1 = a1 + 2d, чтобы найти a1.
−1 = a1 + 2 (7) −1 = a1 + 14−15 = a1
Затем используйте первый член a1 = −15 и общую разность d = 7, чтобы найти формулу для общего члена.
an = a1 + (n − 1) d = −15 + (n − 1) ⋅7 = −15 + 7n − 7 = −22 + 7n
Ответ: an = 7n − 22
Попробуй! Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 -го члена : 32,2,52,3,72,…
Ответ: an = 12n + 1; а100 = 51
Арифметические серии
Арифметический ряд Сумма членов арифметической последовательности. представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
S5 = Σn = 15 (2n − 1) = [2 (1) −1] + [2 (2) −1] + [2 (3) −1] + [2 (4) −1] + [2 (5) −1] = 1 + 3 + 5 + 7 + 9 = 25
Добавлением 5 положительных нечетных целых чисел, как мы сделали выше, можно управлять. Однако рассмотрите возможность добавления первых 100 положительных нечетных целых чисел. Это было бы очень утомительно. Поэтому затем мы разработаем формулу, которая может использоваться для вычисления суммы первых n членов, обозначенных Sn, любой арифметической последовательности.В целом
Sn = a1 + (a1 + d) + (a1 + 2d) +… + an
Записывая эту серию в обратном порядке, мы имеем,
Sn = an + (an − d) + (an − 2d) +… + a1
И сложив эти два уравнения вместе, члены, включающие d , прибавляют к нулю, и мы получаем n множителей a1 + an:
2Sn = (a1 + an) + (a1 + an) +… + (an + a1) 2Sn = n (a1 + an)
Разделив обе стороны на 2, мы получим формулу для n -й частичной суммы арифметической последовательности Сумма первых n членов арифметической последовательности, заданной формулой: Sn = n (a1 + an) 2. :
:
Sn = n (a1 + an) 2
Используйте эту формулу для вычисления суммы первых 100 членов последовательности, определенной как an = 2n − 1. Здесь a1 = 1 и a100 = 199.
S100 = 100 (a1 + a100) 2 = 100 (1 + 199) 2 = 10 000
Пример 5
Найдите сумму первых 50 членов заданной последовательности: 4, 9, 14, 19, 24,…
Решение:
Определите, есть ли общее различие между данными терминами.
d = 9−4 = 5
Обратите внимание, что разница между любыми двумя последовательными членами равна 5. Последовательность действительно является арифметической прогрессией, и мы можем написать
an = a1 + (n − 1) d = 4 + (n − 1) ⋅5 = 4 + 5n − 5 = 5n − 1
Следовательно, общий член an = 5n − 1. Чтобы вычислить частичную сумму 50 -й этой последовательности, нам нужны 1 -е и 50 -е члены:
а1 = 4а50 = 5 (50) -1 = 249
Затем используйте формулу, чтобы определить частичную сумму 50 -й заданной арифметической последовательности.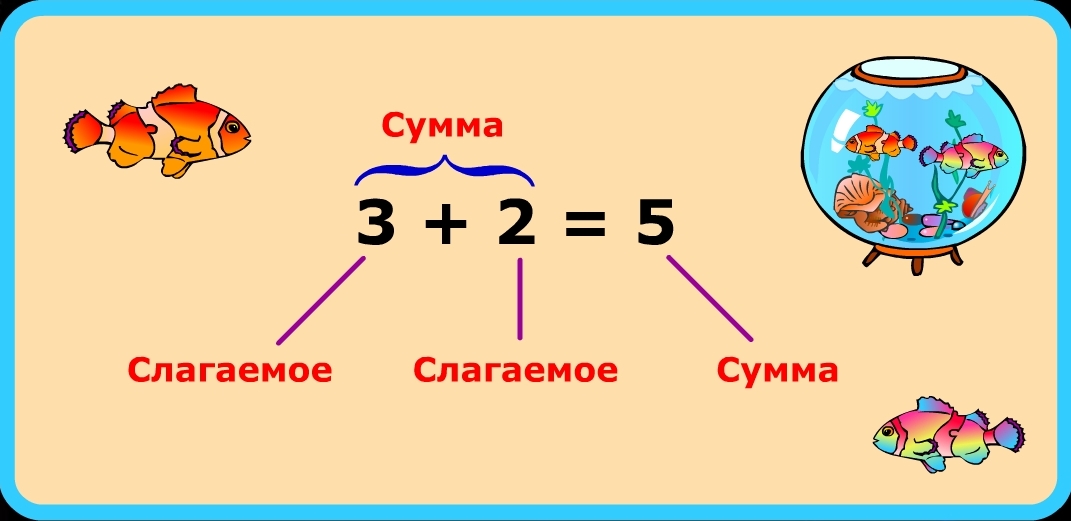
Sn = n (a1 + an) 2S50 = 50. (A1 + a50) 2 = 50 (4 + 249) 2 = 25 (253) = 6,325
Ответ: S50 = 6,325
Пример 6
Вычислить: Σn = 135 (10−4n).
Решение:
В этом случае нам предлагается найти сумму первых 35 членов арифметической последовательности с общим членом an = 10−4n. Используйте это, чтобы определить 1 -й и 35 -й член.
a1 = 10−4 (1) = 6a35 = 10−4 (35) = — 130
Затем используйте формулу для определения частичной суммы 35 -й .
Sn = n (a1 + an) 2S35 = 35⋅ (a1 + a35) 2 = 35 [6 + (- 130)] 2 = 35 (−124) 2 = −2,170
Ответ: −2,170
Пример 7
Первый ряд сидений в амфитеатре под открытым небом содержит 26 сидячих мест, второй ряд — 28 сидений, третий ряд — 30 сидячих мест и так далее. Если рядов 18, какова общая вместимость театра?
Если рядов 18, какова общая вместимость театра?
Рисунок 9.2
Римский театр (Википедия)
Решение:
Начните с поиска формулы, которая дает количество мест в любом ряду.Здесь количество мест в каждом ряду образует последовательность:
26,28,30,…
Обратите внимание, что разница между любыми двумя последовательными членами равна 2. Последовательность представляет собой арифметическую прогрессию, где a1 = 26 и d = 2.
an = a1 + (n − 1) d = 26 + (n − 1) ⋅2 = 26 + 2n − 2 = 2n + 24
Таким образом, количество мест в каждом ряду равно an = 2n + 24. Чтобы рассчитать общую вместимость 18 рядов, нам нужно вычислить частичную сумму 18 th .Для этого нам понадобятся 1 st и 18 th термины:
а1 = 26а18 = 2 (18) + 24 = 60
Используйте это, чтобы вычислить частичную сумму 18 th следующим образом:
Sn = n (a1 + an) 2S18 = 18⋅ (a1 + a18) 2 = 18 (26 + 60) 2 = 9 (86) = 774
Ответ: Всего 774 места.
Попробуй! Найдите сумму первых 60 членов заданной последовательности: 5, 0, −5, −10, −15,…
Ответ: S60 = −8,550
Основные выводы
- Арифметическая последовательность — это последовательность, в которой разница d между последовательными членами является постоянной.
- Общий член арифметической последовательности может быть записан в терминах его первого члена a1, общей разности d и индекса n следующим образом: an = a1 + (n − 1) d.
- Арифметический ряд — это сумма членов арифметической последовательности.
- n -я частичная сумма арифметической последовательности может быть вычислена с использованием первого и последнего членов следующим образом: Sn = n (a1 + an) 2.
Тематические упражнения
−3, −7, −11, −15, −19,…
−6, −14, −22, −30, −38,…
−5, −10, −15, −20, −25,…
−13, 23, 53, 83, 113,…
13, 0, −13, −23, −1,…
14, −12, −54, −2, −114,…
0.
 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…4,4, 7,5, 10,6, 13,7, 16,8,…
Найдите положительное нечетное целое число 50 -го .
Найдите положительное четное число 50 -го .
Найдите 40 -й член в последовательности, состоящей из всех остальных положительных нечетных целых чисел: 1, 5, 9, 13,…
Найдите 40 -й член в последовательности, которая состоит из всех остальных положительных четных чисел: 2, 6, 10, 14,…
Какое число представляет собой член 355 в арифметической последовательности −15, −5, 5, 15, 25,…?
Какое число является членом −172 в арифметической последовательности 4, −4, −12, −20, −28,…?
Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1 + 5, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член через a1 и общую разность d .

Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1−9, где a1 = 4 и n> 1, найдите уравнение, которое дает общий член через a1 и общую разность d .
a4 = −2310 и a21 = −252
Часть A: Арифметические последовательности
Запишите первые 5 членов арифметической последовательности, учитывая их первый член и общую разницу. Найдите формулу для его общего члена.
Найдите формулу для его общего члена.
Зная арифметическую последовательность, найдите формулу для общего члена и используйте ее для определения члена 100 -го .
Учитывая члены арифметической последовательности, найдите формулу для общего члена.
Найдите все средние арифметические значения между заданными членами.
∑n = 1160 (3n)
∑n = 1121 (−2n)
∑n = 1250 (4n − 3)
∑n = 1120 (2n + 12)
∑n = 170 (19−8n)
∑n = 1220 (5 − п)
∑n = 160 (52−12n)
∑n = 151 (38n + 14)
∑n = 1120 (1.
 5n − 2,6)
5n − 2,6)∑n = 1175 (-0,2n-1,6)
Найдите сумму первых 200 натуральных чисел.
Найдите сумму первых 400 натуральных чисел.
Сумма первых 50 положительных нечетных целых чисел.

Сумма первых 200 положительных нечетных целых чисел.
Сумма первых 50 положительных четных целых чисел.
Сумма первых 200 положительных четных целых чисел.
Сумма первых k положительных нечетных целых чисел.
Сумма первых k положительных четных чисел.
Первый ряд в малом театре состоит из 8 мест.
 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?Первый ряд сидений в амфитеатре на открытом воздухе содержит 42 сиденья, второй ряд — 44 сиденья, третий ряд — 46 сидений и так далее.Если рядов 22, какова общая вместимость театра?
Если треугольная стопка кирпичей имеет 37 кирпичей в нижнем ряду, 34 кирпича во втором ряду и так далее, с одним кирпичом наверху. Сколько кирпичей в стопке?
В каждом следующем ряду треугольной стопки кирпичей на один кирпич меньше, пока наверху не останется только один кирпич.Сколько рядов в стеке, если всего кирпичей 210?
10-летний контракт о заработной плате предлагает 65 000 долларов в первый год с увеличением на 3200 долларов каждый дополнительный год.
 Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период.Башня с часами ударяет в колокол количество раз, указанное в часах.В час дня он ударяет один раз, в два — дважды и так далее. Сколько раз за день башня с часами бьет в колокол?
Часть B: Арифметическая серия
Вычислите указанную сумму по формуле для общего члена.
Оценить.
Общий член для последовательности положительных нечетных целых чисел задается как an = 2n − 1, а общий член для последовательности положительных четных целых чисел определяется как an = 2n. Найдите следующее.
Является ли последовательность Фибоначчи арифметической последовательностью? Объяснять.
Используйте формулу для n -й частичной суммы арифметической последовательности Sn = n (a1 + an) 2 и формулу для общего члена an = a1 + (n − 1) d, чтобы получить новую формулу для n -я частичная сумма Sn = n2 [2a1 + (n − 1) d].
 При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.Обсудите методы расчета сумм, в которых индекс не начинается с 1. Например, Σn = 1535 (3n + 4) = 1,659.
Известная история повествует о плохом поведении Карла Фридриха Гаусса в школе.В наказание учитель дал ему задание сложить первые 100 целых чисел. Легенда гласит, что молодой Гаусс правильно ответил в считанные секунды. Каков ответ и как вы думаете, он смог так быстро найти сумму?
Часть C: Обсуждение
ответов
5, 8, 11, 14, 17; ан = 3n + 2
15, 10, 5, 0, −5; ан = 20−5н
12, 32, 52, 72, 92; an = n − 12
1, 12, 0, −12, −1; ан = 32−12н
1.
 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2ан = 1.
 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6
7.
 2 — Арифметические последовательности 7.2 — Арифметические последовательности
2 — Арифметические последовательности 7.2 — Арифметические последовательностиАрифметическая последовательность — это последовательность, в которой разница между последовательными сроки постоянны.
Общее различие
Поскольку это различие является общим для всех последовательных пар терминов, оно называется общая разница. Обозначается буквой d. Если разница в последовательных термины не постоянны, то последовательность не арифметическая. Общая разница можно найти, вычитая два последовательных члена последовательности.
Формула для общей разности арифметической последовательности: d = a n + 1 — а п
Общие условия
Арифметическая последовательность — это линейная функция. Вместо y = mx + b пишем a n = dn + c где d — общая разность, а c — константа (не первый член последовательность, однако).
Рекурсивное определение, поскольку каждый термин находится путем добавления общей разницы
к предыдущему члену k + 1 = k + d.
Для любого термина в последовательности мы добавили разницу на один раз меньше, чем номер срока. Например, для первого члена мы не добавили разница вообще (0 раз). Для второго члена мы добавили разницу однажды. Для третьего члена мы добавили разницу в два раза.
Формула для общего члена арифметической последовательности: a n = а 1 + (п-1) г
Частичная сумма арифметической последовательности
Серия — это сумма последовательности.Мы хотим найти частичный номер n th сумма или сумма первых n членов последовательности. Обозначим частичный номер n th . Сумма как S n .
Рассмотрим арифметический ряд S 5 = 2 + 5 + 8 + 11 + 14. Там это простой способ вычислить сумму арифметического ряда.
S 5 = 2 + 5 + 8 + 11 + 14
Ключ в том, чтобы изменить порядок терминов. Сложение коммутативно, поэтому изменение заказ не меняет сумму.
ю.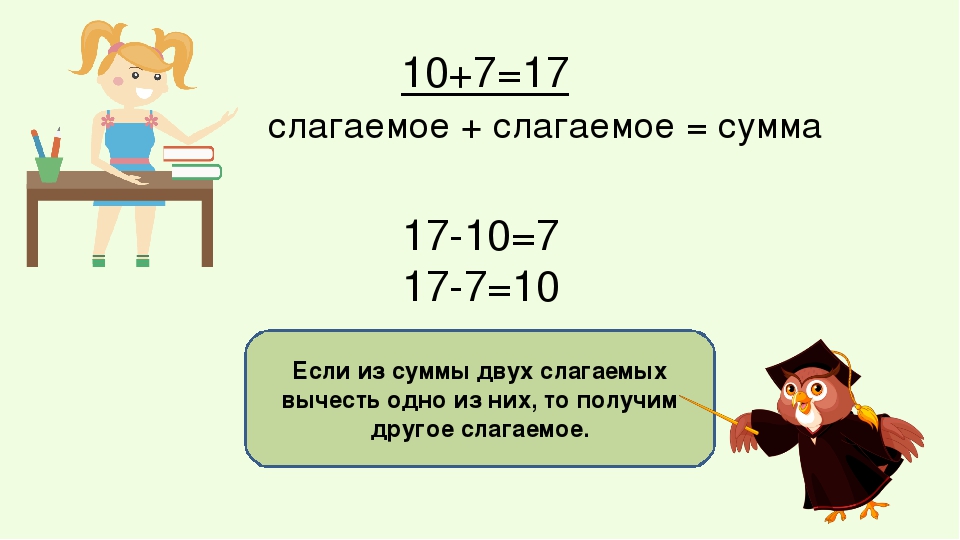 ш. 5 = 14 + 11 + 8 + 5 + 2
ш. 5 = 14 + 11 + 8 + 5 + 2
Теперь сложите эти два уравнения вместе.
2 * S 5 = (2 + 14) + (5 + 11) + (8 + 8) + (11 + 5) + (14 + 2)
Обратите внимание, что каждая из этих сумм в правой части равна 16. Вместо записи 16 (сумма первого и последнего слагаемых) пять раз, мы можем записать это как 5 * 16 или 5 * (2 + 14)
2 * S 5 = 5 * (2 + 14)
Наконец, разделите все на 2, чтобы получить сумму, а не удвоенную сумму
ю.ш. 5 = 5/2 * (2 + 14)
Я специально не упрощал 2 + 14, чтобы вы могли видеть, где числа родом из.Эта сумма будет 5/2 * (16) = 5 (8) = 40.
Теперь, если мы попытаемся выяснить, откуда берутся различные части этой формулы
откуда мы можем сделать предположение о формуле для частичной суммы n th .
5 — потому что было пять членов, n. 16 — это сумма первого и
последние условия, a 1 + a n . 2 потому что мы добавили сумму
дважды и останется 2.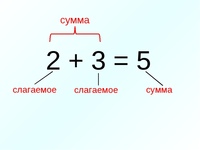 Следовательно, сумма первых n членов арифметического
последовательность: S n = n / 2 * (a 1 + a n )
Следовательно, сумма первых n членов арифметического
последовательность: S n = n / 2 * (a 1 + a n )
Есть еще одна формула, которая иногда используется для частичного n th сумма арифметической последовательности.Он получается подстановкой формулы для общий термин в приведенной выше формуле и упрощение. Предпочтительный метод — найти термин n th , а затем просто вставить этот номер в формулу.
S n = n / 2 * (2a 1 + (n-1) d)
ПримерНайдите сумму от k = 3 до 17 из (3k-2).
Первый член находится заменой k = 3 на 3k-2, чтобы получить 7. Последний член член 3 (17) -2 = 49.Всего 17 — 3 + 1 = 15 терминов. Итак, сумма составляет 15 / 2 * (7 + 49) = 15/2 * 56 = 420.
Обратите внимание, что там 15 терминов. Когда нижний предел суммирования
равно 1, выяснить количество терминов не составляет труда. Тем не мение,
когда нижний предел — любое другое число, это, кажется, вызывает у людей затруднения. Никто не станет спорить, что если перейти от 1 к 10, получится 10 цифр. Тем не мение,
разница между 10 и 1 составляет всего 9. Итак, когда вы находите число
терминов это верхний предел минус нижний предел плюс один.
Никто не станет спорить, что если перейти от 1 к 10, получится 10 цифр. Тем не мение,
разница между 10 и 1 составляет всего 9. Итак, когда вы находите число
терминов это верхний предел минус нижний предел плюс один.
mathschallenge.net
Часто задаваемые вопросы
Есть ли формула для сложения последовательности кубиков?
Изучив первые пять сумм, можно сделать замечательное открытие:
1 3 = 1
1 3 +2 3 = 9
1 3 +2 3 +3 3 = 36
1 3 +2 3 +3 3 +4 3 = 100
1 3 +2 3 +3 3 +4 3 +5 3 = 225
Кажется, что сумма всегда квадратная, но еще более примечательно то, что сумма первых n кубов, 1 3 +2 3 +… + n 3 = ( n ( n +1) / 2) 2 , который является квадратом числа треугольника n th .
Например, 1 3 +2 3 + … + 10 3 = (10 × 11/2) 2 = 55 2 = 3025.
Используя аналогичный метод, использованный для доказательства этой формулы для суммы квадратов, мы докажем этот результат дедуктивно; есть надежда, что это даст некоторое представление о том, как дальше может быть найден ряд сил.
Доказательство
| r 4 — ( r –1) 4 | = | n 4 — ( n –1) 4 + ( n –1) 4 — ( n –2) 4 + … + 3 4 — 2 4 + 2 4 –1 4 + 1 4 –0 4 | |
| = | n 4 |
Но r 4 — ( r –1) 4 = r 4 — ( r 4 –4 r 3 +6 r 2 –4 r +1) = 4 r 3 –6 r 2 +4 r –1.
| ∴ ∑ 4 r 3 –6 r 2 +4 r –1 | = | 4∑ r 3 — 6∑ r 2 + 4∑ r — ∑1 |
| = | 4∑ r 3 -6 n ( n +1) (2 n +1) / 6 + 4 n ( n +1) / 2- n | |
| = | 4∑ r 3 — n ( n +1) (2 n +1) + 2 n ( n +1) — n | |
| = | № 4 . |
| ∴ 4∑ r 3 | = | n 4 + n ( n +1) (2 n +1) — 2 n ( n +1) + n |
| = | n ( n 3 + ( n +1) (2 n +1) — 2 ( n +1) + 1 | |
| = | n ( n 3 + 2 n 2 +3 n +1 — 2 n –2 + 1) | |
| = | n ( n 3 +2 n 2 + n ) | |
| = | n 2 ( n 2 +2 n +1) | |
| = | n 2 ( n +1) 2 | |
| ∴ ∑ r 3 | = | n 2 ( n +1) 2 /4 |
| = | ( n ( n +1) / 2) 2 |
Другими словами, сумма первых n кубов является квадратом суммы первых n натуральных чисел.
Нахождение суммы последовательности целых чисел
Когда в вопросе предлагается сложить большое количество целых чисел, может показаться, что поиск ответа может занять некоторое время. Но GMAT — это умные ярлыки. Вот быстрый метод, который сделает вас счастливыми, если вы будете получать такие вопросы в день тестирования.
Рассмотрим следующий вопрос от наставника Economist GMAT:
Для каждого положительного целого числа n n-й член последовательности представляет собой сумму трех последовательных целых чисел, начинающихся с n.Какова сумма членов с 1 по 99 этой серии?
Правила быстрого нахождения суммы этой последовательности целых чисел
Правило № 1: Сумма последовательности целых чисел — это среднее значение последовательности целых чисел, умноженное на количество членов.
Если это правило звучит знакомо, то это потому, что это просто еще одна версия формулы для нахождения среднего:
- Среднее = Сумма терминов / Количество терминов
Теперь, как определить среднее значение последовательность целых чисел?
Правило № 2: Среднее значение последовательности целых чисел — это среднее значение первого и последнего членов.
Применение правил для нахождения суммы последовательности
Как мы применим эти полезные правила к этому вопросу?
Сначала вычислите среднее значение первого и последнего членов.
- Первый член представляет собой сумму 1, 2 и 3 = 6
- Последний член представляет собой сумму 99, 100 и 101 = 300
- Среднее значение первого и последнего членов = (6 + 300) / 2 = 306/2 = 153
Во-вторых, умножьте среднее значение на количество членов.
- Есть 99 терминов
- Следовательно, ответ на наш вопрос: 153 x 99
Обратите внимание, что быстрый способ вычислить это без калькулятора — это умножить 153 x 100 и вычесть 153.
- 153 x 100 = 15 300
- 15 300 — 153 = 15 147
И это наш окончательный ответ!
Вы можете видеть, как применение простых правил значительно упрощает вопросы, которые кажутся сложными. Ваша задача собрать как можно больше таких правил.
Ваша задача собрать как можно больше таких правил.
Это был образец подробных инструкций, которые Economist GMAT Tutor предлагает по решению задач в разделе GMAT Quant. Чтобы получить полные и интерактивные уроки, практические тесты и поддержку онлайн-преподавателей, подпишитесь на один из самых популярных планов подготовки к GMAT от Economist GMAT Tutor.Пробные версии без обязательств доступны в течение семи дней.
Wolfram | Alpha Примеры: Суммы
Конечные суммы
Вычислить конечное суммирование математического выражения.
Суммируйте неполностью указанную последовательность терминов:
Другие примеры
Бесконечные суммы
Найдите сумму бесконечного числа членов.
Вычислить сумму по всем целым числам:
Вычислить бесконечную сумму (пределы не указаны):
Просуммируйте неполностью заданный бесконечный ряд:
Другие примеры
.


 для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.].- 8-е изд. — М.: Просвещение, 2011. — 112 с.: ил. — (Школа России). — ISBN 978-5-09-023769-7.
для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.].- 8-е изд. — М.: Просвещение, 2011. — 112 с.: ил. — (Школа России). — ISBN 978-5-09-023769-7.

 Общая часть. Том 1. Учение о преступлении
См. Курс уголовного права. Общая часть: Том 1, Том 2, Особенная часть: Том 3, Том 4, Том 5
Глава I. Понятие, предмет, метод, система, задачи уголовного права
_ 1. Предмет и понятие уголовного права
_ 2. Методы уголовного права
_ 3. Задачи […]
Общая часть. Том 1. Учение о преступлении
См. Курс уголовного права. Общая часть: Том 1, Том 2, Особенная часть: Том 3, Том 4, Том 5
Глава I. Понятие, предмет, метод, система, задачи уголовного права
_ 1. Предмет и понятие уголовного права
_ 2. Методы уголовного права
_ 3. Задачи […]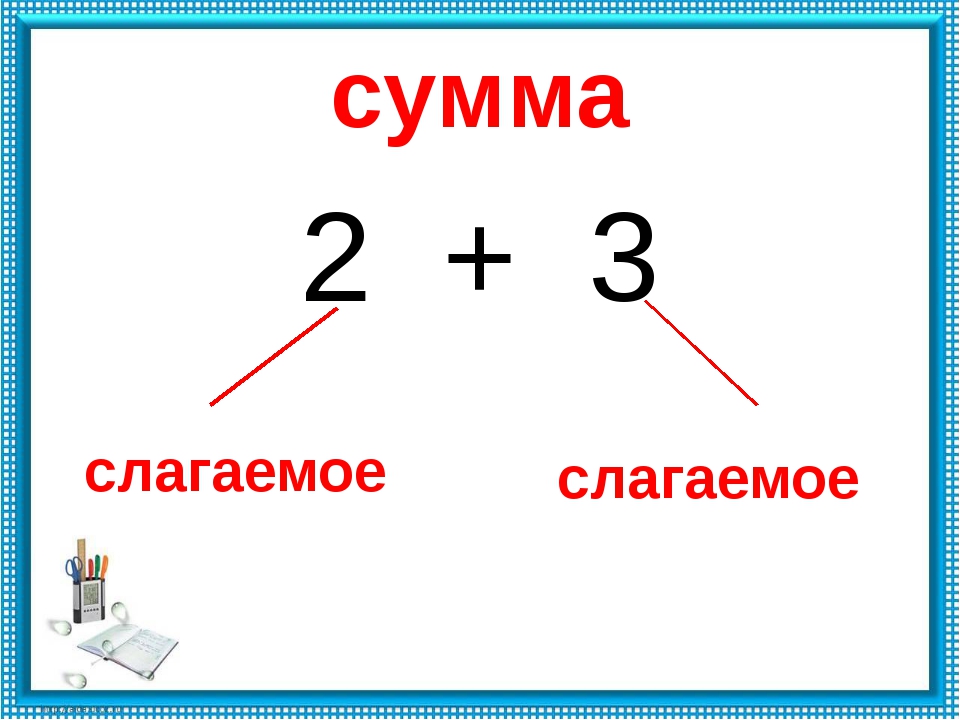 Тверь, ул. Советская, 51; т.т.33-20-55;32-07-47;33-20-63) Заведующий филиалом – Стрелков Анатолий Владимирович) (д.т.42-61-44)
1. Дуксова Мария Ивановна – 15.01.1925 г.р. 2. Дунаевский Владимир Евгеньевич –25.11.1953 г.р. […] Антипин вВ адвокат
Вся представленная информация носит ознакомительный характер и не является публичной офертой, определяемой положениями статьи 437 Гражданского кодекса РФ. Представленная информация может утратить актуальность в связи с вносимыми изменениями.
Список адвокатов, оказывающих бесплатную юридическую […]
Тверь, ул. Советская, 51; т.т.33-20-55;32-07-47;33-20-63) Заведующий филиалом – Стрелков Анатолий Владимирович) (д.т.42-61-44)
1. Дуксова Мария Ивановна – 15.01.1925 г.р. 2. Дунаевский Владимир Евгеньевич –25.11.1953 г.р. […] Антипин вВ адвокат
Вся представленная информация носит ознакомительный характер и не является публичной офертой, определяемой положениями статьи 437 Гражданского кодекса РФ. Представленная информация может утратить актуальность в связи с вносимыми изменениями.
Список адвокатов, оказывающих бесплатную юридическую […] 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…
 5n − 2,6)
5n − 2,6)
 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре? Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период. При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере. 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6