Обведи фигуры по точкам: Плоские геометрические фигуры — Обведи и дорисуй!

Содержание

Плоские геометрические фигуры — Обведи и дорисуй!

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги. Поэтому очень важно начинать обучение малышей с таких развивающих заданий, которые мы собрали для вас на этой странице.

1. Плоские геометрические фигуры — Обведи, дорисуй и раскрась:

В этом развивающем уроке ребенок встретит два задания, с помощью которых он научится рисовать плоские геометрические фигуры: раскрашивание фигур определенным образом и обведение фигур по пунктирной линии, а затем дорисовке отсутствующей части.

В первом задании малыш с помощью пространственного мышления должен расположить (т. е. раскрасить) фигуры таким образом, чтобы каждая из них либо накрывала соседнюю, либо оказывалась под ней. Итак, условие к заданию: квадрат накрыл один угол треугольника, овал оказался на прямоугольнике, а треугольник разместился под кругом. Как вы уже догадались, для того, чтобы получилась такая картина, нужно соприкасающиеся фигуры раскрашивать в разные цвета.
Во втором задании ребенку предстоит обвести пунктирные линии, определить в процессе форму обводимой фигуры и дорисовать самостоятельно ее недостающую часть. После этого фигуры можно раскрасить в произвольные цвета.

Чтобы объяснить ребенку, какие отличия имеют плоские геометрические фигуры и объемные, можете дополнить занятие следующим примером. Из листа обычной бумаги вырежьте квадрат и дайте ребенку, чтобы он оценил его поверхность и объем. Пусть малыш ощутит его в руках, затем положит на стол и посмотрит на фигуру со всех сторон. Скажите ему, что квадрат, который он держит в руках — плоский. После этого возьмите обычный детский кубик и, дав ребенку, скажите, что этот предмет также является квадратом, только теперь он объемный. Дайте ему пощупать кубик, покрутить в руках и посмотреть на него со всех сторон. Не нужно больше ничего говорить и тем более что-то объяснять и разжевывать.

Скачать задание — Плоские геометрические фигуры вы можете во вложениях.

2. Простые геометрические фигуры карандашом — Обведи по точкам

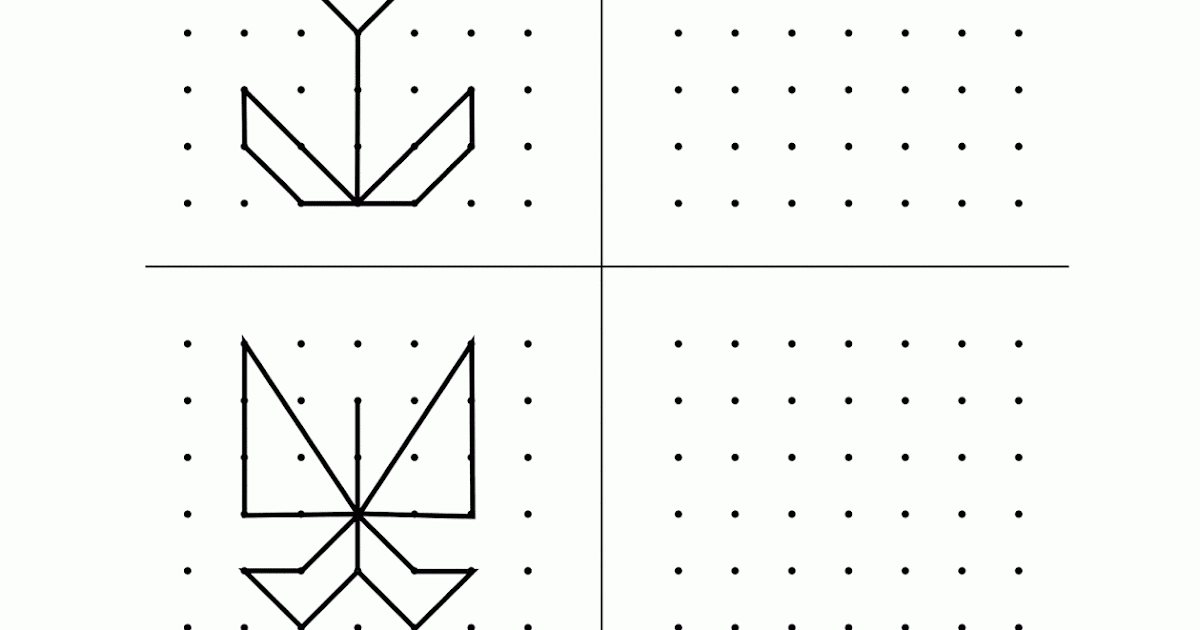
Обводить рисунки по точкам — чрезвычайно интересное занятие для детей. Используя этот детский интерес можно научить их рисовать простые геометрические фигуры, а заодно и потренировать воображение. Ведь в этом задании малыш должен в уме представить, какие точки нужно соединить между собой, чтобы получилась заданная фигура. Данное задание также формирует полезный для школы навык — умение ориентироваться на образец и заданные требования.

Задания необходимо выполнять карандашом, чтобы можно было в процессе работы стереть ластиком ненужные линии. Ведь ребенок будет ошибаться и это абсолютно нормально. Помните, «не ошибается тот, кто ничего не делает».

Вам нужно скачать 2 бланка с простыми геометрическими фигурами. На каждом бланке дается по 3 задания. В 1 и 5 задании нужно нарисовать по образцу неправильные треугольники, во 2 задании — неправильную трапецию, в 3 задании — ромб, в 4 задании — соединить по точкам квадрат, а в 6 задании — четырех лучевую звезду.

Как проводить занятие. Взрослый дает ребенку рассмотреть первое задание и указывая на три вершины треугольника говорит: «Видишь, сначала здесь были точки, которые соединили между собой таким образом, что получился этот рисунок (взрослый указывает на стороны треугольника, но не произносит слов «треугольник», «вершина», «стороны»). А вот здесь (и показывает на точки рядом с треугольником) нарисованы точки, из которых тебе следует выбрать такие, соединив которые получится точно такой рисунок. Но будь внимателен, так как здесь есть лишние точки — их соединять не нужно. Ты сам должен решить, какие точки лишние.»

Затем взрослый предлагает ребенку рассмотреть нарисованные точки и спрашивает у него «Все ли точки одинаковые?» Когда ребенок ответит «Нет», взрослый, подтвердив его ответ, объясняет ребенку условия соединения точек: «Все точки разные. Здесь есть белые точки, черные и с крестиком внутри. Ты должен запомнить правила: одинаковые точки нельзя соединять между собой, нельзя проводить линию от белой точки к белой, от черной — к черной, от точки с крестиком — к точке с крестиком.

То есть соединять между собой можно только разные точки. Запомнил? Теперь можешь приступать к выполнению заданий.»

Скачать задание «Простые геометрические фигуры карандашом — Обведи по точкам» вы можете во вложениях внизу страницы.

3. Дорисуй фигуру по образцу — Геометрия для малышей

Еще одно развивающее занятие по рисованию и запоминанию геометрических фигур — Дорисуй фигуру по образцу. Здесь ребенок должен дорисовать недостающие элементы в каждой фигуре, руководствуясь бланком с готовыми фигурами. Для занятия необходимы: карандаш, ластик, линейка, 4 распечатанных бланка заданий.

Прежде чем приступить к выполнению упражнения, объясните ребенку правила, по которым он должен действовать:

В первом задании (бланки №1 и №2) ребенку сначала нужно внимательно рассмотреть бланк №1 с готовыми геометрическими фигурами. Затем спросите его, какие фигуры из нарисованных ему знакомы. Подскажите ребенку название тех фигур, которые он не сможет назвать. Когда с фигурами станет все предельно ясно — дайте ребенку бланк №2 с недостающими деталями и скажите ему, что на этом листе геометрические фигуры немного испортились. И теперь его задача — исправить их для получения точно такого результата, как на бланке №1.
Во втором задании (бланки №3 и №4) упражнение проводится аналогично предыдущему. Только в отличие от первого задания, здесь ребенку нужно не только дорисовать фигуры, но и дораскрасить, ориентируясь на образец.

Фигуры с прямыми линиями легче дорисовать с помощью линейки. Если ребенок еще не умеет ей пользоваться, то взрослый должен показать ему, как это делать.

Скачать задания «Дорисуй фигуру по образцу» вы можете во вложениях внизу страницы.

Бланк №1 — Готовые фигуры для 1 задания

Бланк №2 — Фигуры с недостающими деталями для 1 задания

Бланк №3 — Готовые фигуры для 2 задания

Бланк №4 — Фигуры с недостающими частями для 2 задания

4.

Упражнение «Найди геометрические фигуры»

Здесь вы можете скачать и распечатать бланк с заданием — Найди геометрические фигуры — для занятий с ребенком или с группой детей. Такие упражнения очень важны для развития логико-математических способностей в процессе обучения (или подготовке к обучению) начальных азов геометрии.

Распечатанный бланк с заданием нужно дать ребенку и попросить его внимательно рассмотреть изображение и найти в нем 1 четырехугольник и 5 треугольников.

Скачать задание «Найди геометрические фигуры» вы можете во вложениях внизу страницы

Чтобы продолжить изучать с ребенком геометрию, можете скачать геометрические фигуры для вырезания из бумаги, распечатать, вырезать и использовать как дополнительный обучающий материал.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Рисунки из геометрических фигур — Задания в картинках и раскраски

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Геометрические фигуры и их названия — Задания в картинках

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.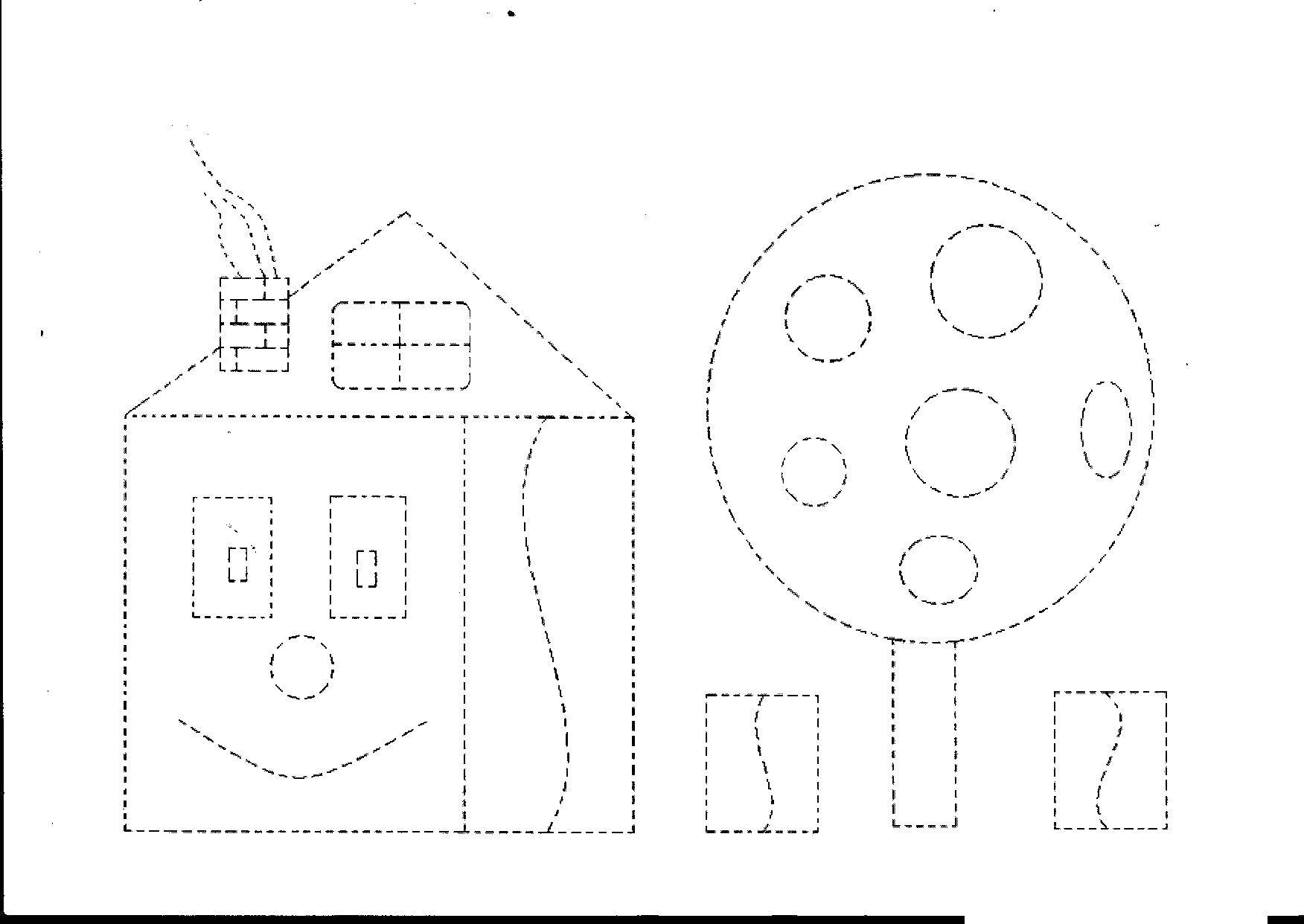

Геометрические фигуры — Раскраска для дошкольников

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Найди формы геометрических фигур в картинках

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга — Задание для детей

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Свойства геометрических фигур для дошкольников

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Счет геометрических фигур — Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

Чертежи геометрических тел — Задание для детей

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Геометрические фигуры из бумаги — Вырезаем и занимаемся

Счет до 5 — Картинки с заданиями для малышей

Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра «Что лишнее? — Геометрические формы»

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Рисуем фигуры по точкам

По теме: методические разработки, презентации и конспекты

данное пособие можно использовать при работе по подготовке руки к письму. развивает мелкую моторику, память, мышление. Картинки взяты с сайта «Дети-сети».

Методика диагностики уровня развития наглядно-действенного мышления детей 4-6 лет.

Задание предназначено для старшего дошкольного возроста. Обведи по точкам. Изучаем буквы и развиваем графомоторные навыки.

Игра задание «Обведи по точкам». С помощью таких игровых заданий происходит развитие у детей целостного в.

обведи по точкам.

Игра направленная на профилактику оптической дизграфии.

Геометрия — одна из важных дисциплин, которую должен изучать каждый ребенок. Чтобы правильно решать задачи, важно знать, что такое шар, круг, квадрат, треугольник, ромб. Сайт https://childdevelop.ru предлагает малышам карточки под названием «Рисуем геометрические фигуры по точкам». Они помогают научиться правильно рисовать квадраты, прямоугольники, трапеции и треугольники, чтобы в будущем было легко усваивать информацию на уроках геометрии.

Ресурс предлагает следующие обводилки для детей по точкам:

копирование геометрических фигур по шести, восьми, десяти, двенадцати точкам;
задания на тренировку зрительно-моторной координации;
рисование треугольника, пятиугольника, шестиугольника;
создание овала, треугольника, квадрата, круга, ромба, прямоугольника на бумаге;
задания «Веселые кубики»;
рисование четырехконечной, пятиконечной звезды;
упражнения на тренировку пространственного воображения.

Преимущества заданий под названием «Рисование геометрических фигур посредством соединения точек»

Карточки «Рисуем по точкам для детей» имеют такие плюсы:

учимся рисовать пунктиром, чтобы получались аккуратные квадраты, треугольники и круги;
задания подходят родителям, которые не знают, как научить чадо строить простые и сложные геометрические фигуры;
малыш становится усидчивым, внимательным;
он получает базовые навыки рисования;
обучение по карточкам «Рисуем фигуры по точкам» проходит легче благодаря тому, что малыш увлечен процессом.

Причины, по которым этот Интернет-ресурс выбирают многие мамы и папы

Все обучающие материалы предоставляются бесплатно. Чтобы скачать урок достаточно предварительно пройти простой процесс регистрации и выбрать понравившуюся красочную карточку. После этого ее нужно скачать и распечатать, чтобы малыш мог рисовать непосредственно на ней.

Изучение нового материала происходит эффективнее, поскольку всем малышам нравится рисовать. Чадо будет долго и увлеченно стараться, чтобы изображение получилось таким же, как и на примере. Уроки «Рисуем геометрические фигуры по точкам» специально были разработаны для дошкольников и школьников для тренировки творческого мышления.

Копирование, тиражирование или распространение информации
сайта «Развитие ребенка» на любых носителях информации и в любом виде запрещено.

Задания и упражнения из раздела «Обводилки» в нескучной форме помогут ребенку подготовить руку к письму. Очень важно тренировать мелкую моторику, умение правильно держать карандаш, способность вписывать фигуры в ограниченное пространство, рисовать точно по линиям, не выходя за контуры. Для выполнения заданий Вам необходим принтер и 20 минут времени каждый день!

Рисование по точкам. Упражнения по развитию графических навыков ребенка Рисуем по точкам, развивая навыки постепенно

Игрушки рано или поздно наскучивают детям, и они начинают искать другие увлекательные для себя занятия. Отличным решением в данном случае может стать наша подборка раскрасок, причем не обычных. Для того чтобы приступить к раскрашиванию ребенку нужно будет предварительно обвести рисунок по контуру. Такие нехитрые с виду игры не только интересны, но и чрезвычайно полезны для детей, они хорошо развивают моторику ручек, усидчивость, внимательность и память. С их помощью ребенок учится находить соответствие между нарисованными предметами и теми, что он видит в реальной жизни.

Обводилки – это прекрасный способ развивать логическое мышление. Угадывая образы на картинке, ребенок может дополнять их собственными идеями, отображая их на рисунке. Кроме того они помогают в развитии творческих способностей. С первого раза малышу будет сложно ровно обвести изображение, но со временем движения карандаша будут четче и увереннее. С такими навыками ребенку будет проще в школе освоить прописи, ведь они созданы по тому же принципу, что и наши раскраски. Сделайте досуг вашего малыша еще более интересным и полезным, скачайте на нашем сайте прекрасный набор раскрасок-обводилок!

Обведи по контуру Утенка

Обведи по контуру Козленка

Обведи по контуру Щенка

Обведи по контуру Лягушку

Обведи по контуру Зайчика

Обведи по контуру Поросенка

Обведи по контуру Червяка

Обведи по контуру Ослика

Обведи по контуру Крота

Обведи по контуру Барашка

Обведи по контуру Лошадку

Обведи по контуру Киску

Обведи по контуру Мышку

Дорогие мамы, за время работы нашей тематической недельки «Геометрические фигуры» обнаружилась распространённая, как оказалось, проблема, волнующая многих мам:

у ребёнка не получается обводить фигуры по контуру,
отказывается выполнять такие задания, как обводка и раскраски,
не любит рисовать, не хочет рисовать карандашами,
не умеет держать ручку-карандаш в руке.

Я подготовила ряд статей, в которых постараемся помочь мамам разобраться в море вопросов, которые их мучают:

? Так ли важны описанные проблемы? Нужно ли настаивать и обучать ребёнка обводке по контуру, раскрашиванию картинок? Для чего ребёнку-дошкольнику нужно учиться аккуратно обводить фигуры, закрашивать картинки, не выезжая за контуры, рисовать простейшие фигуры самостоятельно?

Все эти упражнения готовят руку к будущему письму. Красивый почерк в будущем и лёгкое овладение письмом зависит от того, насколько хорошо малыш сможет своевременно овладения карандашом и ручкой, научиться регулировать нажим и плавную работу руки при письме.

Когда можно давать ребёнку письменные задания?

Оптимальный возраст, в котором ребёнку уже можно предлагать обводить простые геометрические фигуры и закрашивать картинки с минимальным количеством деталей — 3 года. Как всегда, напоминаю, что возраст этот – условный и зависит от того, насколько готов ваш малыш и какая была проведена подготовительная работа. Например, своим малышам я предлагаю обводить по точкам буквы в 2-2,5 года, делаем мы это в игре «Обводилки» (о неё я рассказываю на своём авторском курсе ).

Как научить малыша правильно держать в руке карандаш?

Чем меньше ребёнок и слабее развита моторика руки, тем крупнее должен быть рисунок для обводки и толще «инструмент» — толстый карандаш (лучше всего — мягкий или акварельный) или фломастер (большинство детей предпочитают именно их)! Обычные цветные карандаши не так хороши для малышей, поскольку для рисования ими требуется больший нажим. Кроме того, неразработанной ручке крохи сложно захватывать тонкий ствол карандаша (а тем боле, делать это правильно!).

Для формирования правильного захвата существуют толстые трёхгранные карандаши (короткие лучше не берите).

Появились в продаже и специальные накладки на обычные карандаши и ручки.

К слову, о ручках: сейчас в магазинах канцтоваров можно приобрести ручки-тренажёры. Их особенность в специальном прорезиненном утолщении с выемками для правильной постановки пальцев по время письма. Малышей привлечёт ручка с такой забавной фигуркой:

Тем, кто постарше, подойдут ручки попроще. Обратите внимание — есть такие ручки для левшей и для правшей.

Как правильно обучать ребёнка обводке по контуру?

Начните обучение с рисования по точкам сначала прямых, а затем волнистых линий и простых геометрических фигур. На следующем этапе предложите ребёнку рисование по точкам животных и их раскрашивание.

Перед тем, как приступить к письменным заданиям, обязательно проведите пальчиковую игру гимнастику.

Самое главное в этом возрасте — простота, доступность, дозированность таких занятий. И, конечно же, обязательное условие для вовлечения малыша – игровая форма.

Мы не просто даём указание обвести круг, а просим помочь солнышку засиять и обогреть замёрзших зайчат – обвести его и нарисовать яркие лучики фломастером. Не требуем раскрасить квадрат, а предлагаем покрасить будку для грустной собачки, чтоб она стала красивой и яркой, а собачка- радостной.

На первых порах делать обводку можно вместе с малышом, рука в руке.

Действуйте при этом очень мягко, не сжимайте руку ребёнка, старайтесь не причинять ему дискомфорт – это может отбить у малыша желание заниматься в дальнейшем. С некоторыми детьми приходится предварительно наладить тактильный контакт — поиграть в игры типа ладушек, сделать массаж пальчиков. Хороший приём: пусть пальчики мамы поздороваются с пальчиками малыша, прикасаясь к ним по очереди.

Обведите одну-две фигуры вместе, а затем отпустите ручку малыша и предложите сделать то же самое самостоятельно. Ещё один хороший приём – обводка пальчиком. Перед тем, как малыш возьмёт в руки карандаш, предложите его пальчикам прогуляться по рисунку, который нужно обвести – покажите сами, как можно обвести фигуру пальцем, чтобы почувствовать её.

После того, как элементарные линии и фигуры будут усвоены, предложите ребёнку рисование по точкам животных и их раскрашивание. Подробнее про закрашиванием фигур и пользу раскрасок мы поговорим в следующий раз.

Надеюсь, эти советы помогут вашему малышу укротить карандаши и научиться делать обводку и рисовать простые фигуры самостоятельно.

Вы находитесь в категории раскраски Соедини по точкам. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски Соедини по точкам и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему Соедини по точкам развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.

«Умелые ручки » — графические упражнения на развитие мелкой моторики рук.
Куриленко Татьяна Алексеевна, учитель-логопед МДОУ д/с «Земляничка»р.п. Посевная, Черепановского района, Новосибирской области.
Описание: Рекомендация посвящена проблемам развития тонкой моторики, ловкости и координации. В ней предложены коррекционно-развивающие упражнения и задания, способствующие подготовке руки к письму.
Назначение: Материал предназначен для родителей подготовительной к школе группы.
Цель: развивать начальные графические навыки через коррекционно-развивающие упражнения и задания, способствующие подготовки руки к письму
Задачи:
1. развивать зрительно-моторную координацию движений и зрительно-пространственные представления;
2.развивать крупную (кистевую) и мелкую (пальцевую) моторику, право- и левостороннюю ориентацию, внимание;
3. формирование интереса к выполнению графических упражнений и заданий;
4.воспитывать чувство коллективизма при выполнении совместных действий.
Тренировка движений пальцев и кисти рук является важнейшим фактором, стимулирующим речевое развитие ребенка, способствующим улучшению артикуляционных движений, подготовке кисти руки к письму и, что не менее важно, мощным средством, повышающим работоспособность коры головного мозга, стимулирующим развитие мышления ребенка. Реализация упражнений позволит развить и совершенствовать точные движения пальцев рук и скоординировать ловкость движений. Для формирования у ребенка графического навыка необходимо обучать его с помощью системы специальных упражнений.

Для развития графического навыка следует использовать:
рисование линий: прямые дорожки, фигурные;
рисование по точкам, по контурам по клеточкам;
выполнения штриховок: с различным направлением движения руки, силуэтных штриховок.

Необходимо сразу учить ребенка правильным приемам действия:
вести линию сверху вниз и слева направо;
уметь выполнять линии различной толщины и формы;
штриховать ровно и без пробелов, не выезжая за контур.
При выполнении упражнений следует обращать внимание на:
правильность посадки за столом;
выполнение нужно начинать с простых заданий и постепенно повышать сложность.

Регулярные занятия с ребенком обеспечат правильное и красивое письмо.
Специальные упражнения на развитие графических навыков
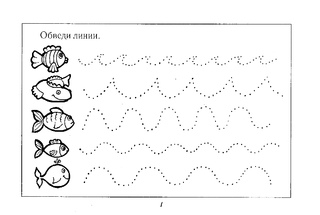
Прямые дорожки
Ребенка просят провести линию посередине прямой дорожки, не съезжая с нее и не отрывая карандаша от бумаги.
Фигурные дорожки
Ребенка просят провести фигурную дорожку, при прохождении дорожки ребенку следует стараться, как можно более точно следовать всем изгибам и поворотам линии.
Карандаш не должен отрываться от бумаги, и лист во время выполнения задания не переворачивается.

Рисование по точкам
Ребенка прося соединить точки согласно инструкции под рисунками. Карандаш не отрывается от листа бумаги, лист фиксируется и его положение не изменяется.

Рисование по контурам
Ребенка просят соединить точки для того, чтобы получился завершенный рисунок.

Рисование по клеточкам
На бумаге в клеточку ребенка просят продолжить узор по заданному образцу.

Выполнение штриховок (с различным направлением движения руки)
Ребенка просят выполнить различные виды штриховок по образцам:
вертикальные (сверху вниз)
горизонтальные (слева направо)
наклонные
«клубочками» (круговые движения руки)
полукругами.
Линии должны выполняться одним движением кисти руки. Штриховки вначале должны быть крупными, по мере приобретения ребенком навыка выполнения их размер уменьшается.

Пальчиковая гимнастика для развития мелкой моторики рук
Игры и упражнения с пальцами рук представлены в литературных источниках в разных вариантах.

Освоение предметных действий
Для развития тонкой моторики можно использовать упражнения с применением мешочка с песком, мяча. В зависимости от индивидуальных возможностей ребенка характер манипуляций с предметами можно варьировать, используя такие приемы как перекладывание, подбрасывание, ловля: изменяя темп работы и степень ее сложности, количество одновременно задействованных предметов. Ребенку с недостаточной сформированностью мелкой моторики рук, освоение предметных действий вызывает трудности.

Помните! Развитие тонкой моторики стимулирует развитие интеллектуальных способностей в целом! Не пренебрегайте графическими упражнениями — эти задания помогут вашему ребенку не только научиться писать, но и подготовиться в целом к обучению в школе.

Трафареты обведи по контуру. Раскраска обведи по контуру

/ Рисуем по точкам / Обведи по контуру

Распечатать раскраски по точкам. Соедини точки, нарисуй и раскрась

Если не началась автоматическая скачка, то чтобы скачать раскраску Рисуем по точкам , кликните по картинке кнопкой мыши и выберите «Сохранить изображение».

Остальные раскраски этого раздела

Обведи по контуру — скачать и распечатать раскраску. Обведи по контуру рисунки и раскрась, развитие моторики, подготовка к письму

Раскраски по точкам. Соедини точки, нарисуй и раскрась. Детский специализированный на раскрасках сайт. Уникальный авторский контент. Распечатать раскраски по точкам. Соедини точки, нарисуй и раскрась
Смежные проекты: сказки онлайн для детей

Детская косметика. Косметичка для маленьких принцесс

Говорят, что в женской сумке есть все. Практически все, что может понадобиться в любой ситуации. В этом есть часть правды. Как правило, в женской сумке есть множество различный вещей: расческа, лекарства, духи, блокнот, множество дисконтных и рекламных карточек, маникюрный набор и конечно косметичка. Кто-то носит с собой косметику всегда и везде, из-за того, что должность обязывает выглядеть на все сто и практически постоянно быть на людях. Другие наоборот, берут её редко или обходятся лишь помадой. Это все зависит от того, как именно, представительница прекрасного пола, относиться к макияжу.

у ребёнка не получается обводить фигуры по контуру,
отказывается выполнять такие задания, как обводка и раскраски,
не любит рисовать, не хочет рисовать карандашами,
не умеет держать ручку-карандаш в руке.

Я подготовила ряд статей, в которых постараемся помочь мамам разобраться в море вопросов, которые их мучают:

Когда можно давать ребёнку письменные задания?

Как научить малыша правильно держать в руке карандаш?

Для формирования правильного захвата существуют толстые трёхгранные карандаши (короткие лучше не берите).

Появились в продаже и специальные накладки на обычные карандаши и ручки.

Тем, кто постарше, подойдут ручки попроще. Обратите внимание — есть такие ручки для левшей и для правшей.

Как правильно обучать ребёнка обводке по контуру?

Перед тем, как приступить к письменным заданиям, обязательно проведите пальчиковую игру гимнастику.

На первых порах делать обводку можно вместе с малышом, рука в руке.

Обведи по контуру Утенка

Обведи по контуру Козленка

Обведи по контуру Щенка

Обведи по контуру Лягушку

Обведи по контуру Зайчика

Обведи по контуру Поросенка

Обведи по контуру Червяка

Обведи по контуру Ослика

Обведи по контуру Крота

Обведи по контуру Барашка

Обведи по контуру Лошадку

Обведи по контуру Киску

Обведи по контуру Мышку

Вы находитесь в категории раскраски Соедини по точкам.

Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски Соедини по точкам и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему Соедини по точкам развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.

Чтобы подготовить руку к письму, научиться правильно держать карандаш, умело на него нажимать и научиться рисовать линии разной формы, поможет рисование по точкам. Начинать обучаться рисовать по точкам лучше с обычных линий и геометрических фигур, а далее переходить к животным.

Рисование по точкам для детей 3-7 лет

Рисование по точкам называется графомоторикой. Для взрослых кажется совсем просто обвести рисунок по точкам. У маленьких детей еще не до конца развито пространственное мышление. Поэтому детские руки и мозг функционируют по-другому. Они не в состоянии сразу определить, что нарисовано на картинке, если соединить все точки, и должны потратить немало сил, чтобы получить картинку.

Простой рисунок

Для развития этой способности придумано рисование по точкам, которое для ребенка является практически чем-то волшебным. Сначала был обычный белый лист бумаги, где в хаотичном порядке располагались точки, а потом на нем появилось красивое изображение. Может получиться и ягодка, и цветочек, и машинка, и кошка, и собака, а также другие интересные и забавные рисунки, которые впоследствии можно еще и закрасить.

Для самых маленьких подойдут простые картинки с небольшим количеством линий: цветок, звезда, гном. Для детей постарше, лет с трех — четырех, лучше подбирать картинки с сюжетом и большим количеством точек. Например, целый букет цветов или елка с грибной полянкой. Существуют макеты, которые содержат большое количество точек, каждая из них имеет свой номер. Такие изображения рисуются в определенном порядке: при соединении точек необходимо соблюдать их номер.

Обратите внимание! Существуют специальные пособия, в которых по точкам зашифрованы слова и цифры. Они больше подойдут для подготовки малыша к школе. Их можно применять для изучения цифр, букв и написания слов. Картинки обводятся по точкам, начиная путь от самой маленькой цифры по порядку к самой большой.

Данная практика позволит в дальнейшем облегчить освоение прописи. У ребенка будет наработана рука, благодаря чему ему будет легче писать диктанты.

Ниже прилагается образец пронумерованного рисунка, который позволит развивать способности к математике.

Пронумерованный рисунок

Для чего нужно, что развивает

Рисование по точкам развивает различные навыки и умения:

развитие мелкой моторики рук у малыша;
развитие глазомера;
выработка навыков ориентации на листе;
развитие образного и пространственного мышления, воображения и фантазии;
способствует развитию речи: ребенок будет пытаться объяснить родителям, какая у него получилась картинка;
обведение картинок с цифрами учит ребенка считать.

Важно! Такой тип рисования может увлечь и взрослого. Вместе с малышом родители будут рисовать и разукрашивать получившуюся картинку. Такие совместные занятия играют важную роль в воспитании ребенка. Они помогут больше узнать о малыше, выявить его склонности и способности.

Рисование по точкам для детей 6-7 лет станет не только увлекательным занятием и интересным проведением времени, но и будет хорошей подготовкой ребенка к школе, научит его правильно или карандаш. Он научится проводить прямые и кривые линии. Для него это будет одновременно игрой и развивающим занятием. Рисование по точкам знакомит малыша с новыми предметами, разными дикими и домашними животными, предметами обихода, одеждой и т. д.

Рисование по точкам, постепенное развитие навыков

С раннего возраста дети начинают тянуться ко всему необычному. Им интересно все, что их окружает. Желательно, чтобы такое познание происходило в форме игры. По советам психологов при занятиях с детьми необходимо использовать больше наглядных и красочных пособий, которые будут развивать не только его навыки, но и удовлетворять потребности в игре.

Обратите внимание! Соединение линий служит в качестве руководства: в любое время скорость движения можно уменьшить, сделать сильнее или слабее нажатие на карандаш, не испортив рисунок.

Когда ребенку предлагается распечатанный материал с рисунком, на котором необходимо нарисовать что-то по точкам, для начала необходимо попросить его обвести указательным пальцем линии своей правой руки. Если ребенок левша, то левой рукой. Затем малыша необходимо попросить нарисовать линию не на листе, а над картинкой в воздухе. Упражнение выполняется несколько раз (четыре — пять раз), а затем можно приступить к рисованию карандашом. После того, как ребенок освоит обведению карандашом, ему необходимо предложить рисовать маркером или ручкой.

После того, как ребенок освоит рисование по точкам различные линии, прямые, волны, можно начинать рисовать более сложные картинки: фигуры, а затем животных. Различные изгибы линий развивают навык рисования, что позволяет изучать правописание различных цифр и букв.

Различные варианты пособий с разными рисунками легко найти в магазинах или скачать онлайн из интернета образцы и распечатать. Также картинку по точкам можно создать собственными руками, используя чистый лист бумаги формата А4, зубочистку и чернила или краски. Для его изготовления необходимо следующее:

Обычным карандашом на листе нарисовать контуры рисунка.
Смочить зубочистку в чернилах или краске.
Расставить смоченной зубочисткой точки.
Стереть стирательной резинкой нарисованный карандашом контур.

Рисовать по точкам можно как дома, так и в детском саду, где следить за процессом будут родители или воспитатели соответственно. Достаточно усадить ребенка за стол, дать задание обвести по точкам картинку, показать, как это делается и предоставить малышу полную свободу.

Важно! Необходимо следить, чтобы ребенок правильно держал карандаш, в противном случае это может испортить почерк в будущем.

В первую очередь, стоит давать рисунки любимых героев мультфильмов. Для ребенка картинки должны быть интересными и соответствовать его возрасту. Например, для медвежата и котята становятся не такими уж интересными. Им хочется нарисовать любимого героя мультфильма.

Ниже представлены простые рисунки, в которых необходимо, соединяя точки, просто проводить линии от одного рисунка к другому. Здесь необходимо стараться не заезжать за края.

Сюжетный рисунок

Как еще развить мелкую моторику, кроме рисования по точкам

Если малыша, по каким-то причинам не заинтересовало рисование по точкам, ему можно подобрать и другие занятия, которые будут развивать его мелкую моторику. К ним относятся следующие:

Нанизывание крупного бисера на нитки.
Перебирание руками бус.
На стену можно приклеить бумагу или кусок старых обоев. Пусть ребенок потренируется что-то на нем нарисовать. На вертикальной поверхности рисовать гораздо сложнее, поэтому ручки будут тренироваться быстрее.
После того, как ребенок научиться держать в руках мелкие предметы и не отпускать их длительное время, стоит начинать его учить завязывать шнурки, плести косички из лент, веревочек.
Можно предложить ребенку обвести маркером заголовки в газетах или журналах.
Перекладывание бобов или горошин из одной емкости в другую, используя только два пальца, а не всю руку. Такая тренировка разовьет хорошее сцепление большого и указательного пальцев.
Можно рисовать указательным пальцем на запотевшем или замороженном окне.

Обратите внимание! Все перечисленные способы позволят развить мелкую моторику и помогут быстрее освоить малышу технику письма.

Когда ребенок начинает подрастать, ему надоедают простые игры с игрушками. В возрасте 6 лет уже необходимо готовиться к школе. Чтобы подготовка для него была интересной и в то же время полезной, можно использовать рисунки по точкам. Они разовьют мелкую моторику, помогут изучить цифры, буквы. Малыш с пользой и интересом проведет свой досуг.

Обведи по контуру большой маленький. Упражнения по развитию графических навыков ребенка. Раскраска Обведи по контуру

у ребёнка не получается обводить фигуры по контуру,
отказывается выполнять такие задания, как обводка и раскраски,
не любит рисовать, не хочет рисовать карандашами,
не умеет держать ручку-карандаш в руке.

Я подготовила ряд статей, в которых постараемся помочь мамам разобраться в море вопросов, которые их мучают:

Когда можно давать ребёнку письменные задания?

Как научить малыша правильно держать в руке карандаш?

Для формирования правильного захвата существуют толстые трёхгранные карандаши (короткие лучше не берите).

Появились в продаже и специальные накладки на обычные карандаши и ручки.

Тем, кто постарше, подойдут ручки попроще. Обратите внимание — есть такие ручки для левшей и для правшей.

Как правильно обучать ребёнка обводке по контуру?

Перед тем, как приступить к письменным заданиям, обязательно проведите пальчиковую игру гимнастику.

На первых порах делать обводку можно вместе с малышом, рука в руке.

Обведи по контуру Утенка

Обведи по контуру Козленка

Обведи по контуру Щенка

Обведи по контуру Лягушку

Обведи по контуру Зайчика

Обведи по контуру Поросенка

Обведи по контуру Червяка

Обведи по контуру Ослика

Обведи по контуру Крота

Обведи по контуру Барашка

Обведи по контуру Лошадку

Обведи по контуру Киску

Обведи по контуру Мышку

Рисование по точкам для детей линий, фигур и животных. Рисуем по точкам для развития навыка письма.

Красивый подчерк и успешное обучение письму зависит от правильного владения карандашом, умелого нажима и способности проводить линии всевозможной формы. Начните с обучения рисованию по точкам линий и фигур, а затем предложите ребёнку рисование по точкам животных и их раскрашивание.

Рисуем по точкам, развивая навыки постепенно

Проведение линий карандашом или ручкой — отличная практика, помогающая приучить руку к письму, развить мелкие мышцы, научить малыша что-то крепко удерживать.

Пунктирная линия служит в качестве руководства и помогает ребёнку, ведь в любой момент можно замедлить скорость рисования, усилить или ослабить нажатие на карандаш, не испортив картинку, а, следовательно, не потеряв интерес.

Как только ребёнок научится рисовать по точкам линии, прямые и всевозможные волны, переходите к фигурам, а затем к животным. Изгибы пунктирных линий разовьют навык рисования достаточно для того, чтобы начать изучение правописания букв и цифр.

Предлагая ребёнку распечатанный материал с картинкой, на которой требуется нарисовать что-нибудь по точкам, сначала попросите малыша обвести линии указательным пальцем его правой руки (или левой, если ребёнок — левша). Затем попросите его рисовать пальцем не по листу, а словно в воздухе над картинкой. Повторите упражнение несколько раз, а потом выполните задание карандашом.

Когда ребёнок научится рисованию по точкам карандашом, предложите ему ручку или маркер.

Уделите внимание рисованию по точкам животных, без отрыва руки от бумаги.

Как ещё развить мелкую моторику, кроме рисования по точкам?

Если ваш ребёнок по каким-либо причинам не заинтересовался материалами рисования по точкам, вы можете весело провести время, развивая мелкую моторику и другими способами.

Нанизывайте вместе крупный бисер на ниточки или перебирайте бусы;
Приклейте большой лист бумаги или старые обои на стену и пусть ваш ребёнок рисует свои картинки на этом листе. Рисование на вертикальной поверхности требует прикладывания больших усилий и ручки тренируются быстрее;
Как только ваш ребёнок уже достаточно крепко умеет держать в руках мелкие вещи и не отпускает их, если слегка потянуть, начинайте его учить завязывать шнурки или плести косички из любых лент или верёвочек;
Если вы читаете газеты или журналы, дайте ребёнку маркер и предложите ему обвести им все заголовки;
Хорошее сцепление большого и указательного пальцев проще всего развить, перекладывая бобы или даже горошинки из одной миски в другую, используя только два пальца, а не всю ладошку.
Морозные окна или запотевшие зеркала в ванной — отличное место для того, чтобы учиться рисовать указательным пальцем.

При желании, вы можете использовать в повседневной жизни каждый из способов развития мелкой моторики вашего ребёнка, этим вы поможете ему быстрее научиться писать в будущем.

Для развития мелкой моторики рук следует использовать:
пальчиковую гимнастику;
упражнения на освоение предметных действий.
При выполнении различных видов заданий, ребенок приобретает опыт графических движений. Необходимо сразу учить ребенка правильным приемам действия:
вести линию сверху вниз и слева направо;
уметь выполнять линии различной толщины и формы;
штриховать ровно и без пробелов, не выезжая за контур.
При выполнении упражнений следует обращать внимание на:
правильность посадки за столом;
выполнение нужно начинать с простых заданий и постепенно повышать сложность.

Карандаш не должен отрываться от бумаги, и лист во время выполнения задания не переворачивается.

Рисование по контурам
Ребенка просят соединить точки для того, чтобы получился завершенный рисунок.

Рисование по клеточкам
На бумаге в клеточку ребенка просят продолжить узор по заданному образцу.

Обведи по точкам грибы и ягоды.

Рисование по точкам. Раскраска по точкам

Рисование по точкам для детей линий, фигур и животных. Рисуем по точкам для развития навыка письма.

Рисуем по точкам, развивая навыки постепенно

Когда ребёнок научится рисованию по точкам карандашом, предложите ему ручку или маркер.

Уделите внимание рисованию по точкам животных, без отрыва руки от бумаги.

Как ещё развить мелкую моторику, кроме рисования по точкам?

Нанизывайте вместе крупный бисер на ниточки или перебирайте бусы;
Приклейте большой лист бумаги или старые обои на стену и пусть ваш ребёнок рисует свои картинки на этом листе. Рисование на вертикальной поверхности требует прикладывания больших усилий и ручки тренируются быстрее;
Как только ваш ребёнок уже достаточно крепко умеет держать в руках мелкие вещи и не отпускает их, если слегка потянуть, начинайте его учить завязывать шнурки или плести косички из любых лент или верёвочек;
Если вы читаете газеты или журналы, дайте ребёнку маркер и предложите ему обвести им все заголовки;
Хорошее сцепление большого и указательного пальцев проще всего развить, перекладывая бобы или даже горошинки из одной миски в другую, используя только два пальца, а не всю ладошку.
Морозные окна или запотевшие зеркала в ванной — отличное место для того, чтобы учиться рисовать указательным пальцем.

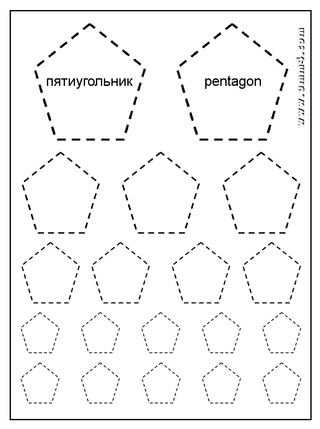Вы можете скачать раскраски Соедини по точкам и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему Соедини по точкам развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.

Когда дети достигают возраста 4-5 лет, игры с игрушками начинают надоедать, малыш развивается, ему необходимо подготавливаться к школе. А чтобы подготовка была одновременно полезной и интересной можно использовать точечные рисунки для подготовки руки к письму, развития мелкой моторики.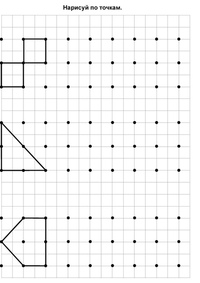 Рисование по точкам – интересное и полезное времяпрепровождение.

Взрослым кажется, что совсем не сложно обвести линии уже готового рисунка. Многие родители считают, что это просто развлечение для детей. Но малышам нужно потратить много сил, чтобы рисовать точечные фрукты, цифры или буквы.

Мозг и руки детей работают несколько иначе, чем у взрослых, поэтому им очень трудно сразу освоить обводилки и рисовать все точно. Но зато потом, в школе такая практика значительно облегчит освоение прописи, ребенку будет проще написать диктант. Ребенку будет проще писать диктант, потому что его рука уже будет натренирована.

Такое занятие как рисование по точкам называется графомоторикой. Обводилки развивают очень много навыков и умений. Ими наделены прописи. Там есть картинки, которые нужно рисовать и многое другое. Задание звучит как «соедини точки и получи рисунок» либо просто «соедини». Прописи – это печатные тетради. Обучение начинается с того, что ребенок обводит печатные прямые линии, буквы, учится рисовать простые рисунки.

Как развить мелкую моторику

Мелкая моторика – это правильные, скоординированные движения рук и ног. Мелкая моторика начинает развиваться с самого рождения. Сначала малыш начинает сжимать и разжимать кулачки, потом хватать и держать предметы, держать ложку и т.д. Чтобы правильно и красиво писать и рисовать, ребенку просто необходимо развивать мелкую моторику рук.

Это можно сделать с помощью самых разнообразных игр. Один из действенных способов – рисование по точкам. Сначала можно обводить просто линии, затем взяться за цифры и буквы. Научившись обводить линии, цифры и буквы, можно смело взяться за овощи и другие, более сложные фигуры. Таким образом вырабатывается техника письма и ребенок учится рисовать.

Веселые занятия для детей! Соединяем рисунок по точкам

Раскраска по точкам

Для того чтобы распечатать кликните по картинке, она откроется в специальном окне, далее нажимаете правой кнопкой мыши по картинке и выбираете «Печать»

Это вид раскраски, где на рисунке изображены фрукты, овощи, люди, цифры или буквы, но линии этих рисунков выполнены в виде точек. Ребенок должен обвести эти точки, чтобы получилась картинка, а потом можно ее раскрасить. Школьные прописи содержат такие рисунки, но там чаще представлены линии, цифры и буквы. Прописи не только учат правильно писать, но и помогают запомнить алфавит. Ведь алфавит это самое главное, что должен знать будущий ученик. Цифры предлагается обвести в клетках, а буквы по линиям.

Такие задания могут заинтересовать детей. Рисование по клеточкам тоже очень нравится детям. Зачастую в клеточках написаны цифры, а каждой цифре соответствует определенный цвет. Заполняя все клеточки, малыш получает рисунок. Также примером такого рисования являются японские кроссворды.

Соедини по точкам

Для детей в возрасте 4-5 лет соединение по точкам – интересное занятие. В 4-5 лет малышей трудно заинтересовать учебой, заставить читать или писать диктант. Но достаточно лишь распечатать прописи с точками, как у детей просыпается интерес. На первый раз лучше просто предложить обвести прямые линии, затем цифры, буквы и другие фигуры.

Такие картинки помогут выучить алфавит, кстати, ребенку будет проще писать печатные буквы т.к. их линии более прямые. После прохождения такой темы как алфавит, можно устроить небольшой диктант, чтобы посмотреть насколько хорошо он усвоил алфавит. Диктант можно провести и для проверки цифр.

Обведи по контуру и раскрась

Все рисунки по точкам для детей имеют одно и то же задание: соедини, обведи рисунок и раскрась. Прописи тоже наполнены такими заданиями как: соедини точки. Прописи – это печатные тетради для дошкольников (от 2 до 6 лет) и младших школьников (от 6 до 9 лет). В прописях можно только учиться писать отдельные буквы, а, например, диктант стоит писать в другой тетради. В них вырабатывается техника письма.

Детям в возрасте 3-5 лет можно распечатать картинки, которые они смогут соединить. Это будет интересным заданием для них. Зачастую такие картинки имеют два задания: соедини и раскрась. Если у родителей нет возможности распечатать картинки, можно их нарисовать самостоятельно, но мы рисуем не так точно как компьютер, особенно всякие фигуры, овощи и т. п.

Алфавит

Прописи предлагают ребенку, чтобы он мог выучить алфавит не только в устном, но и в письменном виде. Некоторые авторы прописей предлагают проводить с детьми диктант, чтобы проверять их знания. Диктант – это отличная проверка знаний, скорости письма.

Цифры

Цифры предлагается обводить в клетках, чтобы ребенок сразу привыкал к такой технике записи. Цифры писать проще, чем буквы, они содержат больше прямых линий. Хотя детям и не очень нравятся математические рисунки, они кажутся им скучными, потому что их нельзя раскрасить.

Животные

Животные вызывают больший интерес у детей. Такие картинки можно раскрасить, увидеть новое животное, соединив точки, выучить много видов животных, которые раньше были неизвестны ребенку.

Выбор остается всегда за родителями. Только они вправе решать готов ли их малыш к заданию «соедини», какие картинки лучше подобрать для соединения, что малыша больше заинтересует. Возраст 4-5 лет это очень важный этап в жизни маленького человека. Уже в 5 лет он знает, что ему интересно, решает, чем он будет заниматься.

В 5 лет ребенок уже активно готовится к школе. Помогайте своим детям во всем, если есть задание «соедини» – покажите как, «запомни» – подберите самый легкий способ. В 5 лет малыши очень нуждаются в вашей помощи и поддержке. Обводилки очень полезны для детей, они помогают в развитии мелкой моторики рук, усидчивости, внимательности и памяти.

Детские игры онлайн для детей. Рисунки по точкам Корабль онлайн

Я рисую на асфальте!

Рисуем мелками на асфальте для общего развития

Развивающие игры для всех
Рисование мелками на асфальте – отличный способ позабавиться с пользой. Придумать интересные, познавательные игры вам поможет наша коллекция идей. Рекомендуем запастись влажными салфетками и порцией хорошего настроения! Не забудьте про соответствующую экипировку для себя и ребенка (будьте готовы к испачканной одежде, отсутствую каблуков и перепачканным мордашкам) – отсидеться на скамейке на этой прогулке явно не удастся.
1. Нарисуй тень
Цель игры: обрисовать чужую тень. Можно сделать несколько «замеров» с одного и того же предмета/человека в одном и том же месте, но в разное время суток.
Этот опыт наглядно продемонстрирует, как меняется тень в зависимости от времени суток и положения солнца.
2. Обведи по трафарету
Цель игры: обвести букву, цифру, любой предмет, вырезанный из плотного картона. Дополнительно, можно попросить малыша закрасить изображение, стараясь не выходить за контур.
Игра тренирует моторику и воображение.
3. Обведи по точкам
Цель игры: обвести букву, цифру, любой предмет по точкам. Можно не сообщать малышу, что именно вы изобразили точками, а предложить ему самому догадаться. Изображение выбирать простое, знакомое, учитывать возраст ребенка.
Игра тренирует моторику и воображение.
4. Дорисуй
Цель игры: превратить геометрические фигуры (для самых маленьких их рисует взрослый) в животных, предметы. Например, круг – апельсин, мячик, рыба – еж, чья-то голова и др.
Игра тренирует моторику и воображение.
5. Назови букву
Цель игры: назвать букву/цифру/геометрическую фигуру. Взрослый рисует на асфальте большие букву/цифры/геометрические фигуры, а ребенок ходит по их очертаниям и называет, что изображено.
Игра тренирует память и воображение, пространственное мышление.
6. Рисуем карту
Цель игры: нарисовать карту своей комнату/квартала/детского сада или школы.
Игра тренирует моторику, память, развивает пространственное ориентирование.
7. Пишем «приветы»
Цель игры: написать что-то, передать сообщение другу/соседу. Например, перед входом в подъезд можно написать «Добро пожаловать в подъезд №5!» или «Поздравляю с Днем рождения».
Игра тренирует моторику, орфографическую зоркость (писать нужно без ошибок!), воспитывает доброжелательность.
8. Лабиринты
Цель игры: нарисовать дорожки, лабиринты, по которым можно ходить, ездить на самокате, велосипеде. Можно делать остановки в специально обозначенных местах.
Игра тренирует моторику, воображение, координацию, пространственное ориентирование.
9. Дартс
Цель игры: используя мочалки для посуды, камешки, пробки попасть в обозначенный сектор.
Игра тренирует моторику, меткость.
10. Модное дефиле
Цель игры: используя одежду (ту, которую не жалко испачкать) нарядить нарисованных на асфальте модников (родители могут помочь малышам нарисовать силуэты детей). В принципе, можно даже обрисовать фигуры самих модельеров, только для этого им нужно лечь на асфальт.
Игра тренирует воображение.
11. Подарок для буквы
Цель игры: взрослый рисует мелом на асфальте букву, а ребенок дорисовывает подарок — предмет, который начинается с этой буквы.
Игра тренирует воображение, способствует запоминанию алфавита.

Игры для компании «мелковых» художников
1. Один ребенок рисует несколько животных или предметов на асфальте, а другой должен придумать историю про каждый предмет в отдельности. В эту игру может играть любое количество игроков, истории можно рассказывать по очереди.
2. Можно придумать заранее какую-нибудь тему и предложить детям нарисовать рисунки соответствующие ей. В этой игре могут быть победители, но лучше заранее позаботиться о мелких подарках для всех.
3. Совместными усилиями нарисовать мелом комикс, иллюстрацию к любимой сказке или картину.
4. Если есть возможность, то украсить рисунками скучный бетонный забор возле дома, стену заброшенного гаража или даже стволы деревьев.
5. На камнях нарисовать машинки, а на асфальтированной дорожке трассу для них. Чей автомобиль быстрее достигнет финиша?
6. Обвести лужу и придумать на кого она похожа, дорисовав недостающие детали. Каждый художник выбирает себе свою лужу или по очереди добавляет свой элемент к общему изображению.
7. Нарисовать на дорожке мелом следы какого-либо животного. Задача игроков — определить, что это здесь наследил и пройти по следам, изображая их «хозяина».
8. Игра в старые добрые крестики-нолики на асфальте — не надоедает и учит логически мыслить, достойно принимать проигрыш и думать на несколько ходов вперед.
9. Всем знакомые классики. Интерпретации могут быть любыми.
10. Если игроков несколько, то весело делать следующее. Выбирают ведущего, он закрывает глаза. Кто-то из детей обводит мелом на асфальте свою ладошку. Ведущий должен угадать чья рука.
Напоследок несколько веселых советов:
Часто бывает, что места на асфальте не остается: так много всего нарисовали дети! Можно в первый день что-то не дорисовать, а затем завершать свой «шедевр» в последующие дни.
Водяными пистолетами можно смывать рисунки на асфальте, а затем рисовать новые. Детям такая веселая уборка очень понравится!
Если вдруг вам станет мало листа бумаги, творческая душа захочет развернуться во… весь асфальт (!) вспомните про цветные мелки и скучно-серые дорожки возле дома. Айда на улицу, пока дождик не испортил наши планы! Пусть асфальт под ногами превратиться в холст, а фантазия не знает границ.

В «День Защиты Детей» 1 июня ребята и их родители поучаствовали дистанционно в конкурсе детского рисунка «Планета детства» приуроченному к этому празднику.

Желаем творческих побед!

9 самых распространенных форм и способы их определения

Вы, наверное, много узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.

В этой статье мы рассмотрим, что такое фигура, а также множество общих фигур, как они выглядят и основные формулы, связанные с ними.

Что такое форма?

Если вас спросят, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но «форма» тоже имеет особое значение. — это не просто названия кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.

Форма может иметь любой размер и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места.Трудно осознать это, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического пространства , такого как треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.

Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур — она двух- или трехмерная, потому что имеет форму.

Кубики, подобные тем, что здесь показаны, представляют собой трехмерные квадраты — обе формы!

6 основных типов двумерных геометрических фигур

Трудно изобразить форму только на основе определения — что значит иметь форму , но не занимать места? Давайте посмотрим на несколько различных форм, чтобы лучше понять, что именно значит быть формой!

Мы часто классифицируем формы по количеству сторон. «Сторона» — это отрезок линии (часть линии), составляющий часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.

Тип 1: эллипсы

Эллипсы — это круглые, овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.

Овал

Овал немного похож на размазанный круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная. Существует много-много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая имеет удлиненную форму, а не идеально круглую, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.

Поскольку овал не является идеально круглым, формулы, которые мы используем для их понимания, должны быть скорректированы.

Также важно отметить, что вычислить окружность овала довольно сложно , поэтому ниже нет уравнения окружности.Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией окружности, потому что даже лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.

Определения

Большой радиус : расстояние от начала овала до самого дальнего края
Малый радиус : расстояние от начала овала до ближайшего края

Формулы

Площадь = $ \ Major \ Radius * \ Minor \ Radius * π $

Круг

Сколько сторон у круга? Хороший вопрос! К сожалению, нет хорошего ответа, потому что «сторон» больше связаны с многоугольниками — двумерной формой как минимум с тремя прямыми сторонами и обычно как минимум с пятью углами. Большинство знакомых форм — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.

Итак, сколько сторон у круга? Нуль? Один? На самом деле это неактуально — вопрос просто не относится к кругам.

Круг — это не многоугольник, но что это такое? Круг — это двумерная форма (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одинаковом расстоянии от точки в центре. У овала два фокуса в разных положениях, а у круга всегда в одном и том же положении.

Определения

Начало: центр окружности
Радиус: расстояние от начала координат до любой точки на окружности
Окружность: расстояние по окружности
Диаметр: длина от одного края круга до другого
$ \ bo {π} $: (произносится как пирог) 3. 2

Тип 2: Треугольники

Треугольники — это простейшие многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.

Поскольку существует много видов треугольников, есть лот важных формул треугольника , многие из которых более сложные, чем другие.Основы включены ниже, но даже основы полагаются на знание длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете рассчитать его различные аспекты, используя углы или только некоторые из сторон.

Определения

Вершина : точка пересечения двух сторон треугольника
Основание : любая из сторон треугольника, обычно та, которая нарисована внизу.
Высота : расстояние по вертикали от основания до вершины, с которой не связано

Формулы

Площадь = $ {\ base * \ height} / 2 $
Периметр = $ \ side a + \ side b + \ side c $

Тип 3: параллелограммы

Параллелограмм — это форма с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами равной длины. Вы могли заметить, что это определение применяется к квадратам и прямоугольникам — это потому, что квадратов и прямоугольников также являются параллелограммами ! Если вы можете вычислить площадь квадрата, вы можете сделать это с любым параллелограммом.

Определения

Длина : размер нижней или верхней стороны параллелограмма
Ширина : размер левой или правой стороны параллелограмма

Формулы

Область : $ \ длина * \ высота $
Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 $
Альтернативно, Периметр : $ \ Сторона * 4 $

Прямоугольник

Прямоугольник — это форма с параллельными противоположными сторонами в сочетании со всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны. В прямоугольнике одна пара параллельных сторон длиннее другой, что делает его похожим на вытянутый квадрат.

Поскольку прямоугольник является параллелограммом, вы можете использовать те же формулы для вычисления их площади и периметров.

Площадь

Квадрат очень похож на прямоугольник, за одним заметным исключением: все его стороны равны по длине. Как и прямоугольники, квадратов имеют углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является разновидностью прямоугольника, который является разновидностью параллелограмма!

По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, как и для любого другого параллелограмма.

Ромб

Ромб — как вы уже догадались — разновидность параллелограмма. Разница между ромбом и прямоугольником или квадратом в том, что его внутренние углы на равны только , как их диагональные противоположности.

Из-за этого ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр рассчитывается таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.

Определение

Диагональ : расстояние между двумя противоположными вершинами

Формулы

Площадь = $ {\ Диагональ 1 * \ Диагональ 2} / 2 $

Тип 4: трапеции

Трапеции — это четырехгранные фигуры с двумя противоположными параллельными сторонами.В отличие от параллелограмма трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.

Определения

Основание : любая из параллельных сторон трапеции
Ножки : одна из непараллельных сторон трапеции
Высота : расстояние от одной базы до другой

Формулы

Область : $ ({\ Base_1 \ length + \ Base_2 \ length} / 2) \ altitude $
Периметр : $ \ Base + \ Base + \ Leg + \ Leg $

Тип 5: Пентагоны

Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленным внутрь, или вогнутым — с внутренним углом больше 180 градусов.

Поскольку форма более сложная, ее необходимо разделить на более мелкие формы, чтобы вычислить ее площадь.

Определения

Апофема : линия, проведенная от центра пятиугольника к одной из сторон, ударяющая в сторону под прямым углом.

Формулы

Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 $
Площадь : $ {\ Perimeter * \ Apothem} / 2 $

Тип 6: шестиугольники

Шестиугольник — это шестигранная форма, очень похожая на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.

Также, как и пятиугольники, формула площади шестиугольника значительно сложнее, чем формула параллелограмма.

Формулы

Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 + \ Сторона 6 $
Площадь : $ {3√3 * \ Side * 2} / 2 $
Альтернативно, Площадь : $ {\ Perimeter * \ Apothem} / 2 $

А как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — объем занимаемого пространства, а не только форма, — которое необходимо учитывать при вычислении площади и периметра.

Математика

, включающая 2D-формы, такие как приведенные выше, называется плоской геометрией , потому что она имеет дело конкретно с плоскостями или плоскими формами . Математика, включающая трехмерные формы, такие как сферы и кубы, называется твердотельной геометрией , поскольку она имеет дело с твердыми телами, что по-другому обозначает трехмерные формы .

Двумерные формы составляют трехмерные формы, которые мы видим каждый день!

3 основных совета по работе с фигурами

Существует так много типов фигур, что бывает сложно запомнить, что есть что и как рассчитать их площади и периметры. Вот несколько советов, которые помогут вам их запомнить!

# 1: Определить многоугольники

Некоторые формы являются многоугольниками, а некоторые нет. Один из самых простых способов сузить кругозор какой-либо формы — это выяснить, является ли это многоугольником.

Многоугольник состоит из прямых, не пересекающихся. Какие из представленных ниже фигур являются многоугольниками, а какие нет?

Круг и овал не являются многоугольниками, поэтому их площадь и периметр рассчитываются по-разному. Узнайте больше о том, как их вычислить, используя $ π $ выше!

# 2: Проверить параллельность сторон

Если фигура, на которую вы смотрите, представляет собой параллелограмм, обычно легче вычислить ее площадь и периметр, чем если бы это не параллелограмм. Но как определить параллелограмм?

Это прямо в названии — параллель. Параллелограмм — это четырехсторонний многоугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы — это параллелограммы.

Квадраты и прямоугольники используют одни и те же базовые формулы для вычисления площади длины, умноженной на высоту. Их также очень легко найти по периметру, поскольку вы просто складываете все стороны вместе.

С ромбами все усложняется, потому что вы умножаете диагонали и делите их на два.

Чтобы определить, на какой параллелограмм вы смотрите, спросите себя, все ли у него углы 90 градусов.

Если да, то квадрат или прямоугольник . Прямоугольник имеет две стороны, которые немного длиннее других, тогда как у квадрата все стороны равны. В любом случае, вы вычисляете площадь, умножая длину на высоту и периметр, складывая все четыре стороны вместе.

Если нет, то, вероятно, это ромб, который выглядит так, как если бы вы взяли квадрат или прямоугольник и наклонили его в любом направлении. В этом случае вы найдете площадь, умножив две диагонали вместе и разделив на два. Периметр определяется так же, как периметр квадрата или прямоугольника.

# 3: Подсчитайте количество сторон

Формулы для фигур, у которых нет четырех сторон, могут быть довольно сложными, поэтому лучше всего их запомнить. Если у вас возникли проблемы с их правильностью, попробуйте запомнить греческие слова для чисел, , например:

Tri : три, как в triple, что означает три чего-то

Tetra : четыре, как количество квадратов в блоке Tetris

Penta : пять, как в Пентагоне в Вашингтоне, округ Колумбия.C., представляющий собой большое здание в форме Пентагона

Hexa : шесть, как в шестнадцатеричном формате, шестизначные коды, часто используемые для цвета в веб-дизайне и графическом дизайне

Септа : семь, как в Септе, женском духовенстве религии Игры Престолов, имеющей семь богов

Octo : восемь, как в восьми лапах осьминога

Эннеа : девять, как в эннеаграмме, общая модель человеческих личностей

Дека : десять, как в десятиборье, в котором спортсмены завершают десять видов

Что дальше?

Если вы готовитесь к экзамену ACT и вам нужна дополнительная помощь по геометрии, ознакомьтесь с этим руководством по координатной геометрии!

Если вы больше относитесь к типу SAT, это руководство по треугольникам в разделе геометрии SAT поможет вам подготовиться к тесту !

Не можете насытиться математикой ACT? Это руководство по полигонам на ACT поможет вам подготовиться с помощью полезных стратегий и практических задач!

Изогнутые формы | SkillsYouNeed

Круги, эллипсы, параболы и гиперболы

Наша страница «Многоугольники» охватывает формы, состоящие из прямых линий, также известные как «плоские формы».На этой странице подробно рассказывается о фигурах с кривыми, особенно о двухмерных.

Двумерные изогнутые формы включают окружности, эллипсы, параболы и гиперболы, а также дуги, сектора и сегменты. Трехмерные изогнутые формы, включая сферы, цилиндры и конусы, описаны на нашей странице, посвященной трехмерным формам.

Двумерные изогнутые формы

Круги

Вероятно, наиболее распространенной двумерной изогнутой формой является круг.

Для работы с кругами (и другими изогнутыми формами) в геометрии важно понимать ключевые свойства круга:

Прямая линия, проходящая через центр круга, — это диаметр .
Половина диаметра составляет радиус .
Линия по краю круга — это окружность .

Любая точка на окружности круга находится на том же расстоянии от центра круга, что и любая другая точка на окружности.

Представляем π (pi)

π или пи — греческая буква. В математике он используется для обозначения определенной константы, которая также является иррациональным или бесконечным числом (подробнее см. Нашу страницу о специальных числах).

π имеет значение 3,142 (хотя, поскольку оно бесконечно, это приближение к его точному значению).

π важно, потому что оно используется для вычисления длины окружности и площади круга.

Длина окружности равна π x диаметра или 2 × π × радиус (сокращенно 2πr).

Площадь круга равна π × радиус ². Эта формула обычно сокращается до πr ²

Для получения дополнительной информации о площади см. Нашу страницу Расчет площади .

Секторы и сегменты

Секторы и сегменты — это «кусочки» круга.

Секторы имеют форму ломтика пиццы с изогнутым краем и каждой прямой стороной той же длины, что и радиус круга, или пиццы, из которой он был вырезан.Круговые диаграммы состоят из ряда секторов, размер которых зависит от размера отображаемых данных.

Сектор может быть любого размера, однако сектор, представляющий собой полукруг (180 °), называется полукругом , а сектор четверти круга (90 °) называется квадрантом .

Сегмент — изогнутая часть сектора, часть, которая остается, если вы удалите треугольник из сектора. Сегменты состоят из двух строк. Дуга (отрезок окружности круга — см. Ниже) и хорда — прямая линия, соединяющая два конца дуги.

Сектор — это часть круга, поэтому его площадь составляет часть площади всего круга. Чтобы вычислить площадь сектора, вам нужно знать его центральный угол, θ и радиус.

Затем можно рассчитать площадь сектора по следующей формуле:

πr ² × (θ ÷ 360)

Дуги

Участок окружности называется дугой .

Чтобы рассчитать длину дуги между точками A и B, вам необходимо знать угол в центре между точками A и B.θ (тета) — это символ, используемый для представления этого угла, образованного A и B. В нашем примере мы используем градусы для θ, но также можно использовать радианы.

Вам также необходимо знать радиус (r) дуги.

Поскольку во всем круге 360 °, длина дуги равна центральному углу (θ), деленному на 360, а затем умноженному на длину окружности всего круга (2πr).

2πr × (θ ÷ 360)

Пример:

r = 10 см, θ = 88 °, π = 3.14

Длина дуги = 2 x 3,14 x 10 x (88 ÷ 360) = 62,8 x 0,24 = 15,07 см .

градуса или радиана?

Наиболее часто используемой единицей измерения углов являются градусы, но вы также можете встретить вычисления, в которых угол измеряется в радианах. Это стандартная единица СИ для измерения углов. Для получения дополнительной информации о радианах см. Нашу страницу Introduction to Angles . Для получения дополнительной информации о системе измерения SI см. Нашу страницу о Системы измерения .

2π радиан равняется 360 °, поэтому формула для длины дуги, когда θ выражается в радианах, имеет вид просто rθ.

Эллипсы

Эллипс — это кривая на плоскости (или плоской поверхности), окружающая две точки фокусировки. Прямая линия, проведенная от одной точки фокусировки к любой точке кривой, а затем к другой точке фокусировки, имеет одинаковую длину для каждой точки кривой.

Эллипсы очень важны в астрономии и физике, так как каждая планета имеет эллиптическую орбиту с Солнцем в качестве одной из фокусных точек.

Круг — это особая форма эллипса, где две фокусные точки находятся в одном месте (в центре круга). Эллипсы также можно описать как «овальные», но слово «овал» гораздо менее точно используется в математике и означает просто «овальной формы».

Свойства эллипса:

Эллипс имеет две главные оси и симметричен относительно них.

Более длинная ось называется большой осью ; более короткая ось — это малая ось .

Четыре точки, в которых оси пересекают окружность, называются вершинами (особая вершина). Две точки, где малая ось пересекает окружность, называются совпадающими вершинами .

Две фокальные точки (или фокусы, иногда называемые локусами или локусами) находятся на большой оси и на равном расстоянии от центра.

Расстояние от одной точки фокуса до любой точки окружности и обратно до другой точки фокуса (синяя пунктирная линия на нашей диаграмме) такое же, как расстояние между вершинами на большой оси.

Степень удлинения эллипса определяется его эксцентриситетом . Формула для расчета эксцентриситета:

Эксцентриситет =	расстояние от центра до фокуса
	расстояние от центра до вершины по большой оси

Эксцентриситет круга равен нулю, потому что точки фокусировки находятся в одном и том же месте (центре) (мы также говорим, что они совпадают на ).Таким образом, расстояние от центра до фокальной точки равно нулю. Эксцентриситет увеличивается по мере того, как эллипс становится длиннее, но всегда меньше 1. Когда расстояние от центра до фокальной точки такое же, как расстояние от центра до вершины, тогда эллипс стал прямой линией и его эксцентриситет равно 1.

Площадь эллипса рассчитывается как π (½ x малая ось) (½ x большая ось).

Параболы, гиперболы и взаимосвязь между кривыми формами

Параболы и гиперболы — это скорее формы изогнутых форм, но их сложнее определить, чем круги и эллипсы.Они тесно связаны друг с другом, а также с кругами и эллипсами, потому что все они представляют собой конические сечения , , то есть формы, которые образованы путем разрезания конуса плоской плоскостью.

Характеристики конических сечений изучались на протяжении тысячелетий и представляли интерес для древнегреческих математиков, таких как Евклид и Архимед. На диаграмме ниже показан двойной конус, скорее похожий на песочный таймер.

Если плоскость разрезает конус под углом, параллельным основанию конуса (т.е.е. перпендикулярно его вертикальной оси), то образуется окружность (вверху слева).
Если плоскость разрезает конус параллельно стороне конуса , то образуется парабола (в центре).
Если плоскость разрезает конус под углом между этими двумя, так что он поддерживает контакт со сторонами конуса во всех местах, то образуется эллипс (внизу слева).
Если плоскость пересекает оба конуса под более вертикальным углом, то сечение представляет собой гиперболу .

Параболы и гиперболы — это симметричные кривые с единственной осью симметрии и вершиной (самая низкая точка U-образной кривой).

Все параболы имеют одинаковую характерную форму, независимо от их размера. По мере того, как вы уменьшаете масштаб все дальше и дальше от вершины к бесконечности, парабола меняет форму с чаши на форму шпильки, а ее руки становятся все ближе и ближе к параллельности.

В отличие от парабол, гипербол могут иметь различную форму , потому что угол разреза может широко варьироваться.И параболы, и гиперболы бесконечны, но руки гиперболы никогда не становятся параллельными.

Реальные применения конических секций

Конические секции могут применяться во многих реальных условиях.

Они используются в линзах для телескопов и отражателях в фарах или прожекторах для создания луча света.
Сложная математика, связанная с этими формами, жизненно важна при вычислении орбит спутников.
В технике тросы на мосту Золотые Ворота имеют форму идеальной параболы, а крылья самолетов имеют форму эллипсов.
В спорте дуга, по которой идет мяч для футбола, бейсбола или крикета, также является параболой, поэтому понимание конических сечений жизненно важно для анализа результатов игрока, что становится все более важным с деньгами, вложенными в профессиональный спорт.
Органическая форма этих форм также позволяет использовать их в искусстве и архитектуре.Примеры включают Cybertecture Egg в Мумбаи, Gateway Arch в Миссури и работы многочисленных скульпторов, такие как Torqued Ellipses Ричарда Серры в музее Гуггенхайма.

Необходимые навыки?

Круги являются частью базовой геометрии, и вам действительно нужно знать, как рассчитать их основные свойства.

Однако маловероятно, что вам нужно будет делать больше, чем знать о существовании других форм, если вы не хотите серьезно заняться инженерией, физикой или астрономией.

Тем не менее, вы можете обнаружить, что вам нравится знать, что вогнутые кривые градирни электростанции или свет от направленной вниз галогенной лампы имеют форму гиперболы.

Дополнительная литература по навыкам, которые вам нужны

Понимание геометрии
Часть необходимых навыков Руководство по счету

Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

Круг

Круг сделать легко:

Нарисуйте кривую на расстоянии
от центральной точки.

А так:

Все точки находятся на одинаковом расстоянии от центра.

Самостоятельно нарисовать

Вставьте булавку в доску, оберните вокруг нее веревку и вставьте в петлю карандаш. Держите веревку натянутой и нарисуйте круг!

Поиграй с ним

Попробуйте перетащить точку, чтобы увидеть, как меняются радиус и окружность.

(Посмотрите, сможете ли вы сохранить постоянный радиус!)

Радиус, диаметр и окружность

Радиус — это расстояние от центра наружу.

Диаметр проходит прямо по окружности через центр.

Окружность — это расстояние один раз по окружности.

А вот и действительно крутая вещь:

Когда мы разделим длину окружности на диаметр, мы получим 3,141592654 …
, что является числом π (Пи)

Итак, когда диаметр равен 1, длина окружности равна 3,141592654 …

Мы можем сказать:

Окружность = π × Диаметр

Пример. Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?

Пройденное расстояние = Окружность = π × 100 м

= 314 м (с точностью до м)

Также обратите внимание, что диаметр в два раза больше радиуса:

Диаметр = 2 × Радиус

Так же верно и то:

Окружность = 2 × π × Радиус

Вкратце:

× 2	× π

Радиус

Диаметр

Окружность

Вспоминая

Длина слов может помочь вам запомнить:

Радиус — кратчайшее слово и кратчайшая мера
Диаметр длиннее
Окружность самая длинная

Определение

Круг имеет плоскую форму (двумерный), поэтому:

Площадь

Площадь круга в π раз больше квадрата радиуса, что записывается:

A = π r ²

Где

A — это Площадь
r — радиус

Чтобы вспомнить, подумайте «Пирог в квадрате» (хотя пироги обычно круглые):

Пример: Какова площадь круга с радиусом 1.2 м?

Площадь = πr ²

= π × 1,2 ²

= 3,14159 … × (1,2 × 1,2)

= 4,52 (до 2 знаков после запятой)

Или, используя Диаметр:

A = ( π /4) × D ²

Площадь

по сравнению с площадью

Окружность составляет около 80% площади квадрата такой же ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%

И кое-что интересное для вас:

См. Площадь круга по линиям

Имена

Поскольку люди изучали круги в течение тысяч лет, у них появились особые имена.

Никто не хочет говорить «линия, которая начинается на одной стороне круга, проходит через центр и заканчивается на другой стороне» , когда они могут просто сказать «Диаметр».

Итак, вот самые распространенные специальные имена:

Линии

Линия, которая «просто касается» круга, когда проходит мимо, называется касательной .

Линия, пересекающая круг в двух точках, называется секущей .

Отрезок линии, который идет от одной точки к другой на окружности круга, называется хордой .

Если он проходит через центр, он называется диаметром .

Часть окружности называется дугой .

Ломтики

Есть два основных «кусочка» круга.

Кусочек «пиццы» называется сектором.

А отрезок, образованный аккордом, называется отрезком.

Общие сектора

Квадрант и Полукруг — это два особых типа сектора:

Четверть круга называется квадрантом .

Полукруг называется полукругом .

Внутри и снаружи

У круга есть внутренняя и внешняя стороны (конечно же!).Но у него также есть «включено», потому что мы можем оказаться прямо на круге.

Пример: «A» находится вне круга, «B» находится внутри круга, а «C» находится на круге.

Эллипс

Круг — это «частный случай» эллипса.

Что такое круг? — [Определение, факты и пример]

Учитесь с помощью полной программы обучения математике K-5

Что такое круг?

Круг — это круглая фигура без углов и краев.

В геометрии круг можно определить как замкнутую двумерную изогнутую форму.

Вокруг нас есть несколько вещей круглой формы: автомобильная шина, настенные часы, которые показывают время, и леденец на палочке.

Центр круга

Центр окружности — это центральная точка окружности, от которой все расстояния до точек окружности равны. Это расстояние называется радиусом круга.

Здесь точка P — центр окружности.

Полукруг:

Полукруг — это половина круга, образованная разрезанием всего круга вдоль отрезка прямой, проходящего через центр круга. Этот отрезок прямой называется диаметром круга.

Четверть круга:

Четверть круга — это четверть круга, образованная разделением круга на 4 равные части или полукруга на 2 равные части.

Четверть круга также называют квадрантом.

Интересные факты

Прямая линия — это круг с бесконечной площадью.
У круга может быть бесконечное количество линий симметрии.
Слово «энциклопедия» буквально означает «круг обучения».
Круг можно разделить поровну независимо от его размера.

Давайте споем!

Шины старой желтой машины.

Круглая крышка конфетной банки.

Часы висят на стене.

Кошка играет с красным мячом.

Сладкий шоколадный пончик, который я съел,

И целый яблочный пирог у меня на тарелке.

Блестящие пуговицы на моем платье.

Какая форма? Сделать предположение.

Они все круглые, как C-I-R-C-L-E.

Давайте сделаем это!

Вместо того, чтобы раздавать своим детям рабочие листы по геометрии, попросите ребенка наблюдать / определять предметы круглой формы, такие как браслет, дверная ручка или хула-хуп.

Вы также можете попросить ребенка выбрать круглый предмет, например браслет или хула-хуп, и показать / определить на нем центр круга. Попросите их показать вам, как можно образовать полукруг или четверть круга.

Сопутствующий математический словарь

сфера, площадь, периметр.

Окружности, треугольники, квадраты и прямоугольники — математика для 2-го класса

Узнайте об основных фигурах

Мы видим формы везде.

Мы видим их у себя дома, в школе и даже на детской площадке.

Вы видите круги, треугольники, квадраты и прямоугольники?

Это здорово! Давайте узнаем больше об этих формах. 😎

Круг

Окружность состоит из изогнутой линии, которая идет по кругу. У него без прямых сторон, и без углов.

Вот несколько примеров кругов.

Можете ли вы думать о других предметах, относящихся к кругу? 😀

Треугольник

Треугольник имеет 3 стороны и 3 угла.

сторон — прямые линии, составляющие треугольник.

углов — это точки пересечения двух линий.

Это треугольник.

В нашем примере стороны треугольника имеют одинаковую длину. Это составляет три равных угла .

Угол — это расстояние между двумя линиями, образующими угол.

Стороны и углы треугольника не всегда должны быть равны.Точно так же, как треугольники ниже.

Вы узнаете больше об этих типах треугольников позже.

Квадрат

У квадрата 4 равные стороны. Это означает, что его стороны имеют одинаковую длину. Он также имеет 4 угла , которые составляют 4 равных угла.

Это углы квадрата.

Вот примеры квадратной формы.

Какие еще квадраты вокруг вас? 😀

Прямоугольник

Прямоугольник имеет 2 короткие стороны и 2 длинные стороны .Он также имеет 4 угла , которые составляют 4 равных угла.

Это углы прямоугольника.

Давайте рассмотрим несколько примеров прямоугольных предметов в школе.

Какие еще прямоугольные объекты вам известны? 😎

Время испытания

Все ли квадраты прямоугольники?

Да! Все квадраты являются прямоугольниками 🤓, но не все прямоугольники являются квадратами!

Смотри и учись

Отличная работа по изучению основных форм.

Теперь вы практикуете то, что вы узнали.

открытых учебников | Сиявула

Математика

Наука

- Читать онлайн
- Учебники
  - Английский
    - Класс 7A
    - Марка 7Б
    - 7 класс (A и B вместе)
  - Африкаанс
    - Граад 7А
    - Граад 7Б
    - Граад 7 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 8A
    - Сорт 8Б
    - Оценка 8 (вместе A и B)
  - Африкаанс
    - Граад 8А
    - Граад 8Б
    - Граад 8 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 9А
    - Марка 9Б
    - 9 класс (A и B вместе)
  - Африкаанс
    - Граад 9А
    - Граад 9Б
    - Граад 9 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 4A
    - Класс 4Б
    - Класс 4 (вместе A и B)
  - Африкаанс
    - Граад 4А
    - Граад 4Б
    - Граад 4 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 5А
    - Марка 5Б
    - Оценка 5 (вместе A и B)
  - Африкаанс
    - Граад 5А
    - Граад 5Б
    - Граад 5 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 6А
    - Марка 6Б
    - 6 класс (A и B вместе)
  - Африкаанс
    - Граад 6А
    - Граад 6Б
    - Граад 6 (A en B saam)
- Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (безымянные версии)

Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. 2 [/ latex].2 [/ латекс].

круг : Двумерная геометрическая фигура, состоящая из множества всех тех точек на плоскости, которые одинаково удалены от другой точки.

радиус : отрезок линии между любой точкой окружности и ее центром.

Определение круга так же просто, как и его форма. Круг — это совокупность всех точек, находящихся на определенном расстоянии от центральной точки. Это определение дает нам понятие радиуса круга, который равен определенному расстоянию.

Поскольку мы знаем, что круг — это набор точек на фиксированном расстоянии от центральной точки, давайте посмотрим, как мы можем построить круг в декартовой координатной плоскости с переменными [latex] x [/ latex] и [latex] y [/ латекс]. Чтобы найти формулу для этого, предположим, что центром является точка [latex] \ left (a, b \ right) [/ latex]. Согласно формуле расстояния, расстояние [латекс] c [/ латекс] от точки [латекс] \ left (a, b \ right) [/ latex] до любой другой точки [латекс] \ left (x, y \ right ) [/ latex] составляет:

[латекс] \ displaystyle {c = \ sqrt {\ left (x-a \ right) ^ 2 + \ left (y-b \ right) ^ 2}} [/ latex]

Если теперь возвести это уравнение в квадрат с обеих сторон, мы получим:

[латекс] \ displaystyle {c ^ {2} = \ left (x-a \ right) ^ {2} + \ left (y-b \ right) ^ {2}} [/ latex]

Помните, что расстояние между центром [латекс] \ left (a, b \ right) [/ latex] и любой точкой [latex] \ left (x, y \ right) [/ latex] на круге — это фиксированное расстояние , который называется радиусом.{2}} [/ латекс]

Это общая формула для круга с центром [латекс] \ слева (a, b \ справа) [/ латекс] и радиусом [латекс] r [/ латекс]. Обратите внимание, что все, что мы сделали, это немного изменили уравнение формулы расстояния.

График окружности: Окружность с центром [латекс] \ влево (a, b \ вправо) [/ латекс] построена в декартовой плоскости.

Частей круга

Теперь, когда у нас есть алгебраическая основа круга, давайте свяжем его с тем, что мы уже знаем о некоторых различных частях круга.

Диаметр

Диаметр — это любая прямая линия, проходящая через центр круга. Он равен удвоенному радиусу, поэтому:

[латекс] d = 2r [/ латекс]

Окружность

Окружность — это длина пути по окружности. Алгебраически это дается как:

[латекс] c = 2 \ pi r [/ латекс]

или аналогично [latex] c = \ pi d [/ latex]. Число [латекс] \ пи [/ латекс] (пи) определяется этим соотношением. Это отношение длины окружности любого круга к его собственному диаметру.2 [/ латекс]

Обратите внимание, что радиус является единственным определяющим параметром для размера любого конкретного круга, и поэтому это единственная переменная, от которой зависит площадь.

Введение в эллипсы

Представьте себе уравнение эллипса как вытянутого круга.

Задачи обучения

Соедините уравнение для эллипса с уравнением для круга с коэффициентами растяжения

Основные выводы

Ключевые моменты

Эллипс и круг являются примерами конических сечений.2} = 1} [/ latex]
, когда большая ось эллипса горизонтальна.
Эллипс: Эллипс — это коническое сечение, образованное пересечением плоскости с прямым круговым конусом.
В большинстве определений конических сечений окружность определяется как частный случай эллипса, когда плоскость параллельна основанию конуса. Однако также можно начать с определения круга и использовать графические преобразования, чтобы прийти к общей формуле для эллипса.2 = 1 [/ латекс]
Чтобы превратить его в эллипс, мы должны исказить круглую форму так, чтобы она больше не была симметричной между [латексом] x [/ латексом] и [латексом] y [/ латексом]. Для этого мы вводим коэффициент масштабирования в одну или обе координаты
[латекс] x [/ латекс] — [латекс] y [/ латекс]. Давайте начнем с деления всех координат [latex] x [/ latex] на коэффициент [latex] a [/ latex] и, следовательно, масштабирования значений [latex] x [/ latex]. Мы просто подставляем [latex] \ displaystyle {\ frac {x} {a}} [/ latex] в уравнение вместо [latex] x [/ latex].2 = 1 [/ латекс].
Каждое значение [latex] x [/ latex], которое решало старое уравнение, теперь должно быть умножено на [latex] a [/ latex], чтобы решить новое уравнение. Это приводит к растягиванию эллипса дальше по оси [latex] x [/ latex], потому что теперь решениями являются большие значения [latex] x [/ latex].
Точно так же мы можем масштабировать все значения [latex] y [/ latex] на коэффициент [latex] b [/ latex] (мы также предполагаем, что [latex] b> 1 [/ latex]). 2 = 1} [/ latex]
Теперь все значения [latex] y [/ latex] растянуты по вертикали, дальше от начала координат.2} = 1} [/ latex]
, что в точности соответствует уравнению горизонтального эллипса с центром в начале координат.
Если бы мы использовали коэффициенты масштабирования меньше единицы, форма сжалась бы вместо того, чтобы растягивать ее дальше.
Части эллипса
Эллипсы — это один из видов конических сечений. Особенности эллипса можно определить из его уравнения.
Задачи обучения
Обсудите, как уравнение эллипса описывает его свойства
Основные выводы
Ключевые моменты
- Эллипс образован плоскостью, пересекающей конус под углом к его основанию.
- У всех эллипсов есть две точки фокусировки. Сумма расстояний от каждой точки эллипса до двух фокусов является постоянной величиной.
- У всех эллипсов есть центр, большая и малая оси.
- Все эллипсы имеют значения эксцентриситета больше или равные нулю и меньше единицы. 2} = 1} [/ латекс ]
  , если эллипс ориентирован вертикально.Мы будем использовать горизонтальный случай, чтобы продемонстрировать, как определить свойства эллипса из его уравнения, так что [latex] a [/ latex] связан с координатами x, а [latex] b [/ latex] — с координатами y. . Для вертикального эллипса связь обратная.
  Схема эллипса: На этой схеме горизонтального эллипса показан сам эллипс красным цветом, центр [латекс] C [/ латекс] в начале координат, фокусные точки в [латексе] \ left (+ f, 0 \ right) [/ latex] и [latex] \ left (-f, 0 \ right) [/ latex], вершины главной оси в [latex] \ left (+ a, 0 \ right) [/ latex] и [latex ] \ left (-a, 0 \ right) [/ latex], вершины малой оси в [latex] \ left (0, + b \ right) [/ latex] и [latex] \ left (0, -b \ справа) [/ латекс].Он также показывает, как сумма расстояний от любой точки эллипса до двух фокусов является постоянной на [латексе] 2а [/ латексе] (длина большой оси), и как эксцентриситет определяется соотношением расстояние от точки эллипса до одного из фокусов до перпендикулярного расстояния от точки до линии [латекс] D [/ латекс], называемой директрисой, вне эллипса и перпендикулярно главной оси.
  Части эллипса
  Центр
  Центр эллипса имеет координаты [латекс] (h, k) [/ латекс].
  Основная ось
  Большая ось эллипса — это наибольшая ширина по его ширине. Для горизонтального эллипса эта ось параллельна оси [latex] x [/ latex]. Большая ось имеет длину [латекс] 2а [/ латекс]. Его конечными точками являются вершины большой оси с координатами [latex] (h \ pm a, k) [/ latex].
  Малая ось
  Малая ось эллипса — это наименьшая ширина по его ширине. Для горизонтального эллипса он параллелен оси [latex] y [/ latex]. Малая ось имеет длину [латекс] 2b [/ латекс].2 [/ латекс]
  Эксцентриситет
  Все конические секции имеют значение эксцентриситета, обозначаемое [латекс] е [/ латекс]. Все эллипсы имеют эксцентриситет в диапазоне [латекс] 0 \ leq e <1 [/ латекс]. Нулевой эксцентриситет - это частный случай, когда эллипс превращается в круг. Эксцентриситет [латекса] 1 [/ латекса] - это парабола, а не эллипс.
  Эксцентриситет определяется как:
  [латекс] \ displaystyle {e = \ frac {c} {a}} [/ latex]
  или, что эквивалентно:
  [латекс] \ displaystyle {\ begin {align} e & = \ frac {\ sqrt {a ^ 2 — b ^ 2}} {a} \\ & = \ sqrt {\ frac {a ^ 2 — b ^ 2 } {a ^ 2}} \\ & = \ sqrt {1 — \ frac {b ^ 2} {a ^ 2}} \ end {align}} [/ latex]
  Орбиты планет и их спутников представляют собой эллипсы с очень малым эксцентриситетом, то есть почти круглые. 2 [/ latex], где [latex] r [/ латекс] — это радиус, а [латекс] \ left (h, k \ right) [/ latex] — координата центральной точки.2} = 1} [/ latex], где [latex] \ left (h, k \ right) [/ latex] — координата центральной точки, [latex] 2a [/ latex] — длина большой / малой оси , а [латекс] 2b [/ латекс] — длина малой / большой оси.
- Если [latex] a> b [/ latex], большая ось параллельна оси [latex] x [/ latex]. Если [latex] a
- Чтобы определить параметры круга или эллипса, необходимо сначала привести уравнение в стандартную форму.
Ключевые термины
- эллипс : замкнутая кривая, геометрическое место точки, такое, что сумма расстояний от этой точки до двух других фиксированных точек (называемых фокусами эллипса) постоянна; эквивалентно, коническое сечение, которое является пересечением конуса с плоскостью, которая не пересекает основание конуса.
- круг : Двумерная геометрическая фигура, состоящая из множества всех тех точек на плоскости, которые одинаково удалены от другой точки.
Круги повсюду вокруг вас в повседневной жизни, от шин на машинах до пуговиц на пальто, а также на крышках мисок, стаканов и бутылок с водой. Эллипсы встречаются реже. Одним из примеров являются орбиты планет, но вы должны уметь найти площадь круга или эллипса или длину окружности на основе информации, предоставленной вам в задаче. Круги и эллипсы являются примерами конических сечений, которые представляют собой кривые, образованные пересечением плоскости с конусом.
Ниже показаны некоторые примеры проблем с разработанными решениями.
Упражнение 1
Допустим, вы садовник и только что посадили много цветов, которые хотите полить. Клумба имеет ширину 15 футов и длину 15 футов. Вы используете круговую спринклерную систему, и вода достигает 6 футов от центра. Спринклер расположен от нижнего левого угла кровати на высоте 7 футов и 6 футов выше.
1. Если бы клумба представляла собой график с левым нижним углом в начале координат, каким было бы уравнение круга?
2. Какую площадь поливает спринклер?
3. Какой процент площади сада поливается?
Ответ
Если нижний левый угол является началом координат, он имеет координаты [latex] \ left (0,0 \ right) [/ latex].2 \\ & = 36 \ pi \ end {align}} [/ latex]
Первый шаг к определению процентной доли поливаемого сада — это проверить, не падает ли вода за пределы сада. Спринклер находится в координате [латекс] \ влево (6,7 \ вправо) [/ латекс], а радиус разбрызгивателя составляет 6 футов. Вы можете проверить, не падает ли вода за пределы сада [латекс] 15 \ раз 15 [/ латекс].
Как только мы узнаем, что поливаемая площадь полностью находится внутри сада, процент поливаемой площади сада можно определить, разделив поливную площадь на общую площадь сада, а затем умножив на [латекс] 100 \%. [/ латекс]:
[латекс] \ displaystyle {\ begin {align} Percentage_ {watered} & = \ frac {A_ {sprinkler}} {A_ {цветочная клумба}} \ cdot 100 \% \\ & = \ frac {36 \ pi} { 15 ^ 2} \ cdot 100 \% \\ & = \ frac {113.
No related posts.

16.01.197012.06.2021