Математический рок — Википедия

Математический рок
Направление	Экспериментальная музыка
Истоки	нойз-рок, инди-рок, постхардкор, минимализм, постпанк, прогрессивный рок, авангардный джаз
Место и время возникновения	Конец 1980-х, США, Чикаго, Питсбург, Сан-Диего, Япония
Инструментальный рок, построк
Маткор, мат-метал, мидвест-эмо

Математический рок (англ. Math rock) — направление рок-музыки, возникшее в конце 1980-х годов в США. Математический рок характеризуется сложной, нетипичной ритмической структурой и динамикой, резкими, часто негармоничными риффами.

В рок-музыке наиболее распространен музыкальный размер 4/4. В мат-роке чаще всего используются нетипичные размеры, такие как 7/8, 11/8, или 13/8, или музыкальный размер регулярно меняется на протяжении композиции. Ритмическая сложность, казавшаяся «математической» многим слушателям и музыкальным критикам, дала формировавшемуся стилю его название. Музыку групп, исполняющих математический рок, можно отнести к построку, прогрессивному року, хэви-металу и панк-року, но эти группы никогда не могут быть отнесены к типичным представителям этих стилей.

Тексты песен и их исполнение обычно не занимают центральное место в мат-роке. Голос вокалиста обычно используется лишь как ещё один звуковой эффект или инструмент в музыкальной композиции. Кроме того, многие группы, относящиеся к этому стилю, исполняют полностью инструментальную музыку.

В то время когда некоторые музыкальные коллективы, которые возникли в 1960-х, — такие как Henry Cow, Captain Beefheart, Frank Zappa и многие другие группы 1970-х и 1980-х годов: Genesis, Gentle Giant, Rush, King Crimson,и Pink Floyd, — экспериментировали с необычными размерами, их обычно относили к определённому стилю, называемому прогрессив-рок. На канадскую панк-рок-группу NoMeansNo (основана в 1979 году) ссылаются как на оказавшую огромное «скрытое влияние» на мат-рок. Некоторые фанаты считают, что NoMeansNo — первая в истории настоящая мат-рок-группа.

В 1990-е годы более тяжёлый и структурно-сложный стиль, называемый мат-роком, выделился из нойз-рока. Этот стиль был особенно актуален в Чикаго и других городах Среднего Запада, возросший также под влиянием групп из Японии и Южной Калифорнии. Эти коллективы наследовали различные направления в музыке, начиная от Игоря Стравинского, Джона Кейджа, Стива Райха до хаотичной джазовой манеры Джона Зорна и Naked City, и критики сразу же окрестили этот стиль

мат-роком.

Группы Среднего Запада[править | править код]

В течение 1990-х годов в основном все мат-рок-группы сосредотачивались в городских центрах Американского среднего запада, в регионе, называемом Rust Belt («пояс ржавчины» или «ржавая зона»), который располагается от Миннеаполиса до Буффало с центром в Чикаго. Там же работал инженер-звукорежиссёр Стив Альбини (Steve Albini), который являлся ключевой фигурой на этой сцене. Многие мат-рок-группы поблизости привлекали его для записи своих альбомов, создавая фонотеку этого жанра, некое определённое единообразие звука и, охватывая творчество его прошлых и настоящих групп Shellac, Rapeman и Big Black, «клали их под стекло» как образец.

Также многие мат-рок-группы выпускали свои альбомы на чикагском лейбле Touch and Go Records, а также на Quarterstick Records и Skin Graft Records.

Некоторые ключевые группы того периода: Bastro, Table, Cheer-Accident, Shellac и Breadwinner. Также близ Чикаго в городе ДэКалб штат Иллинойс работала группа U.S.Maple, которая была сформирована из пепла Jesus-Lizard-подобной группы Shorty. U.S Maple были более неконструктивны в подходах создания рок-музыки, и этим походили на Captain Beefheart. Их отличало свободное обращение с ритмикой, которая в композициях только изредка возвращалась к традиционным рок размерам. Таким образом, группа не была в той же степени «математичной», как другие команды в жанре, но тот же процесс развенчивания рок-музыки по-прежнему имел место.

Несколько других мат-рок групп 1990-х, характерных экстремальной ритмической сложностью и брутальным звуком, базировалось в центральном регионе запада США: Craw и Keelhaul из Кливленда, Dazzling Killmen (Сент-Луис), Colossamite (Миннеаполис).

Питтсбургские группы[править | править код]

Город Питтсбург — родной дом для наиболее показательной мат-рок-группы Don Caballero. Образованные в 1991 году Don Caballero были всеобщими любимцами, впервые сумевшие успешно смешать тяжёлый нойз-роковый звук с влиянием авангардного джаза и неистовую игру на барабанах

Деймона Че (Damon Che). Как и многие другие группы в этом стиле, группа презирала ярлык мат-рока, который частенько приклеивали к ним критики. Пускай даже так, но ни для кого не было сюрпризом то, что временный басист Мэтт Дженсик (Matt Jencik) участник другой команды из Питсбурга, называемой Hurl, также проводил время в Don Caballero. Бывший гитарист группы Майк Бэнфилд (Mike Banfield) отмечал, что творчество коллектива Breadwinner оказало важное влияние на звучание группы. Другой бывший гитарист Don Caballero Иэн Вильямс

(Ian Williams) всерьёз «тащился» от минимализма Стивена Райха, что особенно заметно на последнем релизе группы American Don. Вильямс в дальнейшем продвигал такую манеру игры в его новом коллективе Battles. Don Caballero распались в 2001 году после происшествия с багажным фургоном группы, которое внезапно закончило их тур в поддержку альбома American Don. Несмотря ни на что Че (Damon Che) восстановил группу в 2004 году с совершенно другим составом, состоящим из участников другой мат-рок группы из Питсбурга Creta Bourzia.

В стороне от Don Caballero другие существующие группы в течение середины 1990-х годов — зенита мат-рока, такие как Shale, Jumbo и Six Horse (в которой играл один из бывших Басистов Don Caballero

Пэт Моррис (Pat Morris)), были, в общем, сходны с их местными союзниками в звуке — «математичном», металлическом роке.

Группы Сан-Диего[править | править код]

Образованная в 1990 году в Сан-Диего группа Drive Like Jehu, выделяющаяся беспорядочной гитарой Джона Райза (John Reis) из Rockets from the Crypt была блестящим примером техничной рок-музыки, которая была в лучшем виде продемонстрирована на «лебединой песне» группы, альбоме Yank Crime. Группа распалась в 1994 году.

Другие группы Сан-Диего того времени были чем-то похожи на Drive Like Jehu, среди них Antioch Arrow, Clikitat Ikatowi и Heavy Vegetable.

Последняя из списка, группа Heavy Vegetable взяла более мелодичный курс, чем две предыдущие и отличалась своим гениальным сочинителем

Робом Кроу (Rob Crow), который был в состоянии умело сплавить мелодию и гармонию со сложной ритмической структурой.

Японские группы[править | править код]

Некоторые мат-рок группы из Японии разработали тесные отношения с чикагским лейблом Skin Graft, проводя перекрестное опыление между мат-рок сценами двух наций. Наиболее важными японскими группами были Zeni Geva и Ruins, вместе с Yona-Kit, которая появилась в ходе сотрудничества японских и американских музыкантов. Интересно отметить, что японский мат-рок оказал раннее влияние на некоторые (если не на большинство) ранних американских мат-рок групп, так, например, и Zeni Geva, и Ruins образовались за несколько лет до того, как активировались их североамериканские коллеги.

Вашингтонские группы[править | править код]

Вашингтон так же поспособствовал в образовании звука мат-рока, такими группами как Shudder to Think, Faraquet, 1.6 Band, AutoClave, позже Jawbox и Circus Lupus, а также другие. Позднее говорилось о влиянии звука ранних Q and not U. Несмотря на то, что у вашингтонских групп была тенденция включать необычные размеры в свои уже эклектичные замесы, некоторые из них были отнесены к этому жанру.

Группа из Ричмонда Breadwinner, которых случайным образом приписывают в нишу мат-рока, рассматривая только их раннее творчество, породила некоторое количество более поздних групп в этом же городе. В общем, в прямые потомки можно включить Sliang Laos и Ladyfinger, а в качестве предшественников можно назвать Honor Role и Butterglove. Хотя существовали и другие Ричмондские группы связанные с жанром мат-рок, такие как Kenmores, Sordid Doctrine, MEN, Alter Natives, Mao Tse Helen, Hose.got.cable, Mulch, Hegoat, King Sour, chutney, HRM, Nudibranch, Gore de Vol и Human Thurma. Недавно образованная группа Hex Machine в своём роде продолжают эту связь с влиянием мат-рока, и эта связь охватывает участников Human thurma, Discordance axis и Sliang Laos. Кроме того, Ричмондские Lamb of God относят Breadwinner к ранним основным источникам вдохновения.

Звук Луисвиля[править | править код]

В 1991 году Slint — молодая команда из Луисвиля — выпустила свой альбом Spiderland. Он задумывался, как крайне влиятельный по своей значимости альбом, но не только для мат-рок сцены, но и вообще для всей андеграундной музыкальной аудитории внутри и снаружи. Звук этой недолго существующей группы, базирующийся на соединении множества гитарных партий, записанных на чистом «звуке» (не перегруженном) в сложном ритмическом размере, был более спокойным, уравновешенным и не таким металлизированным, как у большинства других мат-рок групп. Таким образом этот стиль (и его клоны) представляли отдельную ветвь в жанре мат-рока. Несколько групп, которые последовали в своём творчестве за Slint (включая те, в которых впоследствии играли её бывшие участники) так же использовали нестандартные размеры. Такими группами были Bitch Magnet, Rodan, Crain, The For Carnation, June of 44, Sonora Pine, Roadside Monument и Shipping News.

Vanguarda Paulista[править | править код]

В ранние 1980-е город Сан-Паулу дал толчок для движения, которое называлось Vanguarda Paulista. Оно процветало в крупнейших южно-американских городах в те времена, когда начала сыпаться бразильская военная диктатура. В оригинале Vaguarda Paulista было авангардным крылом популярной бразильской музыки (MPB) завоёванной такими артистами как Arrigo Barnabé, Alice Ruiz, Hélio Ziskind, Patife Band и многими другими, кто играл угловатый джаз-рок, с постоянно «скачущими» размерами, вызывающий ассоциации с Фрэнком Заппой (Frank Zappa) и Генри Кау (Henry Cow). К началу XXI века появилась Новая Волна арт-рок групп таких как: Hurtmold, Objeto Amarelo и Retórica, которые были под сильным влиянием звука Северного полушария, что и сделало упоминание об этих группах уместным где-либо в этой статье. Новые Бразильские группы иногда называют Vanquarda Nova или New Vanquard.

Современный мат-рок[править | править код]

На пороге XXI века большинство групп предыдущего поколения такие, как Thumbnail и Sweep the Leg Johnny распались, и как одно из многих музыкальных движений, определяемых в постоянно изменяющейся и неуловимой андеграундной рок-сцене, мат-рок-движение перестало признаваться большинством групп, к нему относящихся.

Несмотря на это, влияние движения можно заметно проследить в творчестве авангардной и инди сцен. Настоящие команды, обозначившие себя, как мат-рок группы включают такие коллективы как Oxes из Балтимора, Yowie из Сент-Луиса, чей альбом Cryptooology полностью выдержан в нечётных, полиритмических размерах, Big Bear из Бостона и группа из Сан-Франциско Sleepytime Gorilla Museum.

Некоторые группы, относящиеся к мат-року, переживают сейчас что-то вроде второй волны популярности, путём воссоединений и выдающихся событий. Примером из недалёкого прошлого может послужить тур воссоединения группы Slint в 2005 году, воссоединение Chavez в 2006. Возобновление активности Shellac или, например, воссоединение Don Caballero с выходом их нового альбома в 2006 году выглядит именно так, как будто группы из Питсбурга продолжают сочинять сложную рок-музыку. Майк Бэнфилд (Mike Banfield) участник Don Caballero с самого первого состава собрал группу Knot Feeder в 2006, так же как и экс-басист Пэт Моррис (Pat Morris) образовал The Poison Arrows.

К тому же в разных уголках США появляются с завидным постоянством новые рок-группы, которые так или иначе используют мат-роковую концепцию для формирования собственного звука, собственных методов подачи, среди них такие как: Rumah Sakit, Tera Melos, Medications, Gastr Del Sol, We versus the Shark, Cinemechanica, Piglet, Sleeping People и многие другие коллективы.

Великобритания совсем недавно тоже начала проявлять интерес к мат-року в лице таких групп, как ¡Forward, Russia!, Secondsmile, 65daysofstatic, Maybeshewill и Youthmovie Soundtrack Strategies. Хотя эти группы нельзя назвать типичными мат-рок-командами, но невозможно не заметить огромное влияние этого жанра на творчество этих коллективов.

Наиболее близким жанром по отношению к мат-року приходится построк, к которому отчасти можно отнести некоторые из выше описанных групп. Хотя построк обычно стремятся определить, как более гладкую, мелодичную, более гармоничную рок-музыку.

ru.wikipedia.org

Музыка Math rock | Last.fm

Теги

Связано с:

Математический рок (реже — мат-рок, англ. Math rock) — направление рок-музыки возникшее в конце 80-х гг. в США. Математический рок характеризуется сложной, нетипичной ритмической структурой и динамикой, резкими, часто негармоничными риффами. В рок-музыке наиболее распространен музыкальный размер 4/4. В мат-роке чаще всего используются нетипичные размеры, такие как 7/8, 11/8, или 13/8, или музыкальный размер регулярно меняется на протяжении композиции. Ритмическая сложность, казавшаяся «математической» многим слушателям и музыкальным критикам, дала формировавшемуся стилю его название… подробнее Математический рок (реже — мат-рок, англ. Math rock) — направление рок-музыки возникшее в конце 80-х гг. в США. Математический рок характеризуется сложной, нетипичной ритмической структурой и динамикой, резкими, часто негармоничн… подробнее Математический рок (реже — мат-рок, англ. Math rock) — направление рок-музыки возникшее в конце 80-х гг. в США. Математический рок характеризуется сложной, нетипичной ритмической структурой и динамикой, резкими, часто негармоничными риффами. В рок-музыке наиболее распространен музыкал… подробнее

1. 
2. 

   Foals

   1 499 229 слушателей

3. 

   Battles

   543 805 слушателей

4. 
5. 

   Slint

   295 830 слушателей

6. 
7. 

   Hella

   163 217 слушателей

8. 

   Shellac

   164 157 слушателей

9. 
10. 

Другие исполнители

www.last.fm

МАТЕМАТИКА + МУЗЫКА = УСПЕХ

МАТЕМАТИКА + МУЗЫКА = УСПЕХ

Пересецкая В.И. 1

---

1МОУ ИТЛ №24 им. Е.А. Варшавского

Лаптева Т.П. 1

---

1МОУ ИТЛ №24 им. Е.А. Варшавского

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Я учусь в 5 «А» классе лицея №24. Мне нравятся многие школьные предметы, но одним из самых интересных, хоть многим и нелегко дающихся, является математика – царица всех наук. Как же здорово иногда поломать голову над задачками и головоломками! Математические знания для меня нужны и важны, так как я собираюсь продолжить обучение в нашем лицее.

А ещё я учусь в музыкальной школе, и музыка – это моё самое любимое увлечение. Порой мне кажется, что она каким — то образом помогает мне в изучении математики, и наоборот, математика помогает мне быстрее и успешнее развиваться в музыке.

Какая связь может быть между математикой, мудрой царицей всех наук, и музыкой? И сегодня в моей работе, я предлагаю вам найти ответы на эти вопросы.

Если вспомнить слова знакомой всем песенки:

Дважды два – четыре,

Дважды два – четыре,

А не три, а не пять,

Это надо знать! ….

(сл. М. Пляцковского),

то с помощью её можно легко запомнить некоторую часть таблицы умножения. Может занятия музыкой помогают изучению математики?

Так возникла тема моего исследования: «Математика + музыка = успех».

Целью моей работы является доказательства того, что математика и музыка тесно связаны, в них есть очень много общего. И если «математика ум в порядок приводит», то музыка воспитывает уважение к числу, формирует нравственные качества человека, помогает более тонко чувствовать окружающий мир.

Задачи, которые я поставила перед собой, это:

• найти общие понятия для музыки и математики;

• проанализировать запись музыкального произведения;

• провести исследование по установлению связи между музыкой и математикой, рассмотрев музыкальное произведение, как математическую модель.

Я выдвинула гипотезу, что любое музыкальное произведение можно представить в виде математической модели.

В ходе работы использовала следующие методы исследования: поисковый, сравнение, анализ, обобщение.

Актуальность темы. На сегодняшний день музыка и математика – родные сёстры, они созданы и помогают друг другу. Приучают к дисциплине, развивают эрудицию, творческие способности, внимание.

1. Основная часть

1.  

   1. История связи музыки и математики

Музыка существует на земле тысячи лет. Изобретение музыки нельзя приписать никому так же, как нельзя приписать кому-либо изобретение человеческой речи. Еще в древности было сложено множество интересных легенд о том, как возникла музыка. Древние греки считали её великим даром богов. Бог Аполлон был у них покровителем искусства, и особенно музыки. Его обычно изображали с музыкальным инструментом в руках.

При первобытном строе, музыка играла очень важную роль. Матери, напевая, укачивали детей, воины устрашали врагов воинственными песнями – кличами, пастухи протяжными зовами собирали стада. Если из племени кто-то умирал, то его провожали песней-плачем.

В своих трудах учёные неоднократно делали попытки представить музыку, как некую математическую модель.

Одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор⁽²⁾.

Он создал свою школу мудрости, положив в её основу два предмета — музыку и математику.

Пифагор считал, что гармония чисел сродни гармонии звуков и что оба

этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он придумал гамму из восьми звуков – это самая древняя музыкальная гамма. Взятая за основу Пифагорова гамма, в дальнейшем усовершенствовалась появился темперированный строй, состоящий из 12 нот, включая диезы и бемоли.

Нужно отметить, что ученики Пифагора проводили занятия математикой под музыку, так как заметили, что она благотворно влияет на ум.

Позже в своих трудах учёные неоднократно делали попытки представить музыку как некую математическую модель. Примером этого служит цитата из работы Леонарда Эйлера «Диссертация о звуке», написанная в 1727 году. «Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований всё, что может сделать приятным объединение и смешивание звуков».

Лейбниц в письме Гольдбаху пишет: «Музыка есть скрытое арифметическое упражнение души, не умеющей считать». На что Гольдбах ему отвечает: «Музыка — это проявление скрытой математики».

1.  

   1. Средневековое понимание цифр в музыке

При знакомстве с музыкальной эстетикой средневековья необходимо иметь в виду, что в то время музыка понималась не как искусство, a как наука.

Известно, что музыка входила в состав семи «свободных искусств», делившихся на «trivium» (грамматика, риторика, логика) и «quadrivium» (арифметика, геометрия, астрономия, музыка). Характерно, что музыка относилась именно к сфере математических знаний. Тем самым она признавалась одной из математических дисциплин, одной из отраслей математики. И как таковая она понималась, прежде всего, как наука о числах.

В IV-V веках в странах Западной Европы появляется обширная литература на латинском языке, посвященная теоретическим вопросам музыки. В это же время появляется трактат Августина⁽⁵⁾ «О музыке», состоящий из шести книг, а в 430 году — книга Марциана Капеллы «О музыке». В период с 500 по 510 год пишет свои пять книг о музыке Боэций.

1.  

   1. Общие элементы в математике и музыке

На первых уроках сольфеджио – это уроки музыкальной грамоты, ученики музыкальных школ сразу же сталкиваются с математикой.

В музыке всёсчитать надо, как и в математике:

• 7 нот,

• 5 линеек нотного стана,

• интервалы, аккорды.

Символы в математике и в музыке неотделимы. В математике мы используем цифры, знаки действий и т.д., а в музыке ноты, с помощью которых создаётся музыка.

1.  
   1.  

      1. Ритм

Окружающий нас мир полон ритмов. О чём говорит это слово?

Оглянитесь вокруг. Прислушайтесь. Ритмично звучат шаги: раз-два, левой – правой, ритмично наше дыхание, ритмично тиканье часов или стук колес проходящего поезда. Поэтому с ритмами мы встречаемся на каждом шагу в повседневной жизни: день сменяется ночью, зима – весной и т.д.

А в музыке ритм – это чередование долгих и коротких, одинаковых и разных по длительности звуков:

Ритм⁽¹⁾ – основа всего музыкального движения, порядок сочетания во времени всех элементов музыкальной речи: мелодии, гармонии и т.д.

В музыкальном произведении ритм обозначается цифрами, которые называются размером. Рассмотрим размер 3/4 и 2/4.

От правильно подобранного ритма зависит звучание мелодии.

Математика также заимствовала данное слово. Ритмы можно обнаружить и среди чисел. Вспомним ряд натуральных чисел: 1, 2, 3, 4, 5,… Ощущаете ритм? Его основа – каждое последующее число получается из предыдущего, если к нему прибавить единицу. В математике такая последовательность чисел называется арифметической прогрессией.

1.  
   1.  

      1. Длительность

При записи мелодии, звуки имеют свою длину (длительность⁽¹⁾).

Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби.

Принцип построения длительностей соответствует принципу построения бесконечной убывающей геометрической прогрессии. И если записать длительности от «целой» ноты, (которая принята в музыке за единицу) по степени убывания, то получим: Каждый член прогрессии уменьшается в два раза.

Каждый ряд этой «нотной пирамиды» равен четырём долям. Это как пирог делится на 8 частей, так и целая нота делится на восемь восьмых.

Самая “длинная” нота – целая, если нажать клавишу пианино и начать про себя считать, то эта нота будет тянуться: раз – и – два – и – три – и – четыре – и.

С точки зрения математики целую ноту можно принять за единицу (1).

Нота вдвое короче называется половинной, она тянется: раз – и – два – и. Половинной ноте соответствует дробь .

В два раза короче половинной ноты – четвертная нота. Она тянется: раз – и. Ей соответствует дробь .

Восьмая нота тянется на раз или и — .

Шестнадцатая нота: на раз или и звучат две ноты — .

На основе этого можно построить математическую модель:

1 = = = =

Как мы видим, звуки тянутся неодинаково: есть звуки, которые длятся очень коротко, как будто строчит пулемёт, а есть звуки, которые, наоборот, тянутся очень долго – это часто бывает в конце песен. Вот для того, чтобы музыкант знал, сколько должна тянуться каждая нота, и решили по-разному обозначать длительности нот.

Иногда в процессе обучения музыке возникают небольшие трудности, и одной из них является счёт, то есть пока разучиваю новую, незнакомую пьесу, я должна вслух или про себя считать, чтобы понять мелодию.

Всякое музыкальное произведение состоит из тактов, разделённых вертикальными линиями.

Представьте себе лестницу в подъезде. Каждый пролёт её считаем тактом, каждую ступеньку – нотой или аккордом. Собственно размером, принято считать количество ступенек в каждом пролёте. Довольно просто, не так ли? Будучи основой музыкального ритма, размер содержит одинаковое количество нот-ступенек определенной длительности в каждом такте-пролете. Музыкальный размер указывается в начале произведения.

Размер 4/4 (четыре четверти) является самым простым и, одновременно, самым популярным во всех направлениях музыки. Две четверки означают, что длительность каждого такта равна длительности звучания четырёх четвертных нот. Как отсчитывать ритм, спросите вы? Ровными ударами в темпе конкретного музыкального произведения. В данном случае по четыре удара, например ногой по полу, на каждый такт.

1.  
   1.  

      1. Параллели

В музыке, как и в математике, тоже есть понятие параллельности.

Прежде всего – это пять параллельных прямых, которые образуют нотный стан, на котором размещаются ноты, выше или ниже по отношению друг к другу. Этим они отличаются по звучанию. Измерить высоту нот как раз и помогают параллельные линейки.

В жизни мы часто наблюдаем параллельность – это рельсы, строки в книгах, капли дождя, брусья в гимнастике.

В музыке параллельные линии можно увидеть не только в нотах, но и во внешней форме некоторых музыкальных инструментов: струны арф или органные трубы.

Параллели можно обнаружить в самом звучании музыки. Сравните, что получится, если одна и та же мелодия будет исполнена различными голосами, то есть одновременно, в унисон будут петь 2 голоса. Например, женский голос будет звучать в верхнем регистре, а мужской – в нижнем.

Параллельно могут звучать голос и фортепианное сопровождение или какой-нибудь музыкальный инструмент (скрипка, флейта, виолончель) с фортепианным сопровождением.

Параллельно будут звучать голоса туристов при исполнении песен у костра, а может, и в хоре при условии исполнения произведений в унисон.

1.  
   1.  

      1. Противоположности

Весь мир состоит из противоположностей.

В математике существуют множество противоположностей:

• плюс – минус;

• прямая – кривая;

• чётное число – нечётное число;

• больше – меньше;

• сложение – вычитание

• тупой и острый.

• быстро – медленно;

• громко – тихо;

• короткое – длинное;

• одноголосие – многоголосие;

• вокальная музыка – инструментальная музыка.

• Пара медленно – быстро играет весьма важную роль в музыке. Характер песни во многом определяется её темпом. И искажая темп, можно исказить и всё произведение.

• Высокое – низкое. Это в большей степени относится к музыкальным инструментам. Высоким звучанием отличаются, например, флейта – пикколо, скрипка; низким – контрафагот, туба, контрабас.

1.  
   1.  

      1. Симметрия в музыке

• В музыке часто используется симметрия⁽⁶⁾. Ряд музыкальных форм строятся симметрично. В этом отношении особенно характерно рондо (от французского — круг). В рондо музыкальная тема многократно повторяется, чередуясь эпизодами различного содержания. Главная тема проводится не менее трех раз в основной тональности, а эпизоды – в других тональностях. Это напоминает зеркальную симметрию, основная тема служит плоскостью, от которой как бы отражаются эпизоды. Но тот эпизод, который раньше прозвучал в высокой тональности, повторяется в низкой, и наоборот.

• Простейшее – симметрия нотного стана.

• Виды симметрии:

• ракоходное отражение – зеркальный вид симметрии в геометрии. Отражённые ноты кажутся такими, какими они действительно выглядели бы в зеркале.

• Обращение исходит из звуковой последовательности, которая испытывает

• зеркальное отражение в плоскости.

• ракоходное обращение – это когда в зеркальной части снова меняется направленность звукового ряда по высоте.

• трансляционный вид – это самый распространённый вид симметрии в музыке. В этом случае музыкальная фраза повторяется, оставаясь неизменной. Но в

• некоторых случаях возможна асимметрия, то есть отступление от оригинала, для красоты звучания.

• Многократное повторение небольшого мотива из разных ступеней лада, как в восходящем, так и в нисходящем направлении.

• ракоходное обращение с зеркальным отражением – поворотно-зеркальный вид в геометрии. Нотный лист можно повернуть на 180°, но мелодия останется неизменной.

1.  
   1.  

      1. Интервалы

• Музыкальный интервал⁽⁵⁾ — это расстояние по высоте между двумя звуками. Данное слово происходит от латинского intervallum – промежуток, расстояние.

• Название интервалов в переводе на русский язык означает число.

• Прима – один

• Секунда – два

• Терция – три

• Кварта – четыре

• Квинта – пять

• Секста – шесть

• Септима – семь

• Октава – восемь

• Нона – девять

• Децима – десять

• Ундецима – одиннадцать

• Терцдецима – двенадцать

• Квартдецима – четырнадцать

• Квинтдецима – пятнадцать

• Расстояние между звуками в музыке измеряется полутонами.Полутон – то ближайшее расстояние между двумя звуками, то есть два соседних звука.

• Размеры интервалов до октавы:

• Прима (ч1) = 0 тонов

• Малая секунда (м2) = пол тона

• Большая секунда (б2) = 1 тон

• Малая терция (мЗ) = 1,5 тона

• Большая терция (б3) = 2 тона

• Кварта (ч4) = 2,5 тона

• Тритон (ув4 или ум5) = 3 т

• Квинта (ч5) = 3,5 тона

• Малая секста (м6) = 4 тона

• Большая секста (б6) = 4,5 тона

• Малая септима (м7) = 5 тонов

• Большая септима (б7) = 5,5

• Октава (ч8) = 6 тонов

• Интервалы бывают большие(б), малые(м), чистые(ч), увеличенные(ув), уменьшённые(ум).

• Все интервалы взаимообратимы. Например, если написать секунду и перевернуть её на 180 градусов, получится септима. И так будет с каждым интервалом: прима-октава – секунда-септима, терция-секста – кварта-квинта.

1.  
   1.  

      1. Вариации

• Что такое вариации? Форма музыкального произведения, состоящего из нескольких частей, каждая из которой звучит с изменениями. Существуют 3 типа вариаций: мелодические, ритмические, гармонические. Композитор, разрабатывая избранную им тему, может варьировать её мелодический рисунок, видоизменять ритм и гармонию, т.е. созвучия. Разумеется, он может варьировать одновременно 2 или даже 3 элемента, с каждой вариацией все, более уходя от начальной темы.

• Число можно определить и описать многими способами. Числа тоже можно задавать словами, иногда это даже удобнее, чем обычная цифровая запись и наоборот. 15 = 10 + 5 = 25 – 10 = = и т.д.

1. Практическая часть

• Провести исследование связи между музыкой и математикой я решила на примере украинской народной песни «Два весёлых гуся».

• Проанализировав запись этого музыкального произведения, я заметила, что первая музыкальная фраза, состоящая из одного такта, повторяется два раза подряд. В третьем такте присутствует один из видов симметрии – секвенция – разновидность трансляционного вида симметрии, а также и сам трансляционный вид. Третий и четвёртый такты, как припев песни, повторяется также два раза. Размер произведения – .

• ДВА ВЕСЁЛЫХ ГУСЯ

• Украинская народная песня

• Для записи песни «Два весёлых гуся» на математическом языке под каждой нотой песни я подписала дробь, значение которой соответствует длительности ноты. Складывая дроби, проверила, что их сумма в каждом такте равна заданному ритму – .

• Запись песни с помощью дробей можно рассматривать как математическую модель музыкального произведения.

• + + + + + + + + + +

• + +

• + +

• + + + + + + + + + + + +

• +

• +

1. Заключение

• Выполняя работу, я убедилась, что музыка и математика тесно связаны друг с другом, в них есть много общего. Общие понятия — параллели, противоположности, симметрия построения. Существуют общие черты в использовании специальных символов для записи числа – цифры, а в музыке – ноты, целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби. Можно уверенно сделать вывод о том, что, не зная математических понятий, не умея различать дроби, не умея сравнивать их, невозможно было бы сыграть музыкальный фрагмент.

• Анализ музыкального произведения подтвердил предположение об их симметричном построении.

• Музыкальные и математические операции родственны и содержательно и психологически. Занимаясь музыкой, человек развивает и тренирует свои математические способности.

• В практической части своей работы я составила математическую модель музыкального произведения, записав его на языке дробей.

• Я считаю, что цель моей работы достигнута, задачи выполнены, гипотеза доказана. Изучение данной темы, на мой взгляд, может быть продолжено, так как литературы о связи музыки и математики очень мало.

• Сравнивая музыку и математику, я сделала вывод, что математика, как наука может развиваться без музыки, а музыкальное искусство подчиняется многим законам математики и не может существовать без неё. «Музыка есть таинственная арифметика души; она вычисляет, сама того не сознавая».

1. Литература

1. Вахромеев В. /Элементарная теория музыки/. – М.: Наука, 1970 год.

2. Жмудь Л.Я. /Пифагор и его школа/. – М.: Наука, 1990 год.

3. Шарапкина Е.П. /Гармония математики и музыки/. – Университетские чтения, 2006 год.

4. http://www.px-pict.com/7/3/2/1/5.html

1. http://musicfancy.net/ru/music-theory/theory/97

1. http://uchitelya.com/music/17939-prezentaciya-simmetriya-v-muzyke-7-klass.html

13

Просмотров работы: 4595

school-science.ru

Математика и музыка Математический компонент музыкального языка.

Алиса Самбурская, к.п.н.

«Взаимосвязью между музыкой и математикой интересовались еще в древности. И это неудивительно, поскольку присутствие в музыке математического компонента очевидно. Самые важные характеристики звука – его высота и длительность – определяются количеством колебаний и продолжительностью звучания, которые в свою очередь выражаются посредством конкретного числа.

Как известно, пифагорейцы предположили, что в основе мира лежит некая абстракция – число. Более того, число в различных ипостасях: «бог-число», «вещь-число», «искусство-число» и т.д. стало у них сущностью мира. Эта числовая конструкция бытия мыслилась ими как конкретный «музыкально-числовой космос» или «строй мира», действующий гармонично во всех проявлениях. Таким образом, Пифагор и его последователи попытались объединить математику, гармонию и музыку в единую сущность не только космоса, но и человеческой души и конкретной вещи. Музыкальная гармония мыслилась древними как некая логически построенная система, которая имеет много общего с математикой. В глубокой древности было подмечено определенное соответствие между высотой звука и конкретным числом, определяющим длину струны. Именно по этому принципу был создан широко популярный в античности музыкальный инструмент – лира, который впоследствии стал эмблемой музыкальной искусства.

Рассмотрим взаимосвязи между математикой и музыкой с точки зрения ее теоретического построения. Основой математических знаний является арифметический счет. Счет, как числовой ряд, состоит из определенной последовательности чисел, в которой каждое последующее число больше предыдущего на одну единицу – и это уже само по себе является определенной ритмической закономерностью. Арифметические действия с числами происходят путем перемещения по этому числовому ряду либо в сторону увеличения, либо наоборот. Чтобы, например, к двум прибавить пять, нужно от 2 переместиться на 5 единиц в сторону увеличения чисел – получаем 7. По аналогии, музыкальный звукоряд – это последовательность музыкальных звуков, в которой каждый последующий звук выше предыдущего также на одну единицу, (в музыке ей соответствует полутон), если звукоряд восходящий. Cоответственно, если звукоряд нисходящий, то каждый последующий звук ниже предыдущего на пол-тона. Аналогично арифметическому действию мы можем вычислить музыкальный звук путем перемещения по музыкальному ряду.

Ученые, изучавшие взаимосвязь между восприятием музыки и мыслительными процессами (Генрих Гетце 1994, Мария Спайхигер 2000) утверждают, что оперируя математическим рядом чисел и выполняя любые арифметические действия «в уме», будь то сложение, вычитание, умножение, деление или даже извлечение корня и возведение в степень, человек достигает результата весьма похожими пространственными мыслительными операциями, что и при дифференциации звуковысотности и длительности. Нам также кажется весьма логичным утверждение, что существует определенная связь между арифметическими и музыкальными мыслительными операциями. При написании музыкального диктанта человек, не обладающий абсолютным музыкальным слухом вполне в состоянии записать точно и правильно прослушанную им мелодию, если он хорошо дифференцирует сравнительную звуковысотность (выше-ниже), темп (быстрее-медленнее), музыкальные длительности (дольше, короче, длиннее). Способность дифференцировать эти сравнительные соотношения тренируется и развивается музыкальными занятиями. Те же соотношения используются и в математике.

Определение интервала в музыке есть не что иное как вычисление разности между двумя звуками. Интересно и то, что когда музыканты воспринимают музыкальные интервалы, то в их воображении автоматически возникает числовой ряд, отрезок которого равен определенному интервальному отрезку, т.е. представляется отрезок чисел от 1 до 4 — если слышат кварту, от 1 до 7, если септиму и т.д. Наверное, возможно также представление септимы как отрезок чисел от 2 до 9 или от 3 до 10 – он также равен 7.

Построение музыкального произведения имеет свою логику и числовые характеристики. Соотношение частей музыкального произведения образуют музыкальную форму. Составные элементы музыкальных форм – мотивы, фразы, предложения, периоды – в совокупности образуют мелодию. Обычно мотив умещается в 1-2 такта, отрезок из 2-3 мотивов образует относительно законченное музыкальное построение, называемое фразой; 2фразы образуют предложение, 2 предложения составляют законченный раздел, завершающийся кадансом и который называется периодом, который состоит в свою очередь из 8 или 16 тактов. Разные способы развития и сопоставления элементов мелодии образуют различные типы музыкальных форм. Так, последование 2 периодов образуют простую двухчастную форму, 3 раздела образуют сложную трехчастную форму. Существуют и другие музыкальные формы: тема с вариациями, куплетная форма, рондо, сонатная форма, фуга, смешанные формы. Но все они представляют собой определенную формулу музыкального построения, как, например, известная 12-тактовая формула классического блюза или формула построения джазовой пьесы.

Изучив определенные законы построения музыкального произведения, можно научиться сочинять музыку – по формуле, точно также как и формально сочинять стихи. (Правда, нет гарантии, что эти произведения будут представлять из себя какую-либо художественную ценность). И хотя композиторами становятся далеко не все студенты музыкальных отделений, тем не менее на занятиях по музыкальной гармонии фуги сочиняют все.

Что же касается нотной записи, то здесь без математических знаний не обойтись! То, с чего собственно и начинается музыка, один из основных элементов выразительности мелодии (наряду с различной высотой, интервальными соотношениями звуков, составляющих мелодию) – это ритм. Мелодия образуется только в том случае, если звуки организованы ритмически, т.е. определяются определенными длительностями. Чередование звуков вне ритма не воспринимается как мелодия; ритм же подчас настолько ярко характеризует мелодию, что ее можно узнать только по обозначению длительностей звуков без указания их высоты.

Основные ритмические измерения, применяемые в музыке — это относительные длительности: целая нота, половинная, четвертная, восьмая, шестнадцатая, тридцать вторая.

Относительной длительностью называется продолжительность данного звука по сравнению с другими. Абсолютная же длительность звуков в музыке устанавливается темпом, т.е. скоростью звучания, а именно показателем скорости по метроному. Доля такта – это единица метра музыкального размера. Доли такта представляют собой малые отрезки одинаковой длительности, из которых складывается данный текст. Величина доли такта указывается в знаменателе дроби, обозначающей размер: например, в размере 3/4 – долей такта является четвертная нота, в размере 2/2 – половинная, в размере 3/8 – восьмая. Числитель дроби указывает количество долей в такте. Показатель по метроному определяет, сколько долей (половинных, четвертных или восьмых) должно прозвучать в течение минуты.

Так, обозначение четвертная нота = 80 указывает, что в минуту должны прозвучать 80 четвертных долей (и соответственно – 40 половинных или 160 восьмых и т.д.). Причем абсолютная длительность звуков является важнейшим условием музыкальной выразительности, от которого зависит замысел музыкального произведения.

Таким образом, общность и единообразие математических и музыкально-теоретических процессов очевидно, и это служит свидетельством того, что занятия математикой могут значительно облегчить изучение музыкальной гармонии и сольфеджио, и наоборот – решение музыкальных задач и упражнений или даже просто активное восприятие музыки может способствовать улучшению арифметических навыков.

В связи с этим нам представляется весьма интересным использование музыкальных видов деятельности при обучении детей математике.

____

ГЛОССАРИЙ

Полутон – наименьшее расстояние между двумя различными по высоте звуками, «единица измерения» в музыкальной системе.

Диктант музыкальный – специальное упражнение по сольфеджио, небольшой музыкальный отрывок, предназначенный для прослушиваний, запоминания и записи нотными знаками.

Абсолютный слух – абсолютная память на высоту любого звука.

Музыкальный интервал – расстояние между двумя звуками. Если звуки взяты последовательно, то такой интервал называется мелодический, если звуки взяты одновременно – гармонический.» [сайт «Музыка интеллекта» http://alicepush.ucoz.ru/]

***

Впрочем… ?

Великий немецкий композитор Людвиг Ван Бетховен так и не смог освоить все арифметические операции. Умножение и деление были для него нераскрытой тайной. Например, чтобы умножить 12 на 60, гениальный композитор 60 раз складывал по 12. Правда и математики не оставались «в долгу» перед музыкальным искусством. Так, великому австрийскому математику Георгу Вега музыка была настолько чужда, что он говорил: «Не существует ни хорошей музыки, ни плохой. Существует лишь большой шум и малый шум». [Математический юмор. //Виртуальная школа юного математика. — http://www.math.md/school/zanimat/iumor/iumor.html]

***

И тем не менее !

studfile.net

Исследовательская работа «Математика в музыке»

Государственное автономное профессиональное образовательное учреждение

Чувашской Республики

«Чебоксарский техникум технологии питания и коммерции»

Министерства образования и молодежной политики Чувашской Республики

Математика в музыке

Выполнил:

Студент 1 курса, группа №62

Яндакова Светлана Сергеевна

Научный руководитель:

Николаева Людмила Николаевна

Чебоксары, 2017

Содержание

Введение 3-4

1. История исследования связи музыки с математикой 5-6

2. Связь между звуками и числами 7-8

3. Восприятие математики и музыки 9

4. Математическая чистота звука 10

5. Золотое сечение в музыкальных произведениях 11

6. Практическая часть 12-13

7. Музыкальные задачи 14

8. Заключение 15

9. Список использованной литературы 16

10. Приложение 1 17

Введение

Настоящая наука и настоящая музыка требуют однородного мыслительного процесса
( А. Эйнштейн )

Актуальность:

Математика и музыка — два предмета, два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.

Музыка (от греч. — искусство муз) — вид искусства, художественным материалом которого является звук, особым образом организованный во времени. Математика (от греч. – знание, наука). — наука о величинах, их свойствах и законах их соединения.

Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства. Какова роль математики в музыке? Как тесно они связаны? Возможно, законы математики добавляют красоту в те звуки, что мы слышим? Человек, увлеченный музыкой, имеющий точный слух, способности к занятиям музыкой и разбирающийся в математике, имеет больше шансов сочинить красивое музыкальное произведение, или математические закономерности появляются в музыке благодаря внутренней интуиции гениального автора? В своей работе я предлагаю найти ответы на эти вопросы, и доказать, что связь между музыкой и математикой существует.

Целью моей исследовательской работы является проведение параллели между музыкой и математикой, на основе музыкальных произведений, для выявления взаимосвязи между ними.

Задачи исследования:

• Выяснить, были ли в истории попытки связать музыку с математикой.

• Выявить общие элементы между звуками и числами;

• Провести свои исследования по выявлению математических закономерностей.

• Отыскать преимущество применения законов математики в написании музыки.

3

Объект исследования — математика и музыка.

Предмет исследования — элементы математики в музыке.

Гипотеза — любое музыкальное произведение можно представить, как некую математическую модель, которая будет иметь числовую закономерность.

Методы исследования:

• Изучение, обработка и анализ документов и интернет — источников.

• Исследование музыкального произведения .

• Метод проблемно-поисковой ситуации.

4

1. История исследования связи музыки с математикой

Математика – царица наук, тесным образом перекликается с музыкой.

Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.

В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.

Рассматривать музыку, как один из объектов математики, пытались многие величайшие математики. Исследованию музыки посвятил свой первый труд Рене Декарт («Трактат о музыке»), Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие. В своих трудах они хотели представить музыку как некую математическую модель. Леонард Эйлер («Диссертация о звуке», 1727 г.) пишет: «Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований всё, что может сделать приятным объединение и смешивание звуков». Об отношении к математике и музыке ученые высказывались в своих личных переписках. Лейбниц в письме Гольдбаху пишет: «Музыка есть скрытое арифметическое упражнение души, не умеющей считать». На что Гольдбах ему отвечает: «Музыка — это проявление скрытой математики». 

Слова мелодия, ритм родились в Элладе, название слова «гамма» происходит от греческой буквы (гамма). После создания точной математической теории струны, поняв, что любой музыкальный инструмент – всего-навсего «физико-акустический прибор», музыку уже не отделить от математики. Математическому анализу подлежат и звук, и тембр, и лад, и гармония. Пифагор создал математическую теорию музыки, слушая, как звучат медные чаши. Каждое настоящее искусство имеет свою теорию, которую можно выразить в терминах математики. Математики, начиная с Пифагора, постоянно проявляли интерес к музыке. 

Именно Пифагор был первым, кто попытался выразить красоту музыки с помощью чисел. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.

Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева.

В пифагорийской школе проводили занятия математики под музыку, так как заметили, что она благотворно влияет на интеллект. Пифагор учился музыки в Египте и сделал ее предметом науки . Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать.

2. Связь между звуками и числами

С чего начинается знакомство с музыкой? Конечно, со звуков! Но чтобы их повторить, нам придётся окунуться в мир странных кружочков, палочек, крючочков и галочек, которые все вместе и будут составлять нотную грамоту. Оказывается, любую музыку можно записать с помощью семи нот, расставляя около них музыкальные знаки (аналогично в математике: десять цифр и знаки действия с ними). Ноты и паузы бывают целые, половинные, четвертные, восьмые, шестнадцатые и т.д., их связывает между собой математическая закономерность. Музыкальное произведение записывается при помощи нот не хаотично, а весь текст делится на такты, при этом все такты одного произведения имеют один размер, который и указывается в начале любого произведения. Например : ¾ будет означать, что в каждом такте должно быть ровно три четвертных ноты. При этом четвертные ноты могут разбиваться на восьмые, шестнадцатые или паузы того же размера. Расстояние между нотами (интервалы) также имеют свои названия и соответствуют определенному количеству тонов. Аккорды, которые сопровождают и украшают музыкальное произведение, высчитываются математическим путем и состоят из интервалов. Это относительно записи и чтения музыкальных произведений, но посмотрим на музыку с другой стороны.

Всякий звук — это воспринимаемые человеческим ухом колебания среды, обычно воздуха. Источником колебаний могут быть голосовые связки певца, струна музыкального инструмента, плохо смазанная дверь и т.п. Одна из основных характеристик колебательного процесса — частота колебаний. Особенность музыкальных звуков в определенной частоте колебаний. Когда говорят о частоте колебаний, определяющей ту или иную ноту, обычно употребляют термин высота звука. Ощущение высоты — это психологическая форма восприятия частоты колебаний звучащего тела, и чем больше частота колебаний, тем выше кажется звук и наоборот. 

Человеческое ухо воспринимает звук, частота которого заключена приблизительно в интервале от 16 до 16000 Гц. В музыке используется диапазон от 16 до примерно 5000 Гц. Если считать только звуки с целым значением частоты, то получится около 5 тысяч. Между тем, концертный рояль — инструмент с огромным звуковым диапазоном — имеет всего 87 клавиш. Более того, через каждые двенадцать клавиш (семь белых и пять черных) повторяется их расположение и их названия. И очень высокие и очень низкие звуки носят одни и те же повторяющиеся имена: до, фа-диез, ля-бемоль и т.д. Постараемся понять, каким образом из всего многообразия звуков были отобраны именно те, к которым мы привыкли, и почему именно через каждые 12 клавиш повторяются названия нот. Для начала займемся измерениями. А где измерения, там вступает в свои права математика. 
Каждая нота имеет определенную частоту и эту частоту можно вычислить с помощью формулы: 

 Гц
где n — это порядковый номер ступени (на клавиатуре номер клавиши слева), начиная с «ля» субконтроктавы, отсчитывается с нуля.

Например, для нахождения частоты «ре» малой октавы n будет равно 29:

 Гц

Таким образом, для каждой ноты вычисляется его частота. Раз уж звуки различаются по высоте, то естественно задать вопрос: «Насколько один звук выше другого?». И на этот вопрос удалось ответить с помощью математических вычислений. Рассмотрим отношения нескольких пар звуков. На слух звук с частотой 97,999 Гц настолько же выше звука с частотой 65,406 Гц, насколько звук в 783,99 Гц выше звука в 523,25 Гц. Во всех случаях мы имеем: отношение для каждой пары одно и то же и равно 3/2. Таким образом, отношение частот звука любой ноты к ноте до в любой октаве одинаковое. Расстояние между нотами, определяемое отношением их частот, называется интервалом. Некоторые, наиболее важные в музыке интервалы получили свои собственные имена. Так, отношение частот 3/2 определяет интервал квинты, а интервал октавы — образуют две ноты с отношением частот 2. Две одинаковые по высоте ноты относятся друг к другу с коэффициентом 1 и образуют интервал примы. 

Интервалы имеют направление и могут определять движение как вверх, так и вниз (сравнимо с координатной прямой в математике). Переход от ноты с частотой ω к ноте с частотой 2ω дает октаву вверх, к ноте с частотой 2ω/3 — квинту вниз. 

Чем же важен интервал октавы? Пусть наш исходный звук — нота до первой октавы. Возьмем от нее октаву вверх и октаву вниз. На слух эти три звука очень похожи, практически сливаются в одно целое. Поэтому обе получившиеся ноты также называются до, только расположены они в других октавах. Таким образом, частоты любых двух одноименных нот относятся друг к другу как некоторая степень числа 2.

Математическое описание этого явления было дано значительно позже усилиями д’Аламбера, Эйлера, Даниила Бернулли, Лагранжа. Такие выдающиеся имена не оставляют сомнений о важной роли математики в музыке, при этом не стоит забывать о важной особенности музыкально-математических исследований: результаты применения численных методов все время должны проверяться человеческим ухом. 

3. Восприятие математики и музыки

Сегодня вряд ли кто-нибудь решится сводить музыку к определенным числовым действиям. Очевидно, надо начать с другого. Окружающий нас мир кроме звуков наполнен еще и ритмами. О чем говорит это слово? Посмотрите вокруг: ритмично звучат шаги, ритмичен ход часов, ритмично биение пульса человека, ритмично наше дыхание и т.д. И стоит нам услышать слово «ритм», как наши мысли невольно обращаются к музыке. И это понятно: ведь ритм – один из важнейших элементов музыки. На уроке сольфеджио обычно при изучении произведения «прохлопывают » ритм. Ритм в музыке — это сочетание размера и темпа. Если с темпом всё понятно, это «скорость» музыки, то размер представляет собой количество базовых длин звуков или пауз на один такт. Каким образом мы обычно считаем ритм музыки? Например, в вальсе чаще всего это повторение «раз-два-три, раз-два-три» — это есть ритм вальса, при этом каждая цифра означает долю, то есть составную часть одного такта. В приведённую фразу как раз помещается два такта, в каждом по три доли. В музыке под долей обычно имеется в виду одна четвертная нота, но возможны и другие варианты. В примере с классическим размером вальса это обычно три четверти, то есть в одном такте помещается ровно три равные длительности, которые, в свою очередь, могут быть разбиты на более мелкие по длительности звуки или объединены в более длинные.

В музыке мы имеем дело с короткими и длинными длительностями, они составляют основу любого ритма: целая нота, половинная, одна четверная, одна восьмая, одна шестнадцатая. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей. Мы видим, что длительности получаются так же, как дроби: они возникают при делении целой ноты на равные доли. Поэтому длительность можно подсчитывать как дробные числа, например:

+=

Равенство здесь надо понимать в том смысле, что длительность слева равна сумме длительностей справа. С помощью чисел то же равенство можно записать в виде 1/4 = 1/8 + 2/10

+ + = 1/1 = 1/4 + 1/4 + 1/2 и т.д.

Если все длительности в музыкальном произведении увеличить вдвое, произведение надо исполнять медленнее и наоборот.

4. Математическая чистота звука

Первым, кто в построении теории музыки отдавал приоритет слуховым ощущениям, был ученик Аристотеля Аристоксен. Основателем школы, ставившей во главу угла математические соотношения, был Пифагор. Его же признают создателем первой музыкальной теории.

Для своих исследований Пифагор использовал так называемый монохорд (в переводе с греческого — однострунный). Инструмент представлял собой четырехугольный ящик длиной около 1 метра, над верхней декой (доской) располагалась одна струна, ограниченная с двух сторон порожками. Под струной располагалась двигающаяся подставка, которая позволяла изменять высоту звука.

Вообще говоря, высота звука, издаваемого струной, определяется несколькими параметрами — длиной и толщиной струны, плотностью материала, из которого она изготовлена, натяжением и т.д. Когда свойства звука изучаются на монохорде, то толщина струны, ее натяжение и плотность материала остаются неизменными. Высота извлекаемого звука изменяется простым смещением подставки.

Частота, с которой колеблется вся струна целиком, определяет так называемый основной тон. Колебания частей струны вызывают появление обертонов. Самые сильный обертон возникает при колебаниях 1/2 части струны, слабее 1/3, 1/4, 1/5 и т.д. Соответственно соотношение частот (или высот) этих обертонов выглядит так: 1:2:3:4:5:6… Это так называемый натуральный или гармонический ряд звуков, и соответствующие обертоны тоже называются гармоническими.

5. Золотое сечение в музыкальных произведениях

«Золотое сечение» – это понятие, скорее, математическое и его изучение – задача науки. Это деление некой величины на две части в таком отношении, когда большая часть так будет относиться к меньшей, как целое к большей. Данное отношение оказывается равным трансцендентному числу Ф=1,6180339… с удивительными свойствами. Метод золотого сечения — это поиск значений функции на заданном отрезке.

Метод золотого сечения применяется и в музыке. Оказалось, что в музыкальных произведениях очень часто встречается эта золотая пропорция. В начале 20 века на заседании Московского музыкального кружка было сделано сообщение, содержащее информацию о том, какое применение находит золотое сечение в музыке.

С огромным интересом слушали члены музыкального кружка композиторы С. Рахманинов, С. Танеев, Р. Глиэр и другие. Доклад музыковеда Розенова Э.К. «Закон золотого сечения в музыке и поэзии» положил начало исследованиям математических закономерностей, связанных с золотой пропорцией, в музыке. Он проанализировал музыкальные произведения Моцарта, Баха, Бетховена, Вагнера, Шопена, Глинки и других композиторов и показал, что в их произведениях присутствует эта «божественная пропорция». Кульминация многих музыкальных произведений располагается не в центре, а немного смещена к концу произведения в соотношении 62:38 – это и есть точка золотой пропорции.

Доктор искусствоведения, профессор Л. Мазель заметил, изучая восьмитактные мелодии Шопена, Бетховена, Скрябина, что во многих творениях этих композиторов кульминация, как правило, приходится на слабую долю пятого, то есть на точку золотого сечения – 5/8.

Л. Мазель считал, что практически у каждого композитора – приверженца гармонического стиля можно найти подобную музыкальную структуру: пять тактов подъёма и три такта спуска. Это говорит о том, что метод золотого сечения активно применялся композиторами сознательно либо бессознательно.

Вероятно, такое структурное расположение кульминационных моментов придает музыкальному произведению гармоническое звучание и эмоциональную окраску. Серьёзное исследование музыкальных произведений предпринял композитор и музыковед Л. Сабанеев. Он изучил около двух тысяч творений разных композиторов и пришёл к выводу, что примерно в 75% случаев золотое сечение присутствовало в музыкальном произведении хотя бы один раз. Самое большое количество произведений, в которых встречается золотая пропорция, он отмечал у таких композиторов, как Аренский (95%), Бетховен (97%), Гайдн (97%), Моцарт (91%), Скрябин (90%), Шопен (92%), Шуберт (91%).

Итак, можно наблюдать огромное количество примеров применения математических понятий в музыке. Не зря говорят, что музыка глубоко математична.

11

6. Практическая часть

Меня заинтересовал вопрос: если математика и музыка теоретически связаны, то как это доказать на практическом примере? В этот момент к нам в голову пришла идея: а что, если попробовать выявить творческие способности человека с помощью нотной грамоты и даты рождения? Суть моего исследования заключалась в следующем:

• У конкретного человека бралась полная дата рождения. ( к примеру, 24.02.2001)

• Потом нумеровались ноты на нотном стане: до-0; ре-1; ми-2; фа-3; соль-4; ля-5;

си-6; до-7.

• Дата человека переводилась на нотный стан. Таким образом, «музыка» нашего человека будет: ми; соль; до; ми; ми; до; до; ре.

• Нажимаем на клавишах пианино все эти ноты сразу.

• Делаем вывод: если получившийся аккорд звучит приятно и благозвучно, значит человек творческий; если же аккорд не благозвучен, то человек точен.

Я решила протестировать несколько человек:

(см. Приложение 1)

1) Яндакова Светлана,24.03.2000. Рисование, фотограф. – Благозвучно.

2) Кузьмина Виктория, 12.04.2000. Модель. — Не благозвучно.

3) Никитин Василий, 27.12.1999. Плавание, футбол, бокс. – Благозвучно.

4) Хурамаев Николай, 13.11.2000. Плавание, футбол, кулинария. — Не благозвучно.

5) Родионова Анжела, 08.10.2000. Пение, поэзия. – Благозвучно.

6) Матвеева Елена, 02.05.2000. Танцы. – Благозвучно.

7) Федотов Андрей, 06.05.1997. Компьютерные технологии. — Не благозвучно.

8) Мышкова Виктория, 05.01.2001. Танцы. – Благозвучно.

9) Макарова Татьяна, 26.01.1994. Проектные работы. – Не благозвучно.

10) Николаева Людмила Николаевна, 19.10.1971. Преподаватель математики. – Не благозвучно.

11) Аверьянов Дмитрий, 15.04.1990. Спортсмен. – Не благозвучно.

12) Антонова Александра, 13.08.2000. Рисование, пение, танцы. – Благозвучно.

13) Луканов Максим, 30.03.1997. Бокс. – Не благозвучно.

14) Куракина Марина, 19.06.1992. Модель. – Не благозвучно.

15) Васин Дмитрий, 15.11.1999. Карате. – Благозвучно.

16) Арефьева Анастасия, 15.01.2000. Иностранный язык. – Благозвучно.

17) Степанов Егор, 05.02.2004. Бокс. – Не благозвучно.

18) Антонова Дарья, 17.04.2005. Рисование. – Благозвучно.

7. Музыкальные задачи

1) Сколько четвертых в одном такте? (счет такта )

2) Чайковский был выдающийся композитором. Он родился в 1840 году. А умер в 1893 году. Сколько лет он жил? Прожил ли он больше пол века?

3) Найдите среднее арифметическое музыкальных инструментов. Если пианино весит 22 кг, а гитара 2 кг.

4) У трех друзей по 3 гитары из трех видов дерева: дуб , сосна и осина. Известно, что у первого друга 2 гитары из дуба, у другого 3 гитары из осины. Сколько гитар из сосны? Из какого материала гитар больше всего?

5) Какая нота стоит между до и ля?

6) Сколько разных способов существует, чтобы расставить 3 человека в трио?

7) Счет такта 2/4. Одна нота составляет 1/8, другая-1/4.Чему равна третья нота?

ОТВЕТ: 1) 1/4 + 1/8=3/8 2) 2/4 — 3/8 = 1/8.

9) Счет такта C (что в переводе на язык музыкантов- 4/4). В него входят две восьмые и четверть. Какова длительность оставшиеся ноты? ОТВЕТ:1/8 + 1/8 + 1/4= 2/4 — 1/2= 1/2, т.е половина.

13) Масса одной гитары — 11,2 кг. Это 1/100 от массы фортепьяно. Чему равна его масса? Найдите и округлите до десятков. ОТВЕТ: 11,2 : 1/100=1120(кг) ~112(кг)

14) «ПОЛЕЗНОЕ С ПРИЯТНЫМ»

а) Возьмите ноту си. Прибавьте ноту. Вычтите две ноты.

Ответ: фа.

б) Была нота четверть. Поставили точку. Какая теперь нота получилась?

ОТВЕТ: половина.

с) Какие две ноты в фамилии Сидоров? ОТВЕТ: СИДОров. (си, до)

15) В такте две восьмые, одна четверть. Чему равен такт? Ответ:1/8+1/8+1/4=2/4

16) В музыке есть такие ноты, как шестнадцатые. Они равны половине восьмой.

Что такое две шестнадцатые? Ответ:1/16+1/16=2/16=1/8

8. Заключение

Изучив большое количество литературных и интернет-источников , я окунулась в мир информации и узнала о множестве фактов в области использования математических понятий в музыкальном мире. Интересна история вопроса. Оказывается, многие ученые прошлого делали попытку представить музыку как математическую модель. Одним из первых выразил красоту музыки с помощью чисел, а именно отношений, древнегреческий ученый Пифагор.

Проведенное исследование позволило нам сделать следующие выводы: для определения частоты нот используют обыкновенные дроби и действия над ними. Дробные числа также используются для обозначения тактов. Для обозначения нотных символов широко используются графики и системы координат (чисто математические понятия). Тона и полутона симметричны. Также симметрично расположение клавиш на клавиатуре.

В результате проведенного исследования мы выяснили, что многие композиторы издавна использовали математические законы для написания своих произведений, например, «Золотое сечение». Этот метод золотой пропорции активно применялся композиторами сознательно либо бессознательно. Такое структурное расположение кульминационных моментов придает музыкальному произведению гармоническое звучание и эмоциональную окраску.

Главный вывод, который я сделал: связь музыки с математикой — одна из древнейших. В самом широком смысле можно сказать, что весь мир — это музыка, потому что музыка — это математика. На подчиненность музыкальных структур математическим законам люди обратили внимание не одно тысячелетие назад. Их исследования показали, что многие вопросы, связанные с природой музыки и ее воздействием на человека могут быть описаны языком математики.

15

9. Список использованной литературы

1. Бореев Г. Пифагор. Жизнь-как учение./ Георгий Бореев.- М. Гиперборея, 2008.

2. Булучевский Ю. Краткий музыкальный словарь./ Фомин В.- М.: Музыка, 2005.

3. Волошинов А. В. Математика и искусство/ М.: Просвещение, 1992 — с.335

4. Гейн А. Г., Касымов А. О. «Математика и музыка».

6. Ценова В. С. Числовые тайны музыки: Монографическое исследование./ М.: Московская гос. консерватория имени П. И. Чайковского, 2000.

7. Математика и музыка [Электронный ресурс]./ О детстве. — URL: http://www.o-detstve.ru/forchildren/research-project/4579.html (дата обращение: 17.02.2017)

8. Основные сведения о музыке [Электронный ресурс].- URL: http://www.0zd.ru/matematika/svyaz_matematiki_s_muzykoj.html (дата обращения: 17. 02.2017)

16

10. Приложение 1

17

infourok.ru

Исследовательская работа «Музыка и математика»

Министерство общего и профессионального образования

Ростовской области

муниципальное общеобразовательное учреждение

средняя общеобразовательная школы № 8

Музыка и математика

Выполнила: Лебедь Диана,

ученица 5 а класса.

Руководитель: Голубова

Наталья Валерьевна,

учитель математики.

Волгодонск, 2015

Содержание

1. Введение 3

2. Связь между музыкой и математикой 3

3. Практическая часть

3.1Создание математической модели музыкального фрагмента 5

3.2Транспонирование мелодии с помощью математической модели. 7

3.3Исследование дат рождения 8

4. Заключение 11

5. Список литературы 12

ВВЕДЕНИЕ

«Музыка есть таинственная арифметика души;

Она вычисляет, сама того не подозревая»

Г.Лейбниц.

Актуальность: На одном из занятий кружка, когда я сказала, что у меня не очень хорошие способности по математике, моя учительница спросила о моих успехах по сольфеджио. Услышав мой ответ, что по сольфеджио у меня хорошие успехи, Наталья Валерьевна сказала, что и по математике должно быть хорошо. Я задумалась над тем, что услышала. Действительно, мне нравятся уроки математики, люблю решать задачи. Нравится музыка и игра на фортепиано, пение. Неужели такие две совершенно разные области как математика и музыка взаимосвязаны? В своей работе я выдвинула следующую гипотезу: любое музыкальное произведение можно представить, как некую математическую модель.

Цель: на примере музыкальных произведений выявить взаимосвязь между музыкой и математикой.

Задачи:

1.Выяснить, были ли в истории попытки связать музыку с математикой.

2. Провести свое исследование по установлению связи между музыкой и цифрами, рассмотрев музыкальные произведения как математическую модель.

3. Переложить числа (даты рождения одноклассников) на музыку. Установить связь между звуками и способностями личности.

Объект исследования: музыка и математика.

Методы исследования:

1.Изучение, обработка и анализ документов.

2.Метод исследования музыкального произведения.

3.Метод проблемно-поисковой ситуации.

СВЯЗЬ МЕЖДУ МУЗЫКОЙ И МАТЕМАТИКОЙ

Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.

В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.

Свое отношение к математике и музыки ученые высказывались в своих личных переписках. Так, к примеру, Лейбниц в письме Гольдбаху пишет: “Музыка есть скрытое арифметическое упражнение души, не умеющей считать”. На что Гольдбах ему отвечает: “Музыка – это проявление скрытой математики”.

История знает массу людей, талант которых многогранен и способности к одному роду занятий как бы дополняют способности к другому. Леонардо да Винчи был скульптором, художником, архитектором, инженером; пел, преподавал пение и был первым, кто изучил природу вокального искусства.

Александр Сергеевич Грибоедов, русский писатель и дипломат, был еще композитором, пианистом и органистом. Михаил Иванович Глинка прекрасно рисовал. Эйнштейн играл на скрипке… Дети, обучающиеся музыке, обычно обнаруживают способности и тягу к другим видам искусства, потому что, помимо когнитивных способностей, музыка развивает эмоции, улучшает личностные качества. 

Однако, одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.

Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Родился Пифагор около 570 года до нашей эры на острове Самосее. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева. Они проводили занятия математикой под музыку, так как заметили, что она благотворно влияет на интеллект. Он учился музыки в Египте и сделал ее предметом науки в Италии. Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать. Исследованию музыки посвящали свои работы многие величайшие математики, такие как: Рене Декарт ( его первый труд — “Compendium Musicae” в переводе “Трактат о музыке” ) , Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие.

Вывод. «Раздумывая об искусстве и науке, об их взаимосвязях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая и духовная деятельность человека. Что между ними размещается все, что человечество создало в области наук и искусства» – писал Г. Нейгауз. Изучив работы ученых, мною было установлено, что в прошлом были неоднократные попытки рассматривать музыку, как один из объектов изучения математики. Таким образом, многие учёные в древности считали, что гармония чисел является сродни гармонии звуков и дополняет друг друга, музыку и математику.

ПРАКТИЧЕСКАЯ ЧАСТЬ.

Создание математической модели музыкального фрагмента.

Рассмотрим фрагмент польки А. Спадавеккиа «Добрый хук» из кинофильма «Золушка». Попробуем сделать математическую модель этого произведения: каждой ноте соответствует номер ступени. Цифра 1 – I ступень, 2 – II ,3 – III, 4 – IV, 5 – V ,6 – VI ,7 – VII, 8 – I, 9 – II ,10 – III. Переложили ноты на числа и получили при этом такой ряд чисел:

Правая рука: 3553 l 455 l 466 l 531 l 3553 l 455 l 3653 l 1 II

Левая рука 1535 l 2545 l 2545 l 1535 l 1535 l 2545 l 2545 l 351 II

Черта между цифрами служит тактовой четой, то есть делит их на такты, так как сделано в произведении.

В музыке есть понятие – устойчивые ступени, на которых строится тоническое трезвучие (Т5/3): 1, 3, 5 ступени.

Если в каждом полном такте сложить номера устойчивых ступеней, то мы заметим следующую закономерность:

Правая рука

Левая рука

1 такт

3+5+3+5=16

1+5+3+5=14

2 такт

4+5+5=14

2+5+4+5=16

3 такт

4+6+6=16

2+5+4+5=16

4 такт

5+3+1=9

1+5+3+5=14

5 такт

3+5+3+5=16

1+5+3+5=14

6 такт

4+5+5=14

2+5+4+5=16

7 такт

3+6+5+3=17

2+5+4+5=16

8 такт

1

3+5+1=9

Наблюдаем, что в произведении есть повторяющиеся группы чисел и для левой руки: 16,14,16,9,16,14,17,1 и для правой руки 14,16,16,14,14,16,16,9 – это 14,16.

Ритм – один из важнейших элементов музыки. Ритм – чередование длительностей. Рассмотрим ритм 3/4, музыканты называют его размером. В такте могут встречаться такие чередования длительностей:

1.

3.

2.

7.

6.

5.

4.

В музыке существуют и другие размеры ,

Рассмотрим ритм, размер чередования длительностей: 1/2 I 1/4 1/4 I 1/8 1/8 1/ 8 1/8 II

Правая рука

Левая рука

1 такт

1/8+1/8+1/8+1/8=4/8

1/8+1/8+1/8+1/8=4/8

2 такт

1/8+1/8+1/4=2/8+1/4=4/8

1/8+1/8+1/8+1/8=4/8

3 такт

1/8+1/8+1/4=2/8+1/4=4/8

1/8+1/8+1/8+1/8=4/8

4 такт

1/8+1/8+1/4=2/8+1/4=4/8

1/8+1/8+1/8+1/8=4/8

5 такт

1/8+1/8+1/8+1/8=4/8

1/8+1/8+1/8+1/8=4/8

6 такт

1/8+1/8+1/4=2/8+1/4=4/8

1/8+1/8+1/8+1/8=4/8

7 такт

1/8+1/8+1/8+1/8=4/8

1/8+1/8+1/8+1/8=4/8

8 такт

1/2

1/8+1/8+1/4=2/8+1/4=4/8

Сумма длительностей в каждом такте равна размеру 2/4=1/2=4/8.

Найдем сумму длительностей всех нот музыкальной фразы: 4/8+4/8+4/8+4/8+4/8+4/8+4/8+1/2=28/8+1/2=7/2+1/2=8/2=4

Сумма всех длительностей в музыкальной фразе равна целому числу.

Значит, зная ступени, длительности нот, размер я могу записать эту пьесу в любой другой тональности или от другой ноты, т. е. транспонировать.

Транспонировние. «Плясовая».

Проставив ступени и записав длительности нот, я получила математическую модель пьесы, чтобы не перепутать октавы я поставила стрелочки, но можно было у каждой ступени указать номер октавы.

1.Последовательность ступеней 1512 321 21# 7 1 2 5 11 1624 321 5#6#7122 11

2.Размер 2/4 и длительности: 1/8 1/8 1/8 1/8 1/8 1/8 1/4 1/16 1/16 1/16 1/16 1/8 1/8 1/4 1/4 1/8 1/8 1/8 1/8 1/8 1/8 1/4 I /16 1/16 1/16 1/16 1/8 1/8 1/4 1/4

3. Сложила устойчивые ступени, получила последовательность 8,4,7,2,1,4,6,2. Повторение чисел есть , 4 повторяется через 3 цифры и 2 повторяется через 3 цифры.

Правая рука

1 такт

1+5+2=8

2 такт

3+1=4

3 такт

1+1+5=7

4 такт

1+1=2

5 такт

1

6 такт

3+1=4

7 такт

5+1=6

8 такт

1+1=2

Затем записала гамму от ноты фа и проставила номера ступеней:

Проставила ступени в каждом такте и записала мелодию.

В своей исследовательской работе я выдвинула гипотезу о том, что любое музыкальное произведение можно представить как математическую модель.

По изложенному в работе способу перевода из нот в числовой ряд следует, что моя гипотеза верна, так как способов перевода может быть несколько. В работе я рассмотрела два способа: запись мелодии по ступеням и сложение устойчивых ступеней, запись ритмического рисунка с помощью дробей. Данная модель помогла транспонировать мелодию в другую тональность.

Исследование дат рождения

Следуя теории Пифагора, числа обладают абсолютной властью над всеми событиями, над всеми живыми существами, а значит, числа правят музыкой. В своих работах он утверждал, что музыка подчиняется высшему закону (математике) и вследствие этого восстанавливает в организме человека гармонию.

Нумерология – паранаука о числах. Нумерология имеет еще одно распространенная название – магия чисел. В нумерологии все слова, имена, числа можно свести к единичным разрядам (однозначным человеком), которые соответствует оккультным характеристикам, влияющим на жизнь человека. Это значит, что каждому числу, согласно нумерологии, соответствует определенные свойства, образы и понятия. Нумерологию используют для определенного характера человека, его природных способностей для выявления сильных и слабых сторон его личности, а также для определения характера человека, его природных способностей, для выявления сильных и слабых сторон его личностей, а также для определения подходящих профессии, места проживания и многих других факторов.

Даты рождений – это ряд чисел. Попробуем установить связь между числами и музыкой.

Мною были исследованы даты рождений 12 учащихся 5а класса, в котором я обучаюсь. Как известно дата – набор цифр. Мы предложим даты на ноты. В таблице, где знак «– », мелодия звучала негармонично, а значит, диссонанс. А если мелодично, то знак « + » – это консонанс. Каждой ноте мы присвоили номер ступени. До – 0, ре -1, ми – 2, фа – 3, соль – 4, ля – 5, си – 6, до– 7, ре – 8, ми – 9.

У каждого человека получилось по мелодическому ряду:

№

ФИ

Дата

Нотная последовательность

увлечения

1

Борцов Евгений

18.06.2003

_

акробатика

2

Горяинова Надежда

26.09.2003

_

литература, биология

4

Калачева Дарья

04.01.2003

_

особых увлечений нет, успехи в точных науках

5

Кирман Алина

05.09.2003

_

спорт, точные науки, танцы

10

Макарова Марина

26.12.2002

_

точные науки, танцы

6

Козлова Татьяна

08.03.2003

+

спорт, танцы

7

Лебедь Диана

11.10.2003

+

музыка

8

Малашенко Виктор

08.09.2003

+

конструирование, хорошо поет

9

Плотников Петр

07.08.2003

+

Хорошо поет, конструирование, точные науки

3

Жукова Арина

21.09.2003

+

художественная школа

После того, как мы переложили даты рождения на мелодию, попробуем установить связь между звучанием даты рождения и способностями человека.

I Группа (дети, у которых мелодии благозвучные):

№

ФИ

Дата

Нотная последовательность

увлечения

6

Козлова Татьяна

08.03.2003

+

спорт, танцы

7

Лебедь Диана

11.10.2003

+

музыка

8

Малашенко Виктор

08.09.2003

+

конструирование, хорошо поет

9

Плотников Петр

07.08.2003

+

Хорошо поет, конструирование, точные науки

3

Жукова Арина

21.09.2003

+

художественная школа

II группа (дети, у которых мелодии звучали «резко»):

№

ФИ

Дата

Нотная последовательность

увлечения

1

Борцов Евгений

18.06.2003

_

акробатика

2

Горяинова Надежда

26.09.2003

_

литература, биология

4

Калачева Дарья

04.01.2003

_

особых увлечений нет, успехи в точных науках

5

Кирман Алина

05.09.2003

_

спорт, точные науки, танцы

10

Макарова Марина

26.12.2002

_

точные науки, танцы

Методом опроса я выяснила, чем каждый ученик увлекается.

Дети класса творческие люди на это влияют их даты рождения. В первой группе, музыкальный ряд звучал мелодичнее, большинство детей с творческими наклонностями: некоторые из них занимаются в художественной школе или танцами. Данная группа детей обладает творческими способностями, косвенно или напрямую связана с музыкой.

Во второй группе, где музыкальный звучал «резко», надо отметить, что очень «резко, даже безобразно» звучащих не было, большинство детей занимаются изучением точных наук, техническим моделированием, предпочитают занятия спортом.

Следует отметить, что в исследуемой группе оказались те, кто по тем или иным причинам ничем не увлекаются и не занимаются в каких либо секциях. Предполагаю, что возможно, они имеют эти склонности, но они ещё не реализовали их.

Вывод: большее количества учащихся класса имеют творческие способности. Возможно, именно с этим связанно активное участие класса во всех школьных мероприятиях, свободно организуем классные вечера, концерты для родителей.

Мои исследования оказались интересны не только мне, но и одноклассникам.

ЗАКЛЮЧЕНИЕ.

В результате проделанной работы мною были выполнены поставленные задачи. Рассмотрела связь ритмов и чисел, дробей и длительностей нот. Работа над этой темой позволила выявить много интересной информации о закономерностях, которые встречаются в музыке и математике. Построила математическую модель музыкального произведения полька «Добрый жук» из к/ф « Золушка». Установила связь между датами и ступенями, переложила даты рождений одноклассников на музыку. Но для утверждения того, что звучание даты рождения определяет определенный тип особенностей человека, необходимо большее количество исследуемых.

Возможность перевода нот в числовой ряд подтверждает мою гипотезу. Математика – царица наук, тесным образом перекликается с музыкой. Несомненно, математика пронизывает музыку.

Выполняя работу, я отметила, что в мелодии постоянно происходит чередование сильных и слабых долей, чередование тактов, где сильных долей больше с тактами, где меньше или только одна сильная доля, что музыкальная фраза заканчивается 1 ступенью. Если проанализировать больше произведений и более сложные музыкальные формы, то вероятно можно выявить еще закономерности. Также мне пришла идея попробовать одну и ту же последовательность нот записать в разных ритмических рисунках, а может и придумать свою композицию, например, по «красивой» числовой последовательности.

Список литературы:

1. Деплан И. Я. Мир чисел. М.: «Просвещение», 2005

2.Дэвид Филипс. Нумерология и открытие внутреннего “Я”. Полное практическое руководство. СПб: София, 2007, 256с.

3. Жмудь Л. Я. Пифагор и его школа М.: Наука, 1990, 192с.

4. Холопов Ю. Н. Консонанс и диссонанс // Музыкальный энциклопедический словарь. М.: Советская энциклопедия, 1990.

5. Сольфеджио 2 класс

6. Энциклопедия для детей. Т. 7. Искусство. Ч. 1. – Э68-е изд., испр./Глав. Ред. М.Д. Аксенова. – М..6 Аванта +, 2006 – 688 с.: ил.

7. Энциклопедический словарь юного математика. М.; «Педагогика» 1985г

12. Я познаю мир: Детская энциклопедия: Музыка /авт. А.С. Кленов. Под общей ред. О.Г. Хинн. – М.: ООО Фирма «Издательство АСТ», 2010. – 46

Интернет ресурсы:

1.http://www.stonot.ru/

2.http://www.krugosvet.ru/

3.http://www.wikipedia.org/

4. http://ru.wikibooks.org/wiki

5.http://www.piano-notes.net/

infourok.ru

Математика в музыке

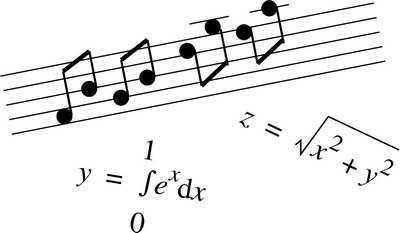
«Математика является наукой, которая рассматривает отвлеченное количество… Она подразделяется на следующие части: арифметика, музыка, геометрия и астрономия. Арифметика — учение о количестве, выражаемом числом. Музыка же — учение, которое рассматривает числа по отношению к тем явлениям, которые наблюдаются в звуке…» Так писал римский ученый Кассиодор. Дело было в шестом веке, в доброе старое время, когда биология еще не отделилась от физики, а химии не существовало вовсе. Сегодня мало кому придет в голову объявить музыку составной частью математики. В течение столетий возникло классическое противопоставление науки и искусства. Но наша эпоха, которая, помимо многих других эпитетов, с основанием может называться веком синтеза различных наук, по мнению автора, становится также веком синтеза науки и искусства. В настоящее время пример подобных тенденций являют, по-видимому, математика и музыка.

Математический синтез и математический анализ музыки

Этот контакт проявляется при постановке и решении двух основных проблем: математического анализа и математического синтеза музыки. В чем заключаются эти проблемы? Каково их отношение к традиционному, нематематическому музыкознанию?

Музыковедение всегда видело одну из своих основных задач в исследовании, в анализе музыки — с точки зрения мелодики, гармонии, ритмики, формы, инструментовки. Наша первая проблема состоит в использовании для этой цели различных математических дисциплин — статистики, теории информации, теории групп. Оговоримся сразу же: математический анализ музыки и традиционный анализ музыкальных произведений не исключают друг друга. Наоборот, для математического анализа музыки всегда в каком-то объеме необходим предварительный «нематематический» анализ. Результаты же математического анализа не противоречат результатам традиционного анализа, а уточняют их.

Другая основная задача теории музыки с давних пор заключается в ее педагогической функции. Будущий композитор обучается теории музыки, начиная с нотной грамоты, за которой следует учение о гармонии, о музыкальных формах и т д. Проблема математического синтеза музыки вполне аналогична этой задаче, с той «лишь» разницей, что обучать сочинению следует не человека, а машину. Как читатель догадывается, слово «лишь» в предыдущую фразу вставлено в ироническом смысле. В том-то и дело, что человек не машина (точнее, наоборот: современные машины не человек)!

Ведь будущий композитор — обладатель человеческой психики, самого сложного продукта материи. Благодаря этому разные советы и правила он схватывает «на лету», даже если они сформулированы не совсем точно. Пользуясь своим личным вкусом, ученик может оценить, хорошо или плохо звучит музыка, несмотря на то, что он, как правило, не в состоянии объяснить, какими признаками или формальными критериями он при этом руководствовался. Наконец, в его распоряжении фантазия — неиссякаемый источник новых музыкальных идей. Воистину не мудрено из такого великолепного материала сделать композитора! Но попробуйте сделать композитора из вычислительной машины, которая, правда, всему может научиться, но сама не знает ничего.

Даже наиболее элементарные вещи машине требуется сообщать точно и подробно, ничего для нее не подразумевается само собой. Никакого вкуса у нее нет, ибо нет музыкального опыта. И уж совершенно безнадежно выглядит дело с машинной фантазией. Откуда ей взяться?

После всего сказанного у читателя законно возникает вопрос: зачем тогда вообще стараться при помощи машин отнимать хлеб у композиторов-людей? Похоже, что дело это невозможное, да, собственно, и ненужное. Ответим со всей определенностью: никто при помощи «машинной музыки» не собирается превратить композиторов в безработных. Цель серьезных экспериментов по машинному сочинению состоит в другом, и эта цель упомянутыми выше трудностями не снимается, а становится еще более привлекательной. К последнему утверждению мы еще вернемся несколько позже. Теперь, не углубляясь в проблематику анализа, рассмотрим несколько более подробно вопросы, связанные с математическим синтезом музыки.

Но, прежде всего, следует отметить одно обстоятельство, о котором неспециалисты часто забывают. В нашей проблеме речь не идет о конструировании какой-то новой машины неизвестного до сих пор типа, которая будет способна к сочинению музыки. Такие машины уже построены и существуют во многих тысячах экземпляров. Ибо для этой цели пригодна любая универсальная электронная вычислительная машина. Весь вопрос состоит в том, как научиться составить такую последовательность инструкций, такую программу, следуя которой машина сочинит музыку. Итак, выражения «машина может» или «машина не умеет», по существу, следует читать «программа может» или «программа не умеет». Но программу составляет не машина, а человек, поэтому от него, в конечном счете и зависит успех или неуспех машины. Однако читатель ни в коем случае не должен думать, что программист заложил в машину разные мелодии и потом заставил машину эти же мелодии «сочинить». На самом деле автор программы сам не знает, что сочинит машина. Как же в таком случае происходит процесс синтеза? Как преодолеваются упомянутые выше трудности на этом пути?

Законы строгие и нестрогие

Сначала вернемся к вопросу о строгих, категорических правилах, которые должен соблюдать каждый композитор. Сообщение таких правил машине — дело хлопотное и трудоемкое, однако никаких принципиальных затруднений здесь нет. При проверке оказывается, что таких правил в музыке гораздо меньше, чем обычно принято думать. Поэтому включение этих правил в программу еще далеко не решает вопроса.

Относительным исключением в этом смысле являются, пожалуй, только весьма специфические ситуации. В качестве одного примера можно привести так называемый «строгий стиль», который характеризовал многоголосную (главным образом вокальную) музыку в эпоху Возрождения. Это самая старая музыка, которая изредка может быть услышана в концертах. Другой пример принадлежит уже нашему времени — это додекафойная музыка в своей последовательной реализации. В упомянутых двух стилях свод строгих законов в сравнительно большой степени характеризует музыку. Вследствие этого процесс сочинения легче поддается программированию. Именно поэтому, вероятно, сюита «Иллиак» для струнного квартета, сочиненная вычислительной машиной Иллинойсского университета, начинается в строгом стиле, а кончается додекафонией.

Никакой «середины» нет. Но в огромном своем большинстве та музыка, которую мы слышим в концертах, по радио относится именно к этой «середине», к так называемой тональной музыке. Тональную музыку писали Бах, Гайдн, Моцарт, Бетховен, Шуберт, Глинка, Чайковский, Рахманинов, Скрябин, Прокофьев. Тональную музыку пишет большинство современных композиторов. Но сочинение тональной музыки труднее поддается программированию.

В чем заключается основная трудность алгоритмизации сочинения тональной музыки? Дело в том, что законы тональной музыки в своем большинстве не являются категорическими приказами, а лишь рекомендациями. Например, как в мелодии, так и в гармонии наблюдается стремление к первой, основной ступени лада. Это проявляется хотя бы в том, что в большинстве случаев мелодия в конце произведения достигает первой ступени. Но это закон с очень многими исключениями, так что нельзя даже говорить о законе в строгом смысле слова. Можно лишь отметить некоторую господствующую тенденцию.

Именно в подобных тенденциях — вся суть тональной музыки. Благодаря приобретенному ранее музыкальному опыту композитор эти тенденции ощущает интуитивно и в одной конкретной ситуации отдает предпочтение одному направлению развития музыкальной мысли, отвергая некоторые иные рекомендации, а в другой ситуации поступает наоборот. Можно ли помочь машине приобрести нечто подобное такой интуиции?

Отложим, однако, на время решение этого вопроса и обратимся к проблеме фантазии очень важного компонента любого творчества. Как увидим, оба вопроса удается решить одним и тем же методом.

Направленная случайность

Общефилософские категории необходимого и случайного проявляются в каждом виде искусства. Не может быть произведения искусства, которое не подчинилось бы каким-то закономерностям, каким-то правилам, выделяющим «дозволенные приемы». Но ни одно произведение искусства не оказывается жизнеспособным, если фантазия художника не привела к оригинальному, одновременно неожиданному и естественному сочетанию элементов. Законы, которым подчиняется фантазия, могут быть (и бывают) неизвестны самому художнику, он тоже не может предугадать, что ему фантазия подскажет в следующий миг. Поэтому есть основание считать работу фантазии не строго детерминированным, а случайным процессом. Все сказанное относится, в частности, и к музыке.

Откуда же наша бедная вычислительная машина возьмет фантазию? Ведь конструкторы машины считали своим долгом добиться того, чтобы машина не капризничала, чтобы она непреклонно и точно следовала программе и однозначно выполнила бы ее. Работа машины нам кажется самим олицетворением точности и детерминированности.

Это действительно так, если иметь в виду нежелательные ошибки в работе машины. Но в то же время даже при выполнении поручения математиков машину иногда нарочно заставляют действовать случайно, непредсказуемо. Конечно, именно в тех ситуациях, когда этого хочет программист. При помощи подобною подхода реализуется в современной математике так называемый метод Монте Карло, который оправдывает себя во многих вычислительных задачах. В связи с этим придуманы специальные приемы, позволяющие машине выбрать случайное число — например, случайную дробь (число между нулем и единицей). (К слову подобным образом работают игровые автоматы на https://vulkanstavka-777-club.com).

Таким образом, в работу машины может быть введена случайность, имитирующая фантазию художника. Однако эта фантазия не должна быть слепой. При сочинении мелодии композитор не берет ноты наугад, а выбирает одни звуки чаще, другие — реже; после большого скачка в мелодии, как правило, выбирается плавный ход и т. п. Такой направленный способ действия доступен и машине. Поясним это на очень простом примере.

Допустим, что машина должна строить ритмический рисунок, выбирая длины ног. Предположим, что характер музыки таков, что восьмые должны преобладать над четвертями, скажем, появляться в среднем в три раза чаще. Этого легко добиться при помощи случайных чисел, если поступать следующим образом. Условимся, что дробь от 0 до 0,75 будет означать, что машина выбрала («сочинила») одну восьмую, а дробь от 0,75 до 1,00 будет означать выбор одной четвертой. Пусть теперь случайная дробь оказалась равной 0,31. Это событие можно рассматривать как элементарный «акт вдохновения», в результате которого пишется нота длины одна восьмая. Число же 0,76 означало бы выбор одной четверти, и т. д. В среднем такая тактика, как легко понять, даст нам восьмых в три раза больше, чем четвертей, но в то же время для каждой отдельной ноты предсказать ее длину невозможно она зависит от «машинного вдохновения», то есть от непредсказуемого заранее значения случайной дроби.

Подобный метод можно использовать как для выбора ритмического рисунка, так и для выбора высоты нот (или же для последовательности интервалов, из которых построена мелодия), для подбора сопровождения, для решения вопроса о форме сочинения и т. д. При этом от распределения вероятностей, которые мы предпишем машине, будет зависеть общий характер синтезируемой музыки, но в то же время мы никак не сможем предугадать, какой точный вид будет иметь следующий «опус» машины. Элемент неожиданности здесь проявляется примерно в такой же степени, как у композитора-человека.

Оставшийся выше нерешенным вопрос о том, как при математическом синтезе музыки моделировать предыдущий опыт композитора, его вкус, то есть предпочтение одних средств выражения по сравнению с другими, можно решать именно при помощи соответствующего подбора вероятностей. Таким же образом можно включать в процесс синтеза правила типа рекомендаций: машина бросит жребий и в зависимости от результата решит, следовать в конкретном случае данной рекомендации или нет.

Таким образом, композитор-автомат получает принципиальную возможность обзавестись фантазией — она дается использованием случайности, только не слепой случайности, а направленной при помощи подходящего выбора вероятностей.

Тем самым снимается возражение, которое высказывалось по адресу машинного синтеза музыки, а именно, что результатом синтеза может быть только либо застывшее, неинтересное произведение, которое получено «по всем законам», но лишено оригинальности, либо нечто невообразимо хаотическое, полученное при следовании слепой случайности.

Новые проблемы

Однако принципиальная возможность программы синтеза не означает, что такая программа, отвечающая всем требованиям, уже в наших руках сегодня или будет готова завтра. Для практического составления программы требуется, во-первых, знание тех правил, которые должны выполняться безусловно, во-вторых, нужно указать те параметры, значения которых будут выбираться случайно, и, в-третьих, следует дать распределение вероятностей для этих параметров. Кроме того, нужен сам алгоритм синтеза, то есть следует указать, в какой последовательности будут выбираться значения всех нужных параметров. Этот вопрос является существенным потому, что вероятности выбора одного параметра могут зависеть от уже выбранного значения какого-то другого параметра.

Решение указанных вопросов ставит перед теорией музыки новые, непривычные вопросы. Традиционное музыкознание, как правило, ответа на эти вопросы не дает. Уже в самом факте постановки новых задач хочется видеть заслугу проблемы машинного синтеза музыки. Для их решения приходится использовать как результаты традиционного музыкознания, так и методы математического анализа музыки. Иллюстрируем это одним примером.

В тональной музыке весьма распространенным приемом для построения мелодии является метод секвенцирования. Под этим понимается повторение некоторого мотива с известным сдвигом вверх или вниз. Музыковед Л. Мазель в своей работе «О мелодии» высказывает интересные мысли о том, какие секвенции характерны для музыки того или другого стиля. Рассматривались прелюдии и фуги Баха, симфонии Гайдна и произведения Чайковского. Полученные результаты позволяют уточнять тезисы традиционного музыкознания. Кроме того, они могут использоваться при синтезе музыки. Таким образом, математический анализ музыки дает сведения, необходимые для синтеза.

Но и наоборот — результаты синтеза позволяют судить о том, насколько глубоко и успешно был проведен анализ. Тем самым впервые за многовековую историю науки о музыке результаты работы музыковеда смогут проходить экспериментальную проверку. Устраняя замеченные дефекты, мы получим уже лучшую программу синтеза и т. д.

При составлении алгоритма синтеза, как уже говорилось, мы опираемся также на достижения традиционной науки о музыке, в том числе на результаты психологии музыкального творчества. Думается, что проблематика синтеза музыки дает ощутимый импульс для дальнейшего развития этой науки. Ведь машина моделирует — сначала по крайней мере в смысле результата — работу композитора. Значит, успех или неуспех модели позволяет судить о ценности тех приемов, которые были положены в основу построения модели. Если эти приемы оказались успешными, то можно надеяться, что они имеют некоторое отношение к тем процессам, которые совершаются в психике композитора. Тем самым результативное моделирование постепенно перерастает в функциональное моделирование.

То, что сегодня мы еще многого не знаем о работе психики, не должно стать причиной отказа от экспериментов по синтезу музыки. Наоборот, постепенно достигаемые успехи в задаче синтеза могут способствовать исследованию психики, точнее — развитию психологии творчества.

Автор: В. Детловс.

www.poznavayka.org