Магические квадраты 2 класс математика: МАгические квадраты (2 класс)
МАгические квадраты (2 класс)

Курс профессиональной переподготовки
Учитель начальных классов

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: 171886
Похожие материалы
Оставьте свой комментарий
Тема: Логические задачи с числами и цифрами. Магические квадраты.
Цель: углубить знания учащихся в области математики, показать взаимосвязь различных предметов, развивать мышление, память, внимание, расширять кругозор, способствовать укреплению веры в свои способности каждого учащегося.
Оборудование: мультимедийное оборудование, раздаточный материал, чистые листы бумаги, фломастер
Ход занятия:
1. Организационный момент.
Тут затеи и задачи!
Игры, шутки- всё для вас!
Пожелаем вам удачи!
За работу, в добрый час!
2. Сообщение темы, целей.
Ребята, сегодня у нас не просто внеклассное занятие по математике. Эта царица наук побывает в гостях у разных учебных предметов, а что из этого получится, вы узнаете позже.
Расскажите , пожалуйста, где вы в жизни сталкиваетесь с математикой? Какие ещё науки , связанные с математикой, вы знаете?
Провести занятие мне помогут герои мультфильма «Смешарики»
3. Разминка.Слайды.
4. Основная часть.
Итак, царица Математика идёт в гости к Литературе. Вспомните сказку «Теремок» (слайд)
А теперь Математика пойдёт в гости к окружающему миру. Октябрь – середина осенней поры. В старину этот месяц называли «листопадом», потому что с деревьев опадают увядшие, пожелтевшие листья
В октябре часто идет холодный мелкий дождь, небо заволакивают серые облака, травы от дождя буреют, цветы вянут. В народе говорят: «От осени к лету поворота нету». По ночам бывают заморозки, и лужи затягиваются корочкой льда. Но характер у этого месяца переменчивый: он и плачет, и смеется. За день погода может измениться несколько раз: то солнышко ярко светит, то дождик надоедливо моросит, а то и первые снежинки запорхают.
Какие пословицы про октябрь можете вспомнить?
Какой по счёту месяц? С помощью 4 палочек выложите число 10.
На урок русского языка .Собрать и разгадать ребусы.(разрезаны на фигуры)
( ПА ,3 Ж И 100 РИЯ КО100ЧКА 3 БУНА 5, НИЦА
) в конвертах . Работа в парах
-Что в конверте?
-Как назвать одним словом?
-Какие фигуры?
А на каком уроке вы пользуетесь красками, цветными карандашами?(уроки изобразительного искусства).
Сейчас мы свами поиграем в цветную игру магический квадрат.
. Чтобы решить следующую логическую задачу, вам нужно проявить смекалку.
Нюше на день рождения подарили три мячика: желтый, зелёный и красный.
Покажите, в каком порядке она может расположить их на полке.
Итак, мы побывали вместе с царицей- Математикой в гостях у разных предметов. Действительно ли математика-главная среди наук?
Что вам сегодня показалось наиболее интересным?
Как вы думаете, нужно проводить такие внеклассные занятия?
А в конце сегодняшнего путешествия я хочу прочитать вам такие стихи
Математика – королева наук!
Без неё не летят корабли.
Даже хлеба не купишь,
Рубля не сочтёшь,
Что по чём не узнаешь,
А узнав, не поймёшь.
Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения!
ГДЗ Математика 2 класс Л.Г.Петерсон Номер 11
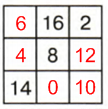
1 квадрат:14 + 8 + 2 = 24 − сумма, которая должна быть в каждой диагонали, строке и столбце:
1 строка: 24 − (16 + 2) = 24 − 18 = 6
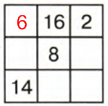
1 столбик: 24 − (14 + 6) = 24 − 20 = 4
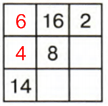
2 столбик: 24 − (16 + 8) = 24 − 24 = 0
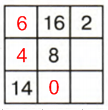
2 строка: 24 − (4 + 8) = 24 − 12 = 12
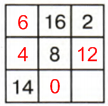
3 строка: 24 − 14 = 10
2 квадрат:
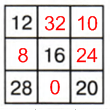
12 + 16 + 20 = 48 − сумма, которая должна быть в каждой диагонали, строке и столбце:
1 столбик: 48 − (28 + 12) = 48 − 40 = 8
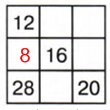
2 строка: 48 − (16 + 8) = 48 − 24 = 24
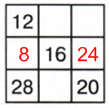
3 строка: 48 − (28 + 20) = 48 − 48 = 0
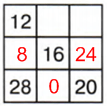
2 столбик: 48 − (16 + 0) = 48 − 16 = 32
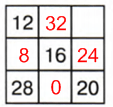
1 строка: 48 − (12 + 32) = 48 − 44 = 4
3 квадрат:
3 + 13 + 11 = 27 − сумма, которая должна быть в каждой диагонали, строке и столбце:
2 строка: 27 − (13 + 5) = 27 − 18 = 9
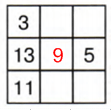
1 диагональ: 27 − (3 + 9) = 27 − 12 = 15
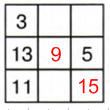
3 строка: 27 − (11 + 15) = 27 − 26 = 1
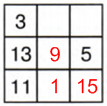
2 столбик: 27 − (1 + 9) = 27 − 10 = 17
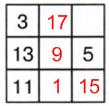
1 строка: 27 − (3 + 17) = 27 − 20 = 7
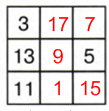
Подписи к слайдам:
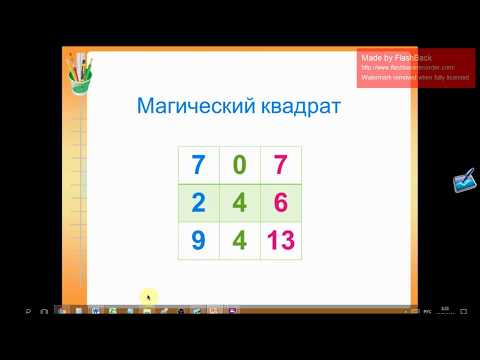
Магический квадрат
2 класс
Из истории магических квадратов
В древнекитайской рукописи Же-Ким (XII — ХІІІ в.в. до н.э.) рассказано предание о том, как император Ию, живший примерно 4000 лет назад, увидел на берегу реки священную черепаху. На панцире черепахи был изображен рисунок из белых и черных кружков: В этом рисунке была найдена удивительная закономерность. Открытие ее произвело столь неизгладимое впечатление, что символ стали считать священным и употреблять при заклинаниях. Назвали его «ло — шу».
В старейшем в мире магическом квадрате китайцев черными кружками изображены четные (женственные) числа, белыми — нечетные (мужественные) числа. В обычной записи он не так эффектен. И все же какой это великолепный образец кросс-сумм, т.е. пересекающихся групп чисел с одинаковыми суммами! Девять порядковых чисел размещены в девяти клетках квадрата так, что суммы чисел вдоль каждой строки, каждого столбца, и каждой из двух диагоналей одинаковы (основное свойство магического квадрата).
В Европу магические квадраты проникли лишь в начале XV века. А в начале XVI века один из них был увековечен выдающимся немецким художником, гравером и немного математиком Альбрехтом Дюрером в его лучшей гравюре «Меланхолия» (1514 г.).
Магический квадрат 4Ч4, изображённый на гравюре Альбрехта Дюрера «Меланхолия», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
Фрагмент гравюры Альбрехта Дюрера «Меланхолия»
Заполняем магические квадраты
4
5
8
6
Ключ — 15
4
9
2
3
5
7
8
1
6
16
2
8
14
Ключ — 24
6
16
2
4
8
12
14
0
10
3
13
5
11
Ключ — 27
3
17
7
13
9
5
11
1
15
13
14
15
10
Ключ — 42
11
18
13
16
14
12
15
10
17
12
16
28
20
Ключ — 48
12
32
4
8
16
24
28
0
20
20
15
25
35
Ключ — 75
20
45
10
15
25
35
40
5
30
МОЛОДЦЫ!!!
 Описание слайда:
Описание слайда:Магический квадрат 2 класс
2 слайд
Из истории магических квадратов В древнекитайской рукописи Же-Ким (XII — ХІІІ в.в. до н.э.) рассказано предание о том, как император Ию, живший примерно 4000 лет назад, увидел на берегу реки священную черепаху. На панцире черепахи был изображен рисунок из белых и черных кружков: В этом рисунке была найдена удивительная закономерность. Открытие ее произвело столь неизгладимое впечатление, что символ стали считать священным и употреблять при заклинаниях. Назвали его «ло — шу».
3 слайд Описание слайда:
Описание слайда:В старейшем в мире магическом квадрате китайцев черными кружками изображены четные (женственные) числа, белыми — нечетные (мужественные) числа. В обычной записи он не так эффектен. И все же какой это великолепный образец кросс-сумм, т.е. пересекающихся групп чисел с одинаковыми суммами! Девять порядковых чисел размещены в девяти клетках квадрата так, что суммы чисел вдоль каждой строки, каждого столбца, и каждой из двух диагоналей одинаковы (основное свойство магического квадрата).
4 слайд Описание слайда:
Описание слайда:В Европу магические квадраты проникли лишь в начале XV века. А в начале XVI века один из них был увековечен выдающимся немецким художником, гравером и немного математиком Альбрехтом Дюрером в его лучшей гравюре «Меланхолия» (1514 г.).
5 слайд Описание слайда:
Описание слайда:Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры (1514). Фрагмент гравюры Альбрехта Дюрера «Меланхолия»
6 слайд Описание слайда:
Описание слайда:Заполняем магические квадраты
7 слайд Описание слайда:
Описание слайда:4 5 8 6
8 слайд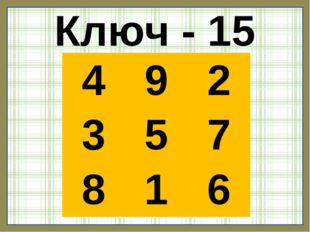 Описание слайда:
Описание слайда:Ключ — 15 4 9 2 3 5 7 8 1 6
9 слайд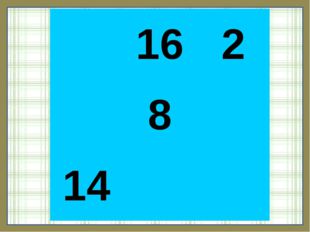 Описание слайда:
Описание слайда:16 2 8 14
10 слайд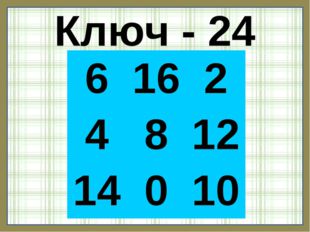 Описание слайда:
Описание слайда:Ключ — 24 6 16 2 4 8 12 14 0 10
11 слайд Описание слайда:
Описание слайда:3 13 5 11
12 слайд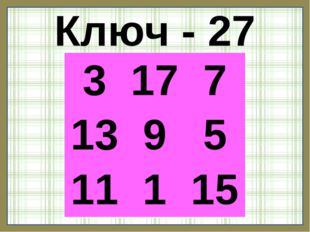 Описание слайда:
Описание слайда:Ключ — 27 3 17 7 13 9 5 11 1 15
13 слайд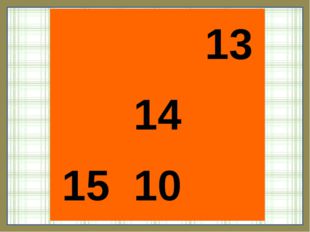 Описание слайда:
Описание слайда:13 14 15 10
14 слайд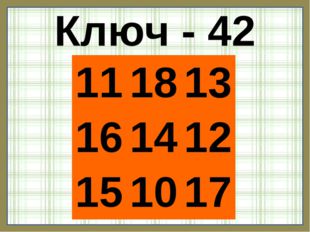 Описание слайда:
Описание слайда:Ключ — 42 11 18 13 16 14 12 15 10 17
15 слайд Описание слайда:
Описание слайда:12 16 28 20
16 слайд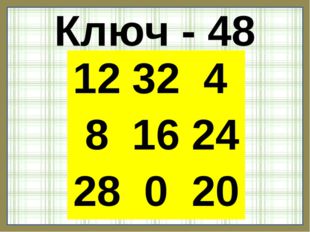 Описание слайда:
Описание слайда:Ключ — 48 12 32 4 8 16 24 28 0 20
17 слайд Описание слайда:
Описание слайда:20 15 25 35
18 слайд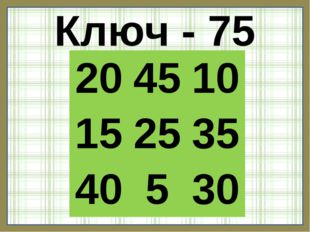 Описание слайда:
Описание слайда:Ключ — 75 20 45 10 15 25 35 40 5 30
19 слайд Описание слайда:
Описание слайда:МОЛОДЦЫ!!!

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-431075
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Конспект занятия по внеурочной деятельности «Занимательная математика» учителя начальных классов Хмельницкой И.В. МБОУ «Школа-лицей № 2»
для 3-В класса
Занятие №11
Тема. Магические фокусы. Игра «Магические квадраты».
Дата:
Цели: познакомить учащихся с магическими фокусами и магическими квадратами, правилами построения логических рассуждений для решения подобных головоломок; формировать способность вычленять необходимые, существенные признаки объекта или процесса через абстрагирование от остальных, несущественных; развивать логическое мышление, активизировать внимание; закрепить навыки устного счёта; воспитывать интерес к урокам математики.
Планируемые результаты: учащиеся научатся определять является ли квадрат магическим, или нет, строить логические рассуждения; получат возможность научиться вычленять существенные признаки, отсекая несущественные.
Ход занятия
I. Организационный момент
– Ребята, знаете ли вы, что магические квадраты занимают воображение математиков уже более двух тысячелетий. Самый первый магический квадрат третьего порядка был известен ещё древним китайцам (ок. 2200 лет до н.э.). Из Китая магические квадраты проникли в Индию (примерно в XI веке), а затем в Японию. В Европу магические квадраты были завезены из Византии в XV веке. Первым квадратом четвёртого порядка, который придумал европеец, считается квадрат А. Дюрера. Дюрер поместил магический квадрат на своей знаменитой гравюре “Меланхолия” (слайд 2). Интересно отметить, что дата создания гравюры (1514 г.) указана числами, стоящими в двух центральных клетках нижней строки.
В средние века магические квадраты связывали с астрологией. Каждой планете соответствовал свой магический квадрат. Считалось, что магические квадраты обладают мистическими свойствами.
В XIX и XX вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Сейчас магические квадраты перестали быть только объектом математических развлечений и очень изящной головоломкой. Магические квадраты находят практическое применение. В последнее время в Интернете появились сообщения об использовании магических квадратов в новейших технологиях создания цифровых изображений.
II. Актуализация опорных знаний и самоопределение к деятельности
Магический квадрат – это квадратная матрица (таблица чисел), в которой суммы чисел вдоль любой строки, любого столбца и любой из двух диагоналей равны одному и тому же числу.
III. Разминка
разгадать их. Я уверена, что у каждого из Вас получится!
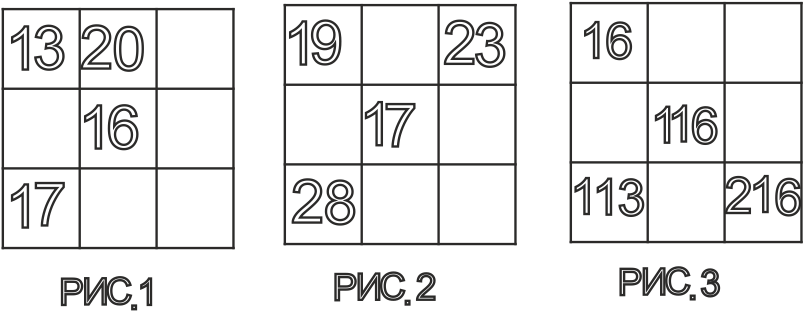
диагоналей равна 48.
IV. Магический фокус. Создание проблемной ситуации.
Совершенно иной тип магического квадрата изображен на следующем рисунке (слайд 4): 
На первый взгляд может показаться, что он составлен без всякой системы и числа в нем расположены случайным образом. Тем не менее этот квадрат обладает магическим свойством, вызывающим удивление не только у человека, далекого от науки, но и у профессионала-математика.
Это свойство лучше всего демонстрировать с помощью пяти монет и 20 бумажных фишек. Попросите кого-нибудь выбрать любое из чисел, вписанных в клетки квадрата. Положите на это число монету и закройте фишками все остальные числа, стоящие в одной строке и одном ряду с выбранным.
Попросите теперь того же человека выбрать любое из чисел, вписанных в незакрытые еще клетки, положите на выбранное число другую монету, а числа, стоящие в той же строке и в том же столбце, что и выбранное во второй раз число, снова закройте фишками. Повторив эту процедуру еще два раза, вы обнаружите, что незакрытой осталась лишь одна клетка. Положите на эту клетку пятую монету.
Если теперь вычислить сумму чисел, накрытых монетами, то она будет равна 57. Это не случайно: сколько бы вы ни повторяли эксперимент, сумма всегда будет одной и той же.
Если вы любите решать математические головоломки, то можете попытаться самостоятельно раскрыть секрет удивительного квадрата. Если у Вас не получится, то не расстраивайтесь. У Вас есть возможность прочитать секрет фокуса с матрицами.
Этот фокус, как и многие другие, после объяснения оказывается до смешного простым. Квадрат представляет собой не что иное, как самую обычную таблицу сложения, правда, составленную весьма замысловатым образом. https://math-around.ru/view_post.php?id=13
V. Весёлая переменка
– Перед новыми заданиями немного отдохнём.
Утром бабочка проснулась, (протираем глазки)
Потянулась, улыбнулась. (Из положения упор присев постепенно выпрямляем туловище, руки вперёд, вверх.)
Раз – росой она умылась, (умываемся)
Два – изящно покружилась, (кружимся на месте)
Три – нагнулась и присела,
На четыре – полетела. (машем руками, как крыльями)
У цветка остановилась, (присели)
Над цветочком закружилась.
VI. Рефлексия
– Понравилось вам работать с магическими квадратами? Почему? Хотите проверить свои умения на прочность? Тогда попробуйте самостоятельно определить: магический данный квадрат или нет.
(слайд 5)
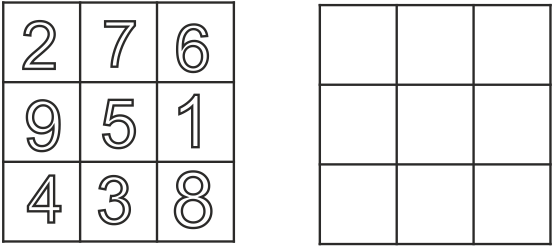
Квадрат, изображенный на рисунке слева – МАГИЧЕСКИЙ КВАДРАТ. Все суммы равны 15.
– Ну, а теперь высший пилотаж! Попытайтесь разместить цифры от 1 до 9 на рисунке справа так, чтобы все эти суммы были различны.
Ответ:
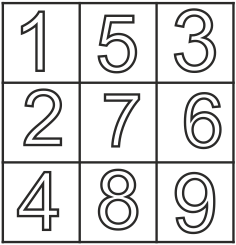
– Молодцы! На следующем занятии мы продолжим развивать свое умение разгадывать магические квадраты..
Магические квадраты. Урок 129. Математика 2 класс
Для просмотра онлайн кликните на видео ⤵
что такое магический квадрат Подробнее

Математика . Урок№ 129 -130. Решение логических задач Подробнее

магические квадраты Подробнее

Что такое Маги́ческий, или волше́бный квадра́т Magic, or the magic square Подробнее

Математика. 2 класс. Волшебный квадрат. Компоненты при сложении. Ким Е.О., учитель начальных классов Подробнее

«Волшебный» квадрат с разными числами Подробнее
Как решать магический квадрат Подробнее
2 класс. Математика: Решение логических задач. 14.05.2020 Подробнее

Волшебный квадрат Подробнее

Магический квадрат 3×3 с разными числами. Решение логической задачи Подробнее

Учимся решать МАГИЧЕСКИЙ КВАДРАТ!!!🤗 Подробнее

Жамбылский район математика 2кл урок 129 Решение логических задач учитель Маханова А К Подробнее

Сенсация! Магические квадраты по совершенной методике (мастер-класс) Подробнее

Как решать магический квадрат Подробнее
2 класс. Математика. Путешествие на речку. Решение логических задач. 15.05.2020 Подробнее

Решение логических задач Подробнее
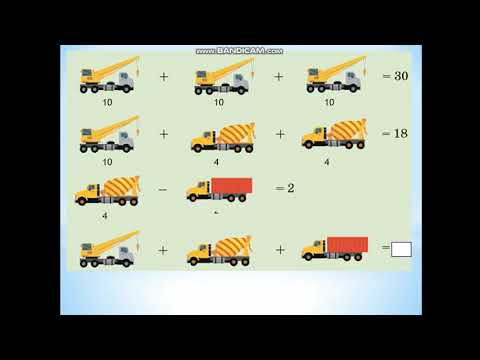
Русский язык. 2 класс. Урок 129. Подробнее
Магический Квадрат
Логические головоломки Волшебные квадратыВолшебные квадраты — это одна из самых простых форм логических головоломок и отличное введение в методы решения проблем, выходящие за рамки традиционных арифметических алгоритмов. Каждый квадрат разделен на ячейки, и правила требуют, чтобы сумма любой строки, столбца или диагонали в квадрате была одинаковой. Учитывая магический квадрат с пустыми ячейками, ваша задача состоит в том, чтобы решить головоломку, предоставив недостающие числа. На этой странице есть рабочие листы с магическим квадратом 3×3, 4×4 и 5×5, которые помогут вам подготовиться к другим задачам, таким как печатные головоломки судоку и многое другое!
3×3 Пазлы с магическими квадратами
16 Пазлы с магическими квадратами
Магические квадраты 3х3 на этих листах-головоломках представляют собой наименее сложную форму магических квадратов, которую вы можете решить.Существуют нормальные версии (с номерами 1-9) и ненормальные версии, которые выдают другое «магическое число» при решении. Дайте им попробовать, прежде чем переходить к магическим квадратам 4х4!
3×3 Магический квадрат
4×4 Пазлы магического квадрата
48 Пазлы магического квадрата
Эти более сложные магические квадраты 4×4 находятся на шаг выше по сравнению с головоломками 3×3, но решить их довольно просто, если вы практиковали свои дополнительные листы. Нормальные квадраты со значениями 1-16 легко решить, но ненормальные квадраты могут нуждаться в вашем калькуляторе!
4×4 Магический квадрат
5×5 Пазлы магического квадрата
48 Головоломки магического квадрата
Обычные магические квадраты 5×5 имеют числа от 1-25 и могут быть настоящим обманщиком мозга.Нестандартные версии головоломок 5х5 — отличное упражнение для детей (или взрослых!), У которых есть солидные навыки решения проблем.
5×5 Магический квадрат
.Март 2006
Что такое магический квадрат?
Существует древняя китайская легенда, которая звучит примерно так. Примерно три тысячи лет назад в Китае произошло большое наводнение. Чтобы успокоить раздраженного бога реки, люди сделали подношение реке Ло, но он не мог быть умиротворен. Каждый раз, когда они приносили жертву, из реки появлялась черепаха. Однажды мальчик заметил следы на спине черепахи, которые, казалось, представляли цифры от 1 до 9.Числа были расположены таким образом, что каждая строка складывалась до 15. Следовательно, люди понимали, что их предложение было неправильной суммой.

Нимфа реки Ло , рисунок тушью на ручном свитке, династия Мин, 16 век. Галерея искусств Freer
Маркировка на задней части черепахи была фактически волшебным квадратом. Магический квадрат — это квадратная сетка, заполненная числами таким образом, что каждая строка, каждый столбец и две диагонали складываются в одно число.Вот как бы выглядел волшебный квадрат из Ло Шу. Он имеет три строки и три столбца, и если вы сложите числа в любой строке, столбце или диагонали, вы всегда получите 15.
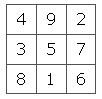
Магический квадрат Ло Шу

Математические свойства
Когда математики говорят о магических квадратах, они часто говорят о порядке квадратов. Это просто количество строк или столбцов, которые есть у магического квадрата. Например, магический квадрат 3 на 3 имеет три строки и три столбца, поэтому его порядок равен 3.
В типичном магическом квадрате вы начинаете с 1, а затем проходите все числа по одному. Например, магический квадрат порядка 3 содержит все числа от 1 до 9, а квадрат порядка 4 содержит числа от 1 до 16. Не удивительно, что магические квадраты, созданные таким образом, называются обычными магическими квадратами.
В магическом квадрате Ло Шу, который является нормальным магическим квадратом, все строки, все столбцы и две диагонали складываются в одно число 15. Мы называем это число магической константой , и есть простая формула Вы можете использовать для определения магической константы для любого нормального магического квадрата.Для магического квадрата порядка n магическая постоянная равна
Итак, для квадрата порядка 3 имеем
M (3) = 3 (3 2 +1) / 2 = 15
Легко получить эту формулу: магический квадрат порядка n имеет ровно n строк, и каждый ряд складывается из магической константы M (n) . Таким образом, нМ (н) — это значение, которое вы получаете, когда складываете все записи в квадрате. Но поскольку каждое число от 1 до n 2 появляется ровно один раз в квадрате, вы знаете, что общее число также равно
1 + 2 + 3 +… + n 2 .
И, как многие из вас могут знать, эта сумма равна n 2 (n 2 +1) / 2 . Собрав все это вместе, вы получите
нМ (n) = n 2 (n 2 +1) / 2,
поэтому
M (n) = n (n 2 +1) / 2.
Оказывается, нормальные магические квадраты существуют для всех порядков, кроме порядка 2. Есть только один магический квадрат порядка 1, и это не особенно интересно: один квадрат с номером 1 внутри! Вы можете сами решить, почему квадрат порядка 2 не существует.Математики обычно считают два магических квадрата одинаковыми, если вы можете получить один из другого с помощью вращения или отражение. Таким образом, существует только один магический квадрат порядка 3, который является магическим квадратом Ло Шу, показанным выше. Существует 880 различных магических квадратов порядка 4 и 275 305 224 порядка 5. Никто не знает, сколько существует магических квадратов порядка 6, но, по оценкам, их число превышает миллион миллионов!
Де Ла Лубере и сиамский метод
Теперь вы можете задаться вопросом, есть ли простой способ создать магический квадрат, не прибегая к догадкам.К счастью, есть. Де Ла Лобер был французским послом в Сиаме (ныне Таиланд) в конце семнадцатого века. По возвращении во Францию он привел с собой метод построения магических квадратов с нечетным числом строк и столбцов, иначе называемых квадратами нечетного порядок.
Начните с поиска средней ячейки в верхнем ряду магического квадрата и запишите в нем число 1. Продолжайте писать числа 2, 3, 4 и т. Д., Каждая из которых находится в соседней по диагонали ячейке к северо-востоку от ранее заполненной ячейки.Когда вы дойдете до края квадрата, продолжайте движение с противоположного края, как если бы противоположные края были склеены. Если вы столкнулись с ячейкой, которая уже заполнена, перейдите к ячейка сразу под ячейкой, которую вы только что заполнили, и продолжайте как прежде.
Когда все ячейки заполнены, две основные диагонали, а также все строки и столбцы должны складываться в одно и то же число, как по волшебству!
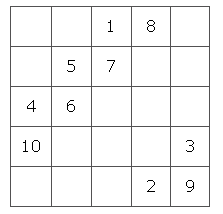
Вот частичная конструкция магического квадрата 5 на 5. Начиная с 1, я заполнил цифры до 10.К северо-востоку от 1 места нет, поэтому я поставил 2 в нижнем ряду, а затем 3. Снова, поскольку 3 находится на краю, 4 идет на противоположной стороне. 6 должно идти в ячейке, где 1, но, поскольку эта ячейка занята, я помещаю 6 сразу под 5 и продолжал до 10. Попробуйте заполнить квадрат, а затем попробуйте сделать некоторые свои.
Хотя этот метод, известный как сиамский метод , является, вероятно, наилучшим известным методом для создания магических квадратов, существуют и другие методы.Немецкий школьный учитель Иоганн Фолхабер опубликовал метод, аналогичный сиамскому, до того, как он был обнаружен де Ле Лобером. Другой способ — метод Лозенга Джона Хортон Конвей, плодовитый британский математик. Доказать, что эти методы работают, можно с помощью алгебры, но это не просто!
Магические квадраты четного порядка
Хотя сиамский метод можно использовать для создания магического квадрата для любого нечетного числа, не существует простого метода, который работал бы для всех магических квадратов четного порядка.К счастью, есть хороший метод, который мы можем использовать, если порядок квадрата равен четному числу, кратному 4. (Для тех, кто заинтересован, метод LUX был изобретен Дж. Х. Конвеем для работы с четными числами, которые не являются делится на 4).
Вместо того, чтобы говорить «числа, которые делятся на 4», математики обычно говорят «числа вида 4k ». Например, 12 имеет форму 4k , потому что вы можете заменить k на 3. Используя ту же идею, числа, которые дают остаток от 2, когда вы делите их на 4, могут называться числами вида 4k + 2
Итак, начните с выбора порядка квадрата, убедившись, что он имеет форму 4k , и пронумеруйте ячейки от 1 до (4k) 2 , начиная с верхнего левого угла и работая вдоль рядов. Затем разделите квадрат на 4 на 4 квадрата и отметьте числа, которые лежат на главных диагоналях каждого квадрата. В примере это цветные цифры; порядок квадрата 4, поэтому единственный квадрат 4 на 4 — это сам квадрат.
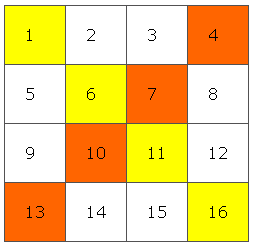
Теперь поменяйте номер с наименьшей маркировкой на номер с наивысшей отметкой, второй номер с наименьшей отметкой на номер с наивысшей отметкой и т. Д.Другой способ сказать, что если магический квадрат имеет порядок n , поменяйте местами числа, которые складываются до n 2 + 1 . В этом конкретном примере порядок равен 4, поэтому мы должны поменять местами числа, которые в сумме составляют 17: 1 и 16, 4 и 13, 6 и 11, 7 и 10.
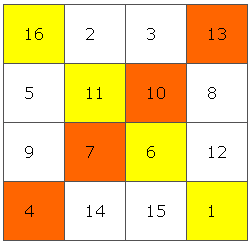
Если вы перевернете этот магический квадрат, он будет идентичен тому, который нарисовал известный немецкий художник Альбрехт Дюрер. Вы можете видеть это в углу его гравюры Melencolia .
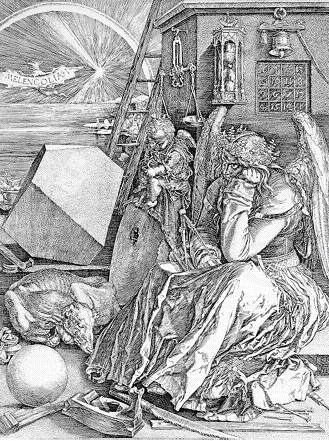
Альбрехт Дюрер, гравюра 1514 Меленколия .

Магический квадрат, появившийся в Melencolia , показанный крупным планом.
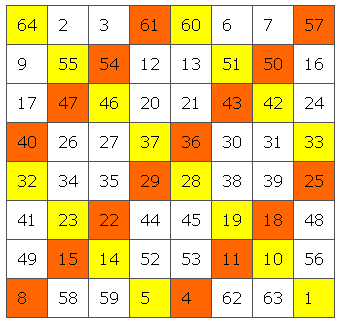
Вот пример магического квадрата 8 на 8, построенного тем же способом. Квадрат был разделен на четыре квадрата 4 на 4, и диагонали были раскрашены. Цветные числа, которые составляют до 65, были переключены: 1 был заменен на 64, 4 был заменен на 61, и так далее.
История рыцаря
Как знает любой шахматист, магический квадрат порядка 8 имеет столько же клеток, сколько и шахматная доска.Это сходство означает, что мы можем создать специальный тип магического квадрата на основе ходов шахматной фигуры.
Рыцарь — интересная фигура, потому что, в отличие от других фигур, он не движется вертикально, горизонтально или по диагонали вдоль прямой линии. Вместо этого конь движется в форме буквы L, как показано на схеме. Но может ли рыцарь, который движется таким образом, посетить каждую клетку на шахматной доске ровно один раз?
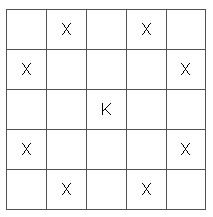
Рыцарь (K) может двигаться в форме буквы L к любому из квадратов, отмеченных X
Одним из первых математиков, исследовавших экскурсию рыцаря, когда проблема стала известна, был великий швейцарский математик Леонард Эйлер.Его работа вдохновила других принять вызов.
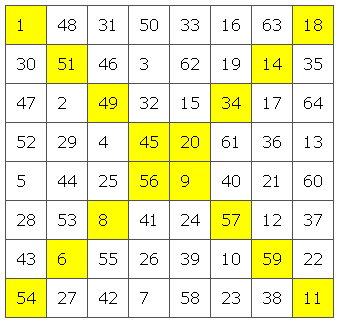
Используя концепцию рыцарского тура, Уильяму Беверли удалось создать магический квадрат, как показано ниже. Клетки нумеруются по порядку, так как их посещает рыцарь. Хотя количество строк и столбцов в сумме составляет 260, главных диагоналей нет, так что, строго говоря, это полумагнитный квадрат. На самом деле, магический квадрат, основанный на экскурсии рыцаря, часто называется волшебным туром, поэтому то, что Беверли продюсировала в 1848 году, — это полумагический тур!
На первый взгляд кажется, что следующий магический квадрат Фейштамеля отвечает всем требованиям.Строки, столбцы и диагонали в сумме равны 260. К сожалению, это только частичный рыцарский тур, поскольку есть скачок с 32 до 33.
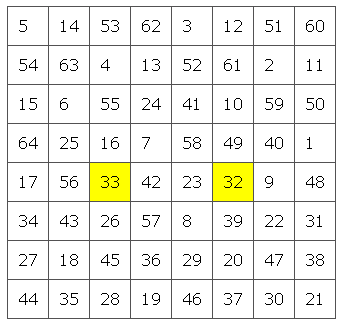
Так когда же можно превратить рыцарский тур в волшебный квадрат? В 2003 году Stertenbrink и Meyrignac наконец решили эту проблему, вычислив каждую возможную комбинацию. Они нашли 140 полумагических туров, но никаких волшебных туров. Мат!
латинских квадратов
Латинские квадраты — настоящие предки Судоку. Вы можете найти примеры латинских квадратов в арабской литературе старше 700 лет.Они были обнаружены Эйлером несколько веков спустя, который рассматривал их как магический квадрат нового типа, и именно благодаря ему мы называем их латинскими квадратами.
Латинские квадраты — это сетки, заполненные цифрами, буквами или символами таким образом, что ни одно число не появляется дважды в одной строке или столбце. Разница между магическим квадратом и латинским квадратом заключается в количестве используемых символов. Например, в магическом квадрате 4 на 4 есть 16 разных чисел, но вам нужно только 4 разных числа или буквы, чтобы получить латинский квадрат 4 на 4.
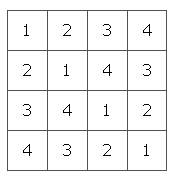
Вот пример латинского квадрата с номерами от 1 до 4 в каждой строке и столбце. Если вы посмотрите на первую строку и первый столбец, вы заметите, что числа встречаются в последовательности: 1, 2, 3, 4. Когда это происходит, мы говорим, что латинский квадрат находится в стандартной форме, или нормализованы. Любой латинский квадрат можно превратить в стандартную форму, поменяв местами пары строк и пары колонны.
Существует только один нормализованный латинский квадрат порядка 3, и есть только 4 различных квадрата порядка 4, но ошеломляющие 377 597 570 964 258 816 порядка 9.В 1979 году Дж. Р. Нечватал разработал сложную формулу, дающую число различных нормированных латинских квадратов любого порядка. До сегодняшнего дня никто из этой или любой другой формулы не мог определить, насколько быстро растет это число по мере того, как площади становится большим.
Если мы объединим два латинских квадрата ниже, мы получим новый квадрат с парами букв и цифр. Пара не повторяется, но сетка содержит каждую комбинацию. Мы называем этот новый квадрат Эйлер-квадрат или Греко-латинский квадрат , и два квадрата, которые образовали квадрат Эйлера, называются взаимно ортогональными .Латинские квадраты и квадраты Эйлера находят широкое применение в математике и за ее пределами, в том числе для проведения экспериментов и организации турниров с круговым циклом. Например, предположим, что ученый Альберт хочет испытать четыре разных препарата (называемых A, B, C и D) на четырех добровольцах. Чтобы сделать это честным тестом, он решает, что каждый волонтер должен пройти тестирование с принимать лекарства каждую неделю, но двум добровольцам не разрешается принимать одно и то же лекарство одновременно. Сказав, что каждая строка представляет отдельного добровольца, а каждый столбец представляет отдельную неделю, Альберт может спланировать весь эксперимент, используя латинский квадрат.
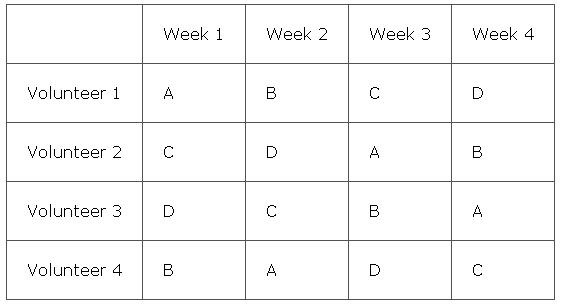
Задача тридцать шесть офицеров
Эйлер проделал значительную работу над латинскими квадратами и даже придумал некоторые методы их построения. Эйлер легко нашел методы построения греко-латинских квадратов и квадратов нечетного порядка, для которых порядок кратен 4, но он не смог получить греко-латинский квадрат порядка 6.
Он даже поставил известную проблему, которую можно решить, только сделав греко-латинский квадрат порядка 6. Задача из 36 офицеров выглядит следующим образом: возможно ли организовать шесть полков, каждый из которых состоит из шести офицеров разных рангов, таким образом, чтобы ни в одной строке или столбце не было двух или более офицеров из одного и того же полка или с одинаковым званием?
Эйлер никогда не решал эту проблему.На самом деле он считал, что невозможно создать греко-латинский квадрат, если порядок имеет вид 4k + 2.
Чуть более ста лет назад предсказание Эйлера частично подтвердилось. Французский математик по имени Гастон Тарри проверил каждую возможную комбинацию для квадрата Эйлера 6 на 6 и показал, что ее не существует.
Наконец, в 1960 году Бозе, Шриханде и Паркеру удалось доказать, что квадраты Эйлера существуют для всех заказов, кроме 2 и 6. Но, учитывая, что в их распоряжении были компьютеры, жаль Тарри, которому пришлось делать все вручную!

Леонард Эйлер
Судоку
Если вы сядете на поезд в Лондоне, вы увидите множество пассажиров с ручкой в руках, газетой на коленях и одной вещью на уме — судоку.
Судоку или Су Доку — это особый тип латинских квадратов. Обычно это сетки 9 на 9, разбитые на 9 меньших по 3 на 3 коробки. Цель игры — заполнить каждую ячейку одним из чисел от 1 до 9, чтобы каждое число появлялось ровно один раз в каждой строке, столбце и поле 3 на 3. Чтобы помочь вам завершить головоломку, несколько чисел уже приведены в качестве подсказок.
Человек, которому приписывают изобретение судоку, — Говард Гарнс. Первая головоломка появилась в журнале Dell Dell в 1979 году и называлась Number Place .Загадка приобрела популярность в Японии в 1980-х годах и была подхвачена в 2004 году британской газетой The Times . Судоку — это японский номер с одним номером , и теперь его имя зарегистрированная торговая марка японской компании-издателя пазлов.
Трудно сказать, сколько существует различных завершенных сеток Судоку, но математики Бертрам Фельгенхауэр и Фрэзер Джарвис использовали исчерпывающий компьютерный поиск, чтобы найти число 6 670 903 752 021 072 936 960, что позже было подтверждено Эдом Расселом.
Решение судоку требует логического мышления и системного подхода. Как правило, достаточно много чисел даны в качестве подсказок в исходной сетке — той, с которой вы начинаете головоломку — чтобы гарантировать, что существует только одно решение. Чем больше чисел заполнено изначально, тем легче становится головоломка. Так что настоящие наркоманы судоку, вероятно, предпочитают небольшое количество начальных подсказок. Но что это минимальное количество подсказок, которые нужно дать, чтобы убедиться, что существует ровно одно — и не более — решение? Это хороший вопрос, на который математики до сих пор не смогли ответить, хотя есть веские основания полагать, что число составляет 17.
А что если мы перевернем этот вопрос? Учитывая, что отдельный завершил сетку , сколько существует минимальных начальных сеток, которые имеют эту сетку в качестве решения? Здесь мы имеем в виду те начальные сетки, из которых больше не может быть удалено число, не делая возможным несколько решений. Опять же, математики не знают ответа на этот вопрос.
Но давайте посмотрим, как решить головоломку судоку. Вот тот, который я создал, чтобы проиллюстрировать один из основных методов, известный как сканирование.
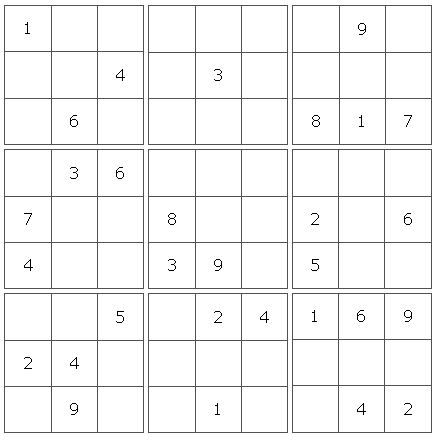
Глядя на средние три ящика, у нас есть 3 в левом ящике и один в среднем, но нам все еще нужно поставить 3 в правом ящике. Так, куда это должно пойти? Ну, это не может идти в верхнем ряду, потому что в этом ряду уже есть 3. По той же причине он не может войти в нижний ряд, который выходит из среднего ряда. В среднем ряду есть только одна свободная ячейка, поэтому 3 Это.
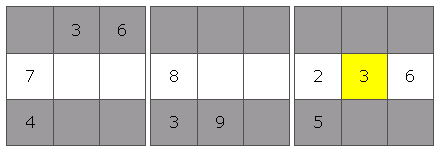
Средние три ящика
Теперь, если мы посмотрим на три нижних поля, одна из строк уже имеет 6 чисел.Я назвал пустые ячейки A, B и C (по порядку слева направо), а пропущенными числами являются 3, 7 и 8. Если вы посмотрите на ячейку C, единственное число, которое может войти в нее, это 7. Это потому, что столбец, в котором находится C, уже содержит 3 и 8.
Найти A и B теперь довольно просто. В той же колонке, что и B, уже есть 3, поэтому B должно быть 8. Это означает, что A должно быть 3. Решение остальной части головоломки немного сложнее, но оно того стоит.
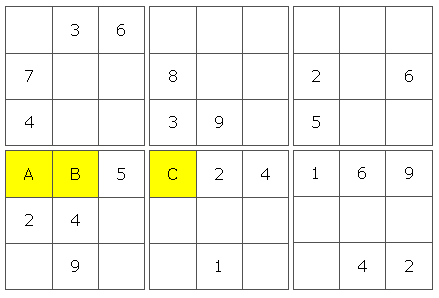
Нижние два ряда
Повальное увлечение судоку охватило весь земной шар, и в нем нет никаких признаков замедления.Из основной темы было разработано несколько вариаций, таких как версии 16 на 16 и комбинации из нескольких сеток (вы можете попробовать дуплексную разницу судоку в головоломке Plus ). Но, как и в случае с магическими и латинскими квадратами, популярность судоку будет зависеть о том, могут ли они продолжать предлагать новые проблемы.
Об авторе
 Хардип Эйден — выпускник математического факультета Имперского колледжа в Лондоне. Помимо математики, он интересуется языками и лингвистикой и в настоящее время изучает японский, французский и британский язык жестов.,
Хардип Эйден — выпускник математического факультета Имперского колледжа в Лондоне. Помимо математики, он интересуется языками и лингвистикой и в настоящее время изучает японский, французский и британский язык жестов., Отложите листы утренней математики и опробуйте некоторые из этих волшебных математических головоломок, которые показывают студентам, как математика может быть очаровательной!
1. Calendar Magic 9
Удивите своих друзей с помощью этого магического трюка умножения из Murderous Maths! Дети говорят другу, чтобы он поставил квадрат в 9 цифр в календаре (коробка 3 х 3). Затем они говорят, что могут быстро найти сумму из 9 чисел в квадрате! Абракадабра и алаказам! Все, что они делают, это умножают число в центре квадрата на 9 и до! У них волшебным образом есть ответ!
2.Shoe Math Magic
Умножьте размер обуви на 5 (должно быть целое число, округлите, если нужно)
Добавьте 50
Умножьте на 20
Добавьте 1015 (измените каждый год / следующий год 1016)
Вычтите год вашего рождения
Первая цифра = размер обуви
Последние 2 цифры = возраст
3. Волшебный квадрат
Волшебный квадрат — это отличная тактильная игра для детей, в которой они переставляют три цифры (горизонтальную, вертикальную и диагональную), так что все они равны одной сумме, магическому числу! Я был вдохновлен Love 2 Learn 2 Day, магический квадрат с молочной крышкой, поэтому я сделал свой собственный! Детям нравится использовать молочные крышки, потому что они могут скользить и скользить по плоской столешнице.Магические квадраты также являются хорошим способом для детей улучшить свои навыки сложения, используя группу слагаемых, три целых числа в уравнении.
4. Магические треугольники по периметру
Магические треугольники по периметру помогают детям улучшить свои навыки сложения, используя три дополнения! Все, что вам нужно, это 6 пробок с надписью 1-6. Дети надевают молочные крышки, образуя треугольник. Их цель состоит в том, чтобы все три стороны складывались в равную сумму.
5.Зубочистка Math Puzzles
Геометрические пазлы с зубочистками, помогающие развить навыки решения проблем и критического мышления.
Список головоломок, которые нужно попробовать:
Puzzle Playground
Planet Seed
Зубочистка Треугольники
6. Искусство в цифрах
Потренируйся в таблицах умножения, создавая бумажные узоры из Sharynideas! Дети определяют шаблоны в своих таблицах умножения. Когда они идентифицируют повторяющийся узор, они создают искусство! Проверьте активность здесь! Кроме того, посетите NRich Math для немного другого способа создания дизайнов из ваших временных таблиц!
7.Пройдите сквозь бумагу
Можете ли вы пройти сквозь отверстие в листе бумаги размером 8,5 × 11 ″? Раздайте всем вашим студентам лист бумаги и посмотрите, смогут ли они выяснить, как вырезать отверстие, достаточно большое, чтобы они могли пройти через него. Тогда покажи им этот волшебный трюк! Посетите Pleacher или The Math Lab для получения инструкций (и бесплатной печати с линиями, чтобы вырезать «идеальное» отверстие)! Затем вытяните свою бумагу и попытайтесь найти область и периметр вашей бумаги! Как это изменилось? Для младших школьников этот проект может быть привязан к базовой единице измерения.Вы даже можете пройти через учетную карточку! Нажмите здесь для подробностей!
8. Головоломки Domino Math
У NRich Math есть множество забавных математических головоломок, которые помогут развить у детей навыки решения проблем. Все, что им нужно, это набор домино! Нажмите здесь для полного списка! Проверьте магические квадраты и прямоугольники домино здесь! Если у вас нет домино, вы можете найти печатные версии онлайн.
Показанное выше:
Умножение Domino
Волшебный квадрат Domino (строки, столбцы и диагонали имеют одинаковую сумму)
Волшебное окно Domino (все стороны равны одной сумме)
9.Квадраты вычитания
Дети выбирают 4 числа (все, что им нравится), чтобы написать в вершинах большего квадрата. Затем они просто вычитают (от угла к углу). Они пишут различия в углах следующего по величине квадрата (где он встречается между линиями) и так далее…
Большой сюрприз — их последний квадрат! Как и в магии, все углы одинаковы! Вывод : Посмотрите, смогут ли дети предсказать, какое будет их загадочное число, прежде чем решать все свои квадраты!
10.X =
Magic Math Trick (x = 2)
1. Подумайте о целом числе от 1 до 10
2. Удвойте его!
3. Добавить 4
4. Разделить на 2
5. Вычесть исходное число
Является ли цифра 2 ?!
Посетите Математическую Лабораторию, чтобы найти алгебру этой математической магии!
Magic Math Trick (x = 18)
1. Выберите число, любое число!
2. Умножьте число на 100.
3. Вычтите исходное число из ответа.
4.Добавьте цифры в своем ответе.
Ваш номер 18 ?!
Пример:
5
5 x 100 = 500
500 — 5 = 495
4 + 9 + 5 = 18
Теперь давайте попробуем большее число!
1,467
1,467 x 100 = 146,700
146,700 — 1,467 = 145,233
1 + 4 + 5 + 2 + 3 + 3 = 18
Это волшебство!
Эрин Биттман — модельер, ставшая учителем. Проверьте ее блог E для изучения!
,