Генератор примеров по математике: NIT for You | Математика: генераторы примеров
Примеры по математике для 1, 2, 3 класса
1-й класс 2-й класс 3-й класс1 класс
В первом классе начинается обучение счёту. Сначала ученикам дают примеры в пределах первой десятки — сложение и вычитание. Когда примеры с однозначными числами решаются уверенно — добавляются примеры с переходом через десяток.
Для тренировки навыков устного счёта удобно воспользоваться генератором примеров:
Примеры на сложение и вычитание в пределах 10
Вычитание однозначных чисел
Примеры на сложение и вычитание в пределах 20
Сложение и вычитание однозначных и двузнычных чисел
Примеры на сложение и вычитание в пределах 100
Сложение и вычитание двузначных чисел
2 класс
Во втором классе изучают таблицу умножения, постепенно проходя каждую цифру доводят навыки умножение для автоматизма.
Для лучшего запоминания рекомендутся давать много разнообразных примеров вперемешку. В это поможет генератор примеров на умножение:
Примеры на умножение однозначных чисел
Сумма не превышает 10
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Помимо умножения во втором классе появляются примеры с пропусками значений — прообраз уравнений с одним неизвестным. В примерах с пропусками значений сначала необходимо правильно подобрать математическое действие, и только потом можно решить пример. Довести навыки счёта до автоматизмав поможет генератор примеров с пропусками значений.
Примеры на сложение и вычитание с пропусками двузначных и однозначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками двузначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Более слодные примеры — неравенства, где для решения нужно вычислить значения в левой и правой части. Это усложнённый вариант обычных примеров.
Это усложнённый вариант обычных примеров.
Неравенства с примерами с однозначными числами
Сумма не превышает 10
Неравенства с примерами с двузначными числами
Сумма не превышает 10
3 класс
В третьем классе продолжается отработка навыков счёта. Примеры становятся более сложными, и для их решения применяется решение в столбик. Для развития навыков быстрого счёта рекомендутся давать ученику большое количество разнообразных примеров. Их можно взять здесь:
Примеры на сложение и вычитание в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Примеры на сложение и вычитание в пределах 10000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 10000
Сложение двузначных чисел с суммой не превышащей 10000
Примеры на умножение в третьем классе включают уже двузначные числа. Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Примеры на умножение опорных чисел «12», «15», «25», «75», «125»
Сумма не превышает 10
| № | Счет в пределах 10 | Пример | Кол |
| 1.01 | Сложение и вычитание в пределах 10 | 3 + 4 = | |
| 1.02 | Состав чисел первого десятка | 5 это 2 и
| |
| 1.03 | Пример с двумя действиями в пределах 10-ти | 8 — 5 + 2 = | |
1. 04 04 | Нахождение неизвестного числа в пределах 10-ти | 5 + = 9 | |
| 1.05 | Сравнение чисел в пределах 10-ти | 4 3 | |
| 1.06 | Сравнение с вычислением в пределах 10-ти | 3 + 5 9 | |
| 1.07 | Задача на вычисление. У Кати 2 косички, а у Маши на 4 больше. Сколько у Маши косичек? | 2 + 4 = | |
| № | Счет в пределах 20 | Пример | Кол |
| 1.08 | Счет в пределах 20 без перехода через десяток, где одно число от 10 до 20, а другое от 0 до 9 | 17 — 3 = | |
| 1.09 | Сложение и вычитание в пределах 20 | 19 — 11 = | |
| 1.10 | Состав чисел в пределах 20-ти | 17 это 11 и
| |
1. 11 11 | Пример с двумя действиями в пределах 20-ти | 17 — 5 + 1 = | |
| 1.12 | Нахождение неизвестного числа в пределах 20-ти | 15 + = 19 | |
| 1.13 | Сравнение чисел в пределах 20-ти | 8 13 | |
| 1.14 | Сложение и вычитание мер длинны (см и дм) в пределах 20-ти без перехода | 2дм 4см + 3дм 5см | |
| 1.15 | Сравнение с вычислением в пределах 20-ти | 8 + 7 14 |
Сложение и вычитание в пределах 100
Описание
Сложение и вычитание в пределах 100 – это примеры, с которых начинается совершенствование навыков счета у ребенка. Практика счета таких примеров поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день. Программа будет полезна ученикам 1-2 классов.
Программа представляет собой тренажер для счета в пределах 100. Она написана в Excel с помощью макросов. С помощью генератора примеров можно создать и распечатать готовые примеры в пределах 100 на нахождение суммы и разности.
Формируются примеры: 4 столбика по 23 примера на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. Для ответов есть клеточки, которые позволяют ребенку тренировать не только устный счет, но и правильное написание цифр.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Другие программы, которые помогут закрепить навыки счета в пределах 100:Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.
На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Генератор простых арифметических примеров для чайников и не только / Хабр
Привет!В этой «статье», а вернее сказать очерке, покажу очень простой способ развлечься зная самые основы latex и python.
Зачем?
Ну, можно генерировать простые выражения для детей чтобы считали.
 Или просто так. Да хоть на обои поставить, если вы такой же фанатик, как и я.
Или просто так. Да хоть на обои поставить, если вы такой же фанатик, как и я.Как это по идее должно работать?
Идея действительно очень простая, написать такую программу может абсолютно каждый. Мы хотим сгенерировать выражение, равное некоторому числу n (которое вводит пользователь). Любое число можно заменить на арифметическое выражение, например, 3 = 1 + 2. А 2 это 4 / 2. Вот так мы сгенерировали 3 = 1 + 4/2. Аналогично, мы введем несколько разных операций и завернем это в LaTeX, язык формул.
Одна неделя опыта в python и matplotlib. Я серьезно.
Основной механизм
Нам нужно распарсить выражение так, чтобы вытащить оттуда числа. Назовем наш класс как генератор проблем (нам всем его так не хватает!)
import random from math import log import math import sys sys.setrecursionlimit(1000) # Эта магия делает нерабочий код рабочим class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)]
Смысл функции extract_nums в том, чтобы получить n пар чисел (a, b), где a — позиция первого символа, b — позиция последнего + 1.
Например, если мы запустим следующий код:
gen = ProblemGenerator()
print(gen.extract_nums("13+256/355+25"))
Увидим:
[(0, 2), (3, 6), (7, 10), (11, 13)]
То есть это массив tuple. (0, 2) означает, что есть число между 0 (включительно) и 2 (не включительно).

Теперь нам хотелось бы сделать разные операторы, начнем с умножения и суммы. Объявим три функции
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + bimport random from math import log import math import sys sys.setrecursionlimit(1000) # Эта магия делает нерабочий код рабочим class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)]
Суть функции unmin не только в том, чтобы просто преобразовать все аргументы в строки, но и в том, чтобы заключить в скобки какой-то из операндов, если он меньше нуля. К примеру, мы получили числа a=3, b=-4. Если мы напишем
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))a = 3 b = -4 a, b = unmin(a, b)
То a=«3», b=»(-4)»
Ну а остальные функции понятные: __c_sum возвращает строку вида «13 + 4», а __c_mul «13 * 4».
Остается соединить эти две штуки и заменять каждое число в выражении на выражение.
Добавим в ProblemGenerator следующий код:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e[(0, 2), (3, 6), (7, 10), (11, 13)]
complexify принимает какое-то число, а возвращает строку — усложненное выражение. Например, если напишем:
gen = ProblemGenerator()
gen.add_expander(__c_sum)
print(gen.complexify(13))
Получим:
31.2 + (-18.2)
Как работает __rxp__? Мы выбираем позицию случайно числа из выражения (к примеру, если есть выражение «13+35/45», то допустим мы выбрали (3, 5)) и заменяем это число на выражение, равное этому числу.

«13+35/45» — рандомное число (3, 5)
«13+» + «(12 + 23)» + «/45»
«13+(12+23)/45»
Так и работает __rxp__
Ну а randexpr работает совсем просто. Например, если у нас четыре шага, то раскрывать выражение будет так:
13
(5.62 + 7.38)
((20.63 + (-15.01)) + 7.38)
((20.63 + (-(67.5 + (-52.49)))) + 7.38)
((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
Попробуем запустить:
gen = ProblemGenerator()
gen.add_expander(__c_sum)
gen.add_expander(__c_mul)
exp = gen.randexpr(1, 5)
print(exp)
Результат:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
LaTeX
Как ни странно, осталось самое простое. Объявим целый ряд разных операторов LaTeX:
def __l_sum(num):
a = 100 ** (random.random() * 2)
b = num - a
a, b = unmin(a, b)
return a + " + " + b
def __l_div(num):
a = num * (random.random() * 100 + 10)
if a == 0. {" + b + "} i*" + c
{" + b + "} i*" + c
Добавим все функции в gen:
gen = ProblemGenerator()
gen.add_expander(__l_sum) # Сумма двух чисел
gen.add_expander(__l_div) # Дробь
gen.add_expander(__l_pow) # Степень
gen.add_expander(__l_sqrt) # Квадратный корень
gen.add_expander(__l_int) # Определенный интеграл
gen.add_expander(__l_sig) # Оператор сигма
И наконец добавим вывод результата:
import matplotlib.pyplot as plt
plt.axis("off")
latex_expression = gen.randexpr(1, 30) # 30 раз заменяем. Выражение будет равно 1
plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=20)
plt.show()
Вот и всё.Весь код
import random
from math import log
import math
import sys
sys.setrecursionlimit(1000)
class ProblemGenerator:
def extract_nums(self, exp):
symbols = list(exp)
NUM = "1234567890."
for i in range(len(symbols)):
symbols[i] = "N" if symbols[i] in NUM else "T"
begins = []
ends = []
for i in range(len(symbols) - 1):
fn = symbols[i] + symbols[i + 1]
if fn == "TN":
begins. append(i)
elif fn == "NT":
ends.append(i)
if exp[-1] in NUM:
ends.append(len(exp) - 1)
if exp[0] in NUM:
begins = [-1] + begins
return [(x + 1, y + 1) for x, y in zip(begins, ends)]
def __init__(self):
self.funcs = []
def add_expander(self, func):
self.funcs.append(func)
def complexify(self, num):
return random.choice(self.funcs)(num)
def __rxp__(self, exp):
x, y = random.choice(self.extract_nums(exp))
exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:]
return exp
def randexpr(self, ans, steps):
e = str(ans)
for i in range(steps):
e = self.__rxp__(e)
return e
def unmin(*args, acc=2):
r = []
for arg in args:
f = round(arg, acc)
if f > 0:
f = str(f)
else:
f = "(" + str(f) + ")"
r.append(f)
return r
def __c_sum(num):
a = round(random.
append(i)
elif fn == "NT":
ends.append(i)
if exp[-1] in NUM:
ends.append(len(exp) - 1)
if exp[0] in NUM:
begins = [-1] + begins
return [(x + 1, y + 1) for x, y in zip(begins, ends)]
def __init__(self):
self.funcs = []
def add_expander(self, func):
self.funcs.append(func)
def complexify(self, num):
return random.choice(self.funcs)(num)
def __rxp__(self, exp):
x, y = random.choice(self.extract_nums(exp))
exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:]
return exp
def randexpr(self, ans, steps):
e = str(ans)
for i in range(steps):
e = self.__rxp__(e)
return e
def unmin(*args, acc=2):
r = []
for arg in args:
f = round(arg, acc)
if f > 0:
f = str(f)
else:
f = "(" + str(f) + ")"
r.append(f)
return r
def __c_sum(num):
a = round(random. {" + b + "} i*" + c
gen = ProblemGenerator()
gen.add_expander(__l_sum)
gen.add_expander(__l_div)
gen.add_expander(__l_pow)
gen.add_expander(__l_sqrt)
gen.add_expander(__l_int)
gen.add_expander(__l_sig)
import matplotlib.pyplot as plt
plt.axis("off")
latex_expression = gen.randexpr(1, 30) # 30 раз заменяем. Выражение будет равно 1
plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=15)
plt.show()
{" + b + "} i*" + c
gen = ProblemGenerator()
gen.add_expander(__l_sum)
gen.add_expander(__l_div)
gen.add_expander(__l_pow)
gen.add_expander(__l_sqrt)
gen.add_expander(__l_int)
gen.add_expander(__l_sig)
import matplotlib.pyplot as plt
plt.axis("off")
latex_expression = gen.randexpr(1, 30) # 30 раз заменяем. Выражение будет равно 1
plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=15)
plt.show()
Результат (3 скриншота)
Сравнение чисел до 100.
Главная / Генератор примеров по математике.
Наш проект uchik.ru развивается только благодаря средствам от наших посетителей. Если вы хотите видеть у нас какие-либо дополнительные упражнения по математике, напишите их в комментариях.
Поддержи проект, подкинь денег на развитие 💰
На упражнения «четное/нечетное» : Собрано 12р. Надо 500р. Донатить
Приведение к общему знаменателю Донатить
Сложение дробей Донатить
Вычитание дробей Донатить
Умножение дробей Донатить
Деление дробей Донатить
Распечатать. Печатается 2 листа. Первый — задания, Второй — задания с ответами.
Печатается 2 листа. Первый — задания, Второй — задания с ответами.
После решения обязательно проведите проверку !
Задания каждый раз выдаются разные.
Задание
Сравнение чисел до 100.57 ___ 64
51 ___ 5
85 ___ 21
80 ___ 36
2 ___ 95
24 ___ 33
3 ___ 86
39 ___ 17
17 ___ 82
88 ___ 84
68 ___ 69
81 ___ 80
22 ___ 33
4 ___ 90
21 ___ 31
91 ___ 11
27 ___ 82
65 ___ 78
22 ___ 77
7 ___ 30
95 ___ 48
40 ___ 82
63 ___ 52
39 ___ 6
84 ___ 2
97 ___ 33
4 ___ 43
28 ___ 27
75 ___ 24
43 ___ 62
68 ___ 22
32 ___ 84
36 ___ 84
47 ___ 67
14 ___ 38
63 ___ 16
13 ___ 45
99 ___ 99
48 ___ 8
34 ___ 54
43 ___ 23
90 ___ 18
8 ___ 1
91 ___ 9
34 ___ 89
73 ___ 92
31 ___ 65
86 ___ 56
44 ___ 82
61 ___ 85
64 ___ 57
5 ___ 80
72 ___ 11
72 ___ 56
79 ___ 88
14 ___ 79
17 ___ 65
9 ___ 80
78 ___ 62
76 ___ 31
Ответы
Сравнение чисел до 100.
57 51 > 5
85 > 21
80 > 36
2 24 3 39 > 17
17 88 > 84
68 81 > 80
22 4 21 91 > 11
27 65 22 7 95 > 48
40 63 > 52
39 > 6
84 > 2
97 > 33
4 28 > 27
75 > 24
43 68 > 22
32 36 47 14 63 > 16
13 99 = 99
48 > 8
34 43 > 23
90 > 18
8 > 1
91 > 9
34 73 31 86 > 56
44 61 64 > 57
5 72 > 11
72 > 56
79 14 17 9 78 > 62
76 > 31
Генератор заданий для школы онлайн
| Созданные примеры для учащихся |
о генераторе выражений
Данный бот наверняка заинтересует преподавателей, организаторов математических конкурсов и олимпиад. В настоящее время практически на каждый учебник с заданиями есть свой решебник ( с ответами и иногда с подробным решением). Как в таком случае оценить знания ученика?
На мой взгляд самое простое решение, и оно конечно же лежит на поверхности и используется большинством преподавателей, это способность ученика объяснить ход решения заданной задачи.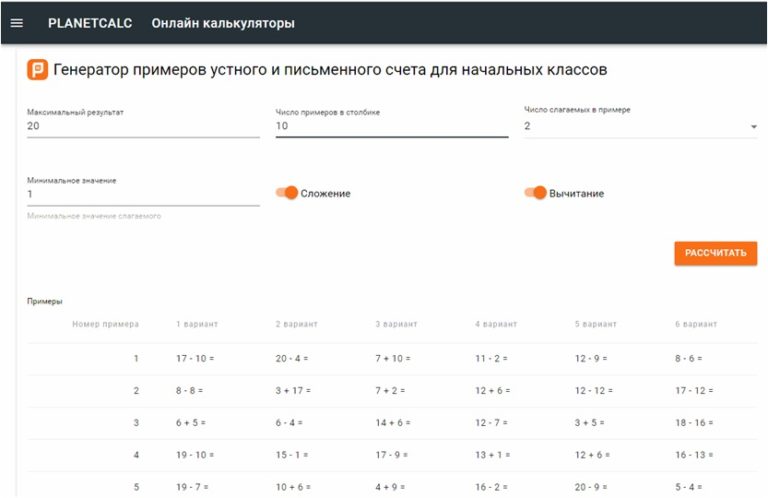 Это неплохо действует на физических задачах, но совсем не действует на решении арифметических задач, где нужно посчитать результат заданного выражения, ничего не доказывая и не объясняя.
Это неплохо действует на физических задачах, но совсем не действует на решении арифметических задач, где нужно посчитать результат заданного выражения, ничего не доказывая и не объясняя.
Пример 2-(4+5)=? или 3*(2-5)+7=?
Задавать подобные примеры на дом, это 100% вероятность что ученик, посчитает это на калькуляторе, на компьютере. Разве этого мы хотим добиться от своих подопечных? Что бы они умели быстро нажимать на клавиатуру? Возможно это и важно, но это не относится никак к разделу математики.
Цель подобных заданий, научить ребенка мыслить, уметь считать в уме.
Чем же наш генератор лучше чем другие?
1. Он планируется как универсальное решение. То есть это база, для создания дальнейших генераторов ( например заданий по высшей алгебре или комплексной арифметики)
2. Он бесплатен.
3. Убраны все возможные ограничения по размеру заданий и сложности.
4. Выражение может содержать скобки.
Конечно же есть и недостатки
— к сожалению скобок в любом выражении будет не больше двух. Но если генератор будет пользоваться спросом, то решим и эту проблему.
Но вернемся к вопросу как же проверить знания ученика при решении задач по арифметики? На наш взгляд самый простой способ это дать сгенерированное задание ученику, который вызван к доске и решает именно там. Такие задания на устный счет, без возможности воспользоваться калькулятором, помогут учителю оценить способности подопечного.
Существует еще другой генератор — Генератор матриц с детерминантом
Синтаксис:
exam разрядность,операнды, количество операндов
разрядность — показывает с какими числами будут создаваться задания. Если 1 то от 1 до 10, если два, то от 1 до 100, если 3, то от 1 до 1000 и так далее
операнды — символы арифметических операций. Если мы генерируем задания для младшего возраста которые умеют только складывать и вычитать, то пишем +- или -+.
Если это средний уровень и ученики умеют уже умножать числа то пишем +-*, а если еще и деление то запишем вот так +-*/
количество операндов — фактически это количество операций в одном задании. Опять же все зависит от уровня тестируемых. Если нам нужно генерировать примеры типа 2+4, 5-8 и так далее то видно что операнд тут один, и значит количество тоже будет равно единице.
А если мы хотим генерировать примеры типа 2*(3-4)+4-7+3/2 то количество операндов будет равно 5
Бот создает 20 заданий в табличной форме, а также в другом столбце дает правильный ответ.
Правильный ответ может содержать как число, так и вид число=число. Такой вид говорит лишь о том, что есть два альтернативных ответа. Самый простой пример это решение с дробями.. где ответ можно выдать как и 0.25, так и 1/4
Это будет очень удобно для сверки ответов, когда ответ должен быть выражен в виде дроби.
Пример
Создадим задания с использованием скобок, с числами от 1 до 10, с используемыми операндами +(плюс) и -(минус), и длиной в 4 элемента.
Делаем вот такой запрос
exam 1,+-,4!
Получаем вот такой ответ ( если используем XMPP клинета)
8-(10-1) = -1 = -1/1
(2+2+2)+6+8 = 20 = 20/1
(10-10)+1+5-4 = 2 = 2/1
(8-4-6+10)-4 = 4 = 4/1
4+1-(7-3)+9 = 10 = 10/1
(7-7-1+6)-3 = 2 = 2/1
(6-4+10-3)+5 = 14 = 14/1
(7+3)-7+9-2 = 10 = 10/1
(5-1+4)-5+6 = 9 = 9/1
1+(4-9-3+3) = -4 = -4/1
10-(1+1+9)-1 = -2 = -2/1
2-(9+9+3)+3 = -16 = -16/1
2-7-(1-8)+1 = 3 = 3/1
(8+2+2)-1-1 = 10 = 10/1
2+9+(1-5+7) = 14 = 14/1
(3-7-8+5)-7 = -14 = -14/1
5-(1+5-2)-6 = -5 = -5/1
(9+6-9-6)-2 = -2 = -2/1
(5-2+7)+9-1 = 18 = 18/1
1-(1+1)+1-10 = -10 = -10/1
Анализируя полученный ответ, мы можем заметить банальные примеры как (2-4+4) или 8+(2-2). Да, есть такое. Объяснение простое, так как у бота нет критерия «установить сложность», а сложность понятие субъективное, то он оперирует только в рамках строго заданных параметров.
Да, есть такое. Объяснение простое, так как у бота нет критерия «установить сложность», а сложность понятие субъективное, то он оперирует только в рамках строго заданных параметров.
Но с другой строны и преподавателю, будет всегда из чего выбрать.
Вот еще один пример, совсем простой для первоклашек
exam 1,+-,1
1+6 = 7 = 7/1
2-6 = -4 = -4/1
3+7 = 10 = 10/1
2-9 = -7 = -7/1
5-5 = 0 = 0/1
4+6 = 10 = 10/1
4-3 = 1 = 1/1
6+1 = 7 = 7/1
5-10 = -5 = -5/1
8+9 = 17 = 17/1
9+7 = 16 = 16/1
5+3 = 8 = 8/1
9-9 = 0 = 0/1
7-2 = 5 = 5/1
1+6 = 7 = 7/1
6-6 = 0 = 0/1
10+4 = 14 = 14/1
2+1 = 3 = 3/1
3-3 = 0 = 0/1
4+8 = 12 = 12/1
Хоть сейчас, копируй печатай и раздавай для расчетов.
А вот более сложный ( с умножением и делением двухзначных чисел)
exam 2,+-/*,4!
(1-24+88/75-63) = -84.826666666667 = 6362/-75
(88/68-11-3/37) = -9.7869634340223 = -6156/629
55/16/98/(99+26) = 0.0002806122449 = 11/39200
82+23+40/(25+59) = 105.47619047619 = 2215/21
(8696*15)*60*32 = 250444800 = /1
43*85/(6220*27) = 0.0217637251399 = 731/33588
(20+67)+73+51/28 = 161.82142857143 = 4531/28
21+(31-98+28)-79 = -97 = -97/1
72+(54-87*26-98) = -2234 = 2234/-1
68+(58/39-85/30) = 66.653846153846 = 1733/26
28/(94-29)*3-31 = -29.707692307692 = 1931/-65
(96*82+11)*93+20 = 733139 = /1
(96/8-34)/61+24 = 23. 639344262295 = 1442/61
639344262295 = 1442/61
75-(28*86)-14/70 = -2333.2 = -11666/5
78-47+(23/81-77) = -45.716049382716 = -3703/81
913*(1+7)-9 = 7295 = 7295/1
95+41*60-(35/17) = 2552.9411764706 = 43400/17
(54*9294*99)+78 = 49685802 = /1
52*24/84-(10+45) = -40.142857142857 = 281/-7
(35*50/20/89) = 0.9831460674158 = 175/178
Как видите ответ может быть в виде числа с точкой, так и предусмотрен альтернативный вывод результата в виде дроби.
Удачных расчетов Вам!
- Генератор матриц с детерминантом >>
РАДУГА: Математика
Сколько всего нужно узнать и выучить ребенку за короткий срок: выучить буквы и цифры, научиться читать, писать, считать и решать.
Притом, что способности у всех деток разные.
Кто-то схватывает все «на лету», кому-то требуется чуть больше времени.
Чтобы закрепить и улучшить начальные навыки счета у детей, на сайте «Быть МАМОЙ» создан онлайн — Генератор, который создает примеры и уравнения по математике для детей дошкольного и младшего школьного возраста.С помощью такого онлайн генератора вы можете абсолютно бесплатно создать, скачать и распечатать готовые примеры на сложение и вычитание, на умножение и деление.
Готовые примеры по математике генерируются на странице в клеточку, что позволяет ребенку тренировать не только устный счет, но и правильное написание цифр.
Генератор примеров и уравнений, имеет внутренние настройки, изменяя которые вы сможете создать примеры для детей разного возраста и уровня подготовки ( от 5 лет до 2-3 класса).
Чтобы получить и распечатать примеры по математике, вам нужно:
1. Задать (выбрать) параметры для заданий
- по количеству примеров: 10, 20, 30, 60 (2листа), 90 (3 листа)
- по виду задания: пример или уравнение
- по функциям математических действий: сложение, вычитание, умножение и деление.

- по диапазону чисел: от 1 до 100 (например — от 5 до 10, от 10 до 50 и т.п.)
2. Распечатать полученый файл. Предварительно вы можете сохранить файл с заданиями на компьютер или флешку.
ГЕНЕРАТОР ПРИМЕРОВ И УРАВНЕНИЙ
* Если вы генерируете примеры в браузере «Firefox», возможно некорректное отображение pdf.файлов в результате генерации (генерируется пустая страница в клеточку, либо нет знаков математических действий)
В этом случае вам нужно:
1. Сохранить полученный (некорректный) документ на компьютер, а затем открыть и распечатать файл с примерами с вашего компьютера.
2. Открыть данную страницу в другом браузере (Chrome, Яндекс), скопировав адрес страницы и вставив его в адресную строку.
Используйте онлайн генератор примеров по математике, если:
— Ваш ребенок только начал изучать счет. Выберите самые начальные параметры для генерации. Чтобы получились самые простые примеры по математике.
Чтобы получились самые простые примеры по математике.
— Вашему ребенку требуется дополнительная подготовка по математике.
— Вы собираетесь в длительную поездку. Решение примеров и уравнений будет полезным занятием, которое поможет скоротать время в дороге.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Благодаря параметрам выбора можно создать сколько угодно заданий разного уровня сложности для подготовки.
Преимущества генератора математических примеров.
— Не нужно заранее покупать задачники и пособия по математике с примерами и уравнениями.
— Чтобы получить примеры для решения, не нужно предварительно скачивать программу на компьютер. Все примеры генерируются онлайн.
— Вы можете скачать файл с примерами на компьютер и распечатать его в любое время.
— Примеры генерируются на странице в клеточку, что очень удобно для правильного написания цифр ребенком.
— Вы можете подобрать задания индивидуально для вашего ребенка в зависимости от его уровня подготовки.
| 9 | LCM (наименьшее общее кратное) | НОК 17 и 4 = | 68 | л · см |
| 10 | НОД (Наибольший общий знаменатель) | НОД 1 и 4 = | 1 | ЖКД |
| 27 | Основная факторизация | Найдите простые множители 173 | [173] | prime_factors |
| 40 | Общие факторы | Общие множители 79 и 64 = | [1] | common_factors |
| 51 | HCF (наивысший общий коэффициент) | HCF из 18 и 1 = | 1 | hcf |
| 55 | Сравнение surds | Заполните пропуски 29 ^ (1/4) _ 91 ^ (1/2) | < | surds_comparison |
| 63 | Процент прибыли или убытка | Процент прибыли при CP = 781 и SP = 878 составляет: | 12. (1/2) = 51.38093031466052 (1/2) = 51.38093031466052 | геометрическое_среднее |
| 68 | Среднее гармоническое значение чисел | Среднее гармоническое из 4 чисел 18, 24, 1, 31 = | 4 / ((1/18) + (1/24) + (1/1) + (1/31)) = 3,5 414518048393493 | гармоническое_среднее |
| 69 | Евклидова норма или L2 норма вектора | Евклидова норма или норма L2 вектора [943.6989301957527, 942.687709334459, 415.08527238528325, 794.7248710456973]: | 1607.206020456812 | euclidian_norm |
| 81 | Цельсия в Фаренгейт | Преобразование 18 градусов Цельсия в градусы Фаренгейта = | 64,4 | по шкале Цельсия |
| 82 | Расчет срока AP | Найдите термин номер 55 ряда AP: 63, 7, -49 … | -2961 | arithmetic_progression_term |
| 83 | Расчет суммы AP | Найдите сумму первых 68 членов ряда AP: -58, 37, 132. .. .. | 212466,0 | arithmetic_progression_sum |
| 85 | Преобразует десятичные числа в римские | Число 2089 римскими цифрами: | .MMLXXXIX | десятичных_значных_цифровых |
| 92 | Комплекс в полярную форму | рексп (итета) = | 7.28эксп (и-1.85) | комплекс_то_полярный |
| 93 | Союз, пересечение, разность двух наборов | Даны два набора a = {2, 3, 4, 5, 8, 9}, b = {9, 5, 6, 7}.Найдите соединение, пересечение, a-b, b-a и симметричную разность | Объединение равно {2, 3, 4, 5, 6, 7, 8, 9}, пересечение равно {9, 5}, ab равно {8, 2, 3, 4}, ba равно {6, 7}, симметрично разница составляет {2, 3, 4, 6, 7, 8} | set_operation |
| 94 | Базовая конверсия | Преобразование DD5D из базы 15 в базу 10. | 46888 | base_conversion |
| 98 | Коэффициент полномочий с одинаковой базой | Частное 49 ^ 2 и 49 ^ 2 = 49 ^ (2-2) = 49 ^ 0 | 1 | quotient_of_power_same_base |
| 99 | Коэффициент способностей при одинаковой мощности | Частное 40 ^ 4 и 39 ^ 4 = (40/39) ^ 4 = 1. 4 4 | 1,1065767400162785 | quotient_of_power_same_power |
| 101 | Високосный год или нет | Год 2037 | год не високосный | is_leap_year |
| 102 | Минута в час преобразование | Преобразование 897 минут в часы и минуты | 14 часов 57 минут | минут_до_ часов |
| 106 | функция знака | знак 650 = | 1 | signum_function |
| 109 | Биномиальное распределение | Производитель металлических поршней считает, что в среднем 30.15% производимых ими поршней отбраковываются из-за неправильного размера. Какова вероятность того, что партия из 17 поршней будет содержать не более 5 забракованных поршней? | 59,15 | binomial_distribution |
| Сложение / вычитание (и умножение) Обычно подходит для 1-го и 2-го классов, поскольку позволяет вводить числа до 100.  Вопросы могут быть горизонтальными или вертикальными (сложенными).Для сложения можно установить максимальную сумму, поэтому вы можете легко работать в пределах 10, 20 или 100. Вопросы могут быть горизонтальными или вертикальными (сложенными).Для сложения можно установить максимальную сумму, поэтому вы можете легко работать в пределах 10, 20 или 100. | Сложение / вычитание (и умножение) Вопросы могут быть представлены с пропущенными дополнениями. например 4 + ___ = 9. Существуют опции для управления диапазоном номеров, а также порядком чисел и пробелов в уравнениях. |
| Поиск пар чисел до 5, 6, 7, 8, 9 или, 10. Формирует числовые квадраты, на которых пары соседних чисел, которые складываются вместе, образуя заданное число, обведены кружком. | Сложение / Вычитание Cuisenaire Жезлоподобные задачи с двумя смежными «стержнями», расположенными над другим, длина которых равна длине обоих «стержней» выше. Можно установить итоговые суммы и управлять положением ответа. Обычно подходит для 1-го класса и позднего детского сада. |
| Сложение / Вычитание Позволяет создавать вопросы на сложение и вычитание и комбинировать их с добавлением / вычитанием нуля, единицы и / или удвоения.  Цифры от 10 до 20 и выше. Цифры от 10 до 20 и выше. | Вычитание Показывает замену десятичной единицы на 10 с блоками разрядных значений наряду с алгоритмическим вычислением. Примечание: это продолжение генератора Decompose a 10 в подразделе Place Value ниже. |
| Сложение / вычитание (большие числа) Уровень 3 и 4 класса. Для сложения и вычитания в пределах 1000, а также для сложения и вычитания с большими многозначными числами (до 999 999). Вопросы могут быть просто сложением, вычитанием или их комбинацией. | Сложение от 2 до 8 слагаемых Позволяет сложить (с вертикальным форматированием) до 8 чисел. Максимальное число может быть от 1 до 6 цифр. |
| Сложение / вычитание с 3 числами Позволяет сложение или вычитание, или их комбинацию с 3 числами (с горизонтальным форматированием). Можно установить максимальное и минимальное количество и общее количество (для добавления). | |
| Умножение и деление | |
| Деление / умножение Полезно при изучении и запоминании математических фактов.  Вопросы могут быть отформатированы по горизонтали или вертикали и могут быть просто делением или могут представлять собой смесь деления и умножения. Вопросы могут быть отформатированы по горизонтали или вертикали и могут быть просто делением или могут представлять собой смесь деления и умножения. | Деление / умножение Устанавливает вопросы с «пропущенными» числами. например __ x 9 = 27, 48 ÷ ___ = 8 |
| Умножение (большие числа) Обычно 3–5 классы. Позволяет умножать многозначные числа с возможностью сделать одно или оба числа кратными 10 или 100. | Длинное деление Диапазон делителей и дивидендов может быть установлен таким образом, чтобы давать несколько типов вопросов деления.например 4 цифры на 1 цифру, 5 цифр на 2 цифры. Существует вариант «без остатка» плюс дополнительные направляющие линии, помогающие выстроить работу. |
| Умножение методом прямоугольников Создает вопросы с 1-значным x 2-значным или 2-значным x 2-значным числом, на которые учащиеся должны ответить, умножая десятки, затем единицы и затем складывая частичные произведения, чтобы получить полный ответ.  | Умножение частичных произведений Продолжает сказанное выше с вариацией формата. На вопросы с 1-значным x 2-значным ответом нужно отдельно умножить десятки и единицы. |
| Дроби | |
| Генератор рабочего листа дробей Вопросы сложения, вычитания, умножения и деления дробей. Могут быть установлены смешанные числа, целые числа, общие знаменатели. | Упрощение дробей Создает дроби, требующие упрощения. Три разных уровня сложности. |
| Генератор неправильных дробей / смешанных чисел Обеспечивает преобразование неправильных дробей в смешанные числа и наоборот.Степень сложности можно контролировать, ограничивая целую числовую часть и / или диапазон знаменателя. | Дробь от целого числа Вопросы формы «4/5 из 25 =». Примеры пользовательских настроек включают в себя только единичные дроби, а ответы — целое число. |
| Десятичные числа | |
| Генератор десятичных знаков Обычно вопросы уровня 5-го класса.  Предоставляет наборы вопросов для сложения, вычитания, сложения и вычитания или умножения с использованием десятых, сотых или тысячных долей. Предоставляет наборы вопросов для сложения, вычитания, сложения и вычитания или умножения с использованием десятых, сотых или тысячных долей. | Десятичные дроби Диапазон чисел и количество десятичных знаков могут быть установлены как для делимого, так и для делителя. |
| Умножение десятичных знаков Можно установить диапазон чисел для обоих чисел. Десятичные дроби могут быть ограничены до десятых, сотых или тысячных. Также можно использовать целые числа, включая числа, кратные 10 и 100. | Округление десятичных дробей Место для округления, чтобы получить целую единицу, десятую, сотую или тысячную как опции или как единственное число. |
| Значение места | |
| Сотни, десятки и единицы Запись числа сотен, десятков и единиц на основе количества блоков разрядных значений, а затем запись полного числа. | Разложить 10 Помогает подготовить учащихся к вычитанию при перегруппировке, обменивая 1 десятку на 10.  например им предлагается увидеть 65 как 5 десятков и 15 единиц. Генератор рабочих таблиц последующего вычитания приведен выше. например им предлагается увидеть 65 как 5 десятков и 15 единиц. Генератор рабочих таблиц последующего вычитания приведен выше. |
| Числа в развернутой форме Запись 7 978 как 7 000 + 900 + 70 + 8. Диапазон номеров может быть равен 99, 999, 9999 и / или 999 999. | |
| Уравнения и выражения | |
| Уравнения Создает четыре различных типа простых уравнений. например 3r = 6, 5t + 4 = 14, 8n / 3 = 16, 3x / 6 — 3 = 27 . Типы могут быть изменены и объединены на каждом листе, а настройки могут быть выполнены для отдельных строк. | Генератор факторинга / раскрытия выражений Предоставляет два типа выражений. например 4x + 40 и 7c + 21d . Рабочие листы могут быть созданы с факторингом или вопросами с расширяющимся выражением. |
| Решение одновременных уравнений Создает вопросы с парами линейных уравнений, которые можно решить, чтобы получить значения x и y.  Обычно это ресурс 8-го класса. Обычно это ресурс 8-го класса. | Quadratic Expressions создает выражения в форме a 2 + 6a + 8 для факторизации.Он допускает три различных уровня сложности, а также включает в себя возможность вопросов по расширяющимся выражениям. |
| Прочие | |
| Генератор рабочих листов для округления чисел № 1 Округление до ближайших 10 и / или 100 | Генератор рабочих листов округления чисел # 2 Округление больших чисел от тысяч до разряда 100 миллионов. |
| Генератор процентной таблицы Предоставляет два типа вопросов: e.г. Что составляет 5% от 20, а 12 — как процент от 40? Количество и процентные диапазоны можно контролировать | Отсутствующие числа Создает последовательности чисел с различными интервалами. Можно установить диапазон номеров, диапазон интервалов, номер для отображения, номер для скрытия и другие параметры.  |
| Циферблаты Создает один циферблат изменяемого размера, для которого можно установить время. Удобно для создания одиночных распечаток. |
Генератор eQuation
Генератор eQuationЛинейные уравненияЛинейное уравнение — это уравнение, в котором каждый член является либо константа или произведение константы на первую степень переменная.Проще говоря, это математическое предложение, в котором вы может видеть только одну букву (которая может встречаться более одного раза), но не будет степеней (в квадрате, кубе и т. д.). Вот пример простое линейное уравнение: 2х + 7 = 15 Это уравнение можно «решить» чтобы найти, какое значение представлено буквой x. Генератор eQuation выше может
составляйте неограниченное количество уравнений, чтобы практиковаться в их решении.Ты можешь
измените параметры так, чтобы один из пяти различных типов уравнения
отображается. Вот примеры, показывающие хороший способ решать уравнения, думая о двух сторонах уравнения как две стороны баланса.Уравнение останется сбалансированным, только если вы делаете одно и то же (умножаете, делите, складываете или вычитаете) с обоими стороны. | ||
Тип 1 \ (3x = 12 \) Проделав то же самое с обеими сторонами уравнения, вы можете найти, чему равен один x. Упражнение для самостоятельной маркировки | Тип 2 \ (4x — 3 = 13 \) Упражнение для самостоятельной маркировки | |
Тип 3 \ (5x + 3 = 3x + 15 \) Упражнение для самостоятельной маркировки | ||
Тип 4 \ (2 (3x — 4) + 1 = 5 \) Другой метод: \ (2 (3x — 4) + 1 = 5 \) Упражнение для самостоятельной маркировки | ||
Тип 5 \ (\ frac {2x + 3} {5} + 7 = \ frac {3x + 12} {3} \) Упражнение для самостоятельной маркировки | ||
Ссылка на учебную программу | ||
Генератор домашних заданий по математике | 101 Вычислительная техника
В этой задаче мы создали клиентский скрипт с использованием HTML, CSS и JavaScript, чтобы помочь учителю математики создавать домашние задания для своего класса.
На нашей HTML-странице используется веб-форма, в которой учитель может выбирать различные варианты в зависимости от навыков математики, которые он хочет изучить, и желаемого уровня сложности.
Код JavaScript, прикрепленный к кнопке «Создать рабочий лист» , извлекает данные, введенные пользователем, из различных раскрывающихся списков. Затем он использует их для создания списка арифметических уравнений и отображения их на странице HTML.
Код HTML, CSS и JavaScript
См. Генератор домашних заданий Pen Maths от 101 Computing (@ 101Computing) на CodePen.
Ваша задача
Выполните обратную разработку этого кода JavaScript, чтобы понять, как он работает. Например, вы можете определить:
- Назначение функции getDropDownListValue () , определенной в строках с 1 по 4 ?
- Назначение строк с 7 по 49 ?
- Назначение корпуса переключателя на строках с 12 по 33 ?
- Назначение цикла для цикла на строке 37 ?
- Назначение строк 38, 39 и 40 ?
- Назначение строки 42 ?
- Назначение строки 44 ?
Проблема №1: 2 или 3 операнда на уравнение?
Теперь, когда вы понимаете, как работает этот код, дополните его, чтобы учитель математики мог выбрать количество операндов для каждого уравнения.
 Например, если учитель математики выберет два операнда, он сгенерирует уравнения, такие как «2 + 7». Если учитель выбирает три операнда, примером уравнения может быть «2 + 4-7».
Например, если учитель математики выберет два операнда, он сгенерирует уравнения, такие как «2 + 7». Если учитель выбирает три операнда, примером уравнения может быть «2 + 4-7».Задача № 2: найти недостающий операнд
Измените код, чтобы сгенерировать уравнения с отсутствующим операндом. Например: «2 + ??? = 9 ”
Задача № 3: Линейные уравнения
Измените код, чтобы сгенерировать линейные уравнения. Например: «3x + 2 = 11».
Задача № 4: квадратные уравнения
Измените код, чтобы генерировать квадратные уравнения.Например: «4x 2 + 5x + 2 = 0 ″.
3.1: Генерация множеств — математика LibreTexts
Теперь мы увидели несколько различных типов групп: группы симметрий геометрического объекта, целые числа при сложении, целые числа по модулю \ (n \) и перестановки. Мы можем легко визуализировать объекты, связанные с группой, такие как геометрический объект, числа или обозначение кос для перестановок, но как мы можем визуализировать саму группу?
Отличный способ сделать это — определить набор генераторов для группы. В группе мы всегда можем объединить некоторые элементы, используя групповую операцию, чтобы получить другой групповой элемент. Генераторы — это некоторые особые элементы, которые мы выбираем, которые можно использовать для доступа к любому другому элементу в группе.
В группе мы всегда можем объединить некоторые элементы, используя групповую операцию, чтобы получить другой групповой элемент. Генераторы — это некоторые особые элементы, которые мы выбираем, которые можно использовать для доступа к любому другому элементу в группе.
В качестве примера вспомните группу диэдра, симметрии \ (n \) -стороннего многоугольника. У всех есть симметрии \ (2n \), но мы можем построить любую из симметрий, используя лишь небольшой поворот и переворот. Для симметрии равностороннего треугольника мы обозначим \ (\ rho \) поворот на \ (120 \) градусов, а \ (f \) — переворот по одной из осей треугольника.2 \). Таким образом, \ (\ {f, \ rho \} \) — это набор образующих для группы диэдра.
Вот формальное определение:
Определение 3.0.0:
Пусть \ (G \) — группа, а \ (S \) — подмножество \ (G \). Мы говорим, что \ (S \) порождает \ (G \) (и что \ (S \) — это набор из порождающих для \ (G \)), если каждый элемент \ (G \) может быть выражен как произведение элементов из \ (S \) и их обратных.
Мы включаем в определение инверсии образующих, потому что знаем, что у каждого элемента есть инверсия.{-1} = e \).)
С другой стороны, для любой группы \ (G \) мы определенно можем взять саму \ (G \) в качестве порождающего множества! Тогда каждый элемент считается «генератором», поэтому каждый элемент может быть записан как (тривиальное) произведение генераторов. Это говорит нам о том, что для любой группы мы можем найти генераторную установку. Обычно мы стараемся найти генераторную установку как можно меньше. Иногда, однако, может быть интересна генераторная установка большего размера, если она помогает нам лучше понять группу, о которой идет речь.
Когда у нас есть порождающий набор для графа \ (G \), мы можем создать очень красивую визуализацию группы, называемой графом Кэли.Под графом мы понимаем количество точек (называемых вершинами), соединенных некоторыми стрелками (называемыми ребрами). Графики хороши для отслеживания взаимосвязей между вещами и появляются во многих-многих местах математики и приложений.
Граф Кэли группы имеет по одной вершине для каждого элемента \ (x \) в группе. Из каждой вершины выходит одна стрелка для каждого генератора \ (g \), указывающая на элемент \ (gx \). (Это создает левый граф Кэли. На правом графике Кэли есть стрелки, указывающие от \ (x \) к \ (xg \).) Обычно мы делаем стрелки разного цвета, чтобы соответствовать разным генераторам; это очень полезно для визуализации структуры группы!
Для группы диэдра мы нашли набор образующих с двумя элементами: вращение и переворот по одной из осей. На самом деле группа диэдра имеет много разных наборов образующих размера два! Например, мы могли бы выбрать вращение по часовой стрелке вместо вращения против часовой стрелки. Или мы могли выбрать любой другой флип.Но получившийся граф Кэли был бы более или менее таким же.
Рисунок 3.1: Граф Кэли группы диэдра, созданный переворотом и вращением.
Совершенно другой набор образующих для двугранной группы состоит в том, чтобы сделать два разных переворота по осям, которые примыкают друг к другу. Назовем их \ (f_1 \) и \ (f_2 \). Фактически вы все еще можете записать любой элемент диэдральной группы как произведение этих двух флипов. И полученный график Кэли выглядит совсем иначе.2 = 1 \). Рисовать стрелки в обоих направлениях от каждого элемента утомительно, поэтому в этом случае мы иногда опускаем стрелки.
Назовем их \ (f_1 \) и \ (f_2 \). Фактически вы все еще можете записать любой элемент диэдральной группы как произведение этих двух флипов. И полученный график Кэли выглядит совсем иначе.2 = 1 \). Рисовать стрелки в обоих направлениях от каждого элемента утомительно, поэтому в этом случае мы иногда опускаем стрелки.
Упражнение 3.0.1
Определите образующие для группы перестановок \ (S_3 \). Постройте граф Кэли.
- Том Дентон (Институт Филдса / Йоркский университет в Торонто)
Генератор задач геометрии | Мэти МакМэтерсон
Обновление 1/22 : В конец сообщения добавлена еще одна ссылка на Генератор проблем.Исходный пост находится ниже:
Краткая версия этого сообщения: посмотрите это видео, в котором я использую Geogebra и Javascript, чтобы облегчить себе жизнь
Полная версия сообщения:
Итак, вот что меня раздражает как учителя геометрии: создавать свои собственные задачи по геометрии, включающие решение задачи алгебры, — заноза для меня. Некоторые примеры:
Некоторые примеры:
Сложность создания этих проблем:
- Любое алгебраическое выражение, которое вы создаете, обычно должно включать положительные переменные или положительный результат оценки (поскольку это не имеет смысла для x = 7, но когда вы его вставляете, длина AB = -4)
- Выражения алгебры зависят друг от друга (например: если у вас есть две параллельные прямые и один из углов равен 47, то любая задача алгебры, которую необходимо решить учащимся, должна в конечном итоге оказаться равной 47)
- В учебниках обычно не хватает таких задач, чтобы они стоили вашего времени, но они действительно полезны для закрепления навыков алгебры при обучении геометрии.
Прямо сейчас я провожу курс интервенции для второкурсников, изучающих геометрию, так что мне бы понравился , если бы я мог найти массу этих задач, потому что они позволяют мне говорить о геометрии и алгебре одновременно (что отлично!)
К счастью для меня, я создал программу Geogebra, которая позволяет мне генерировать столько изображений, сколько я хочу. Он использует Javascript для случайного создания проблем и вывода их на экран, затем я использую Geogebra, чтобы он выглядел красиво, и сохраняю его как изображение, которое я могу вставить в текстовый документ.Благодаря этому я могу сгенерировать 20 задач за 20 минут — картинки, алгебру и все ответы.
Он использует Javascript для случайного создания проблем и вывода их на экран, затем я использую Geogebra, чтобы он выглядел красиво, и сохраняю его как изображение, которое я могу вставить в текстовый документ.Благодаря этому я могу сгенерировать 20 задач за 20 минут — картинки, алгебру и все ответы.
Итак, если вам интересно, как я это делаю, я снял видео и выложил его на Youtube. Все, что вам нужно, это копия Geogebra и некоторое представление о том, как работает Geogebra. На самом деле вам не нужно знать какое-либо программирование, если вы хотите решать более сложные задачи, вам нужно поиграть с тем, что у меня ниже.
Вот ссылка на видео, где я демонстрирую, как решать свои собственные проблемы
Вот ссылка на код Geogebra Javascript, который вам понадобится
Вот ссылка на более сложную программу, использующую функции, о которых я говорю в видео
Вот ссылка на программу, которая генерирует проблемы подобия
Нравится:
Нравится Загрузка. ..
..
Создание пользовательских рабочих листов предварительной алгебры, алгебры 1, геометрии, алгебры 2, предварительного расчета и исчисления
При ограниченном предложении и, казалось бы, бесконечном спросе на ваше время каждая сэкономленная минута — это еще одна минута, которую вы можете потратить на создание идеального урока, помощь ученику в усвоении сложной концепции или на то, чтобы найти время, чтобы просто вздохнуть. Когда дело доходит до изучения математики, практика помогает достичь совершенства, но чтобы найти правильную практику, нужно время.Вы можете потратить бесчисленные часы на поиски правильных проблем и прийти с пустыми руками. Здесь мы можем помочь. Вам больше не нужно искать в Интернете или в стопке учебников. Всего за несколько минут вы можете создать нужные вопросы с нужными свойствами.
Больше, чем просто модные слова, адаптация к навыкам и стилям обучения учащихся дает сильное чувство ответственности за процесс обучения, которое может иметь долгосрочные последствия. Наши программы позволяют вам делать то, что раньше было невозможно: настраивать домашние задания, викторины и тесты в кратчайшие сроки! Учащиеся и учебная программа могут кардинально меняться из года в год, и ваши оценки должны быть настолько гибкими, насколько это необходимо.
Наши программы позволяют вам делать то, что раньше было невозможно: настраивать домашние задания, викторины и тесты в кратчайшие сроки! Учащиеся и учебная программа могут кардинально меняться из года в год, и ваши оценки должны быть настолько гибкими, насколько это необходимо.
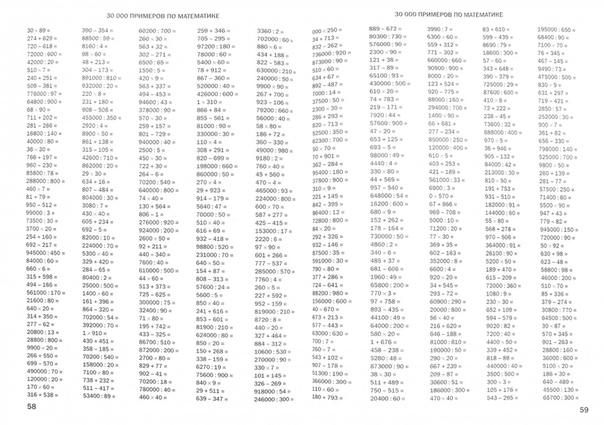
Даже самые полные учебники вынуждены ограничивать количество времени, посвященного какой-либо конкретной теме.Наши программы учитывают ваши варианты и создают желаемые вопросы на вашем компьютере, а не выбирают проблемы из заранее написанного набора. Это позволяет им создавать как можно больше вопросов в мгновение ока. Теперь вы можете закончить тему, когда ваши ученики усвоили ее, а не когда у вас закончатся задачи. Создание собственных заданий означает, что вы точно знаете сложность каждой задачи до того, как она будет напечатана, и вы можете адаптировать свои задания для каждого урока или учащегося, вместо того, чтобы собирать уроки по заранее установленным оценкам.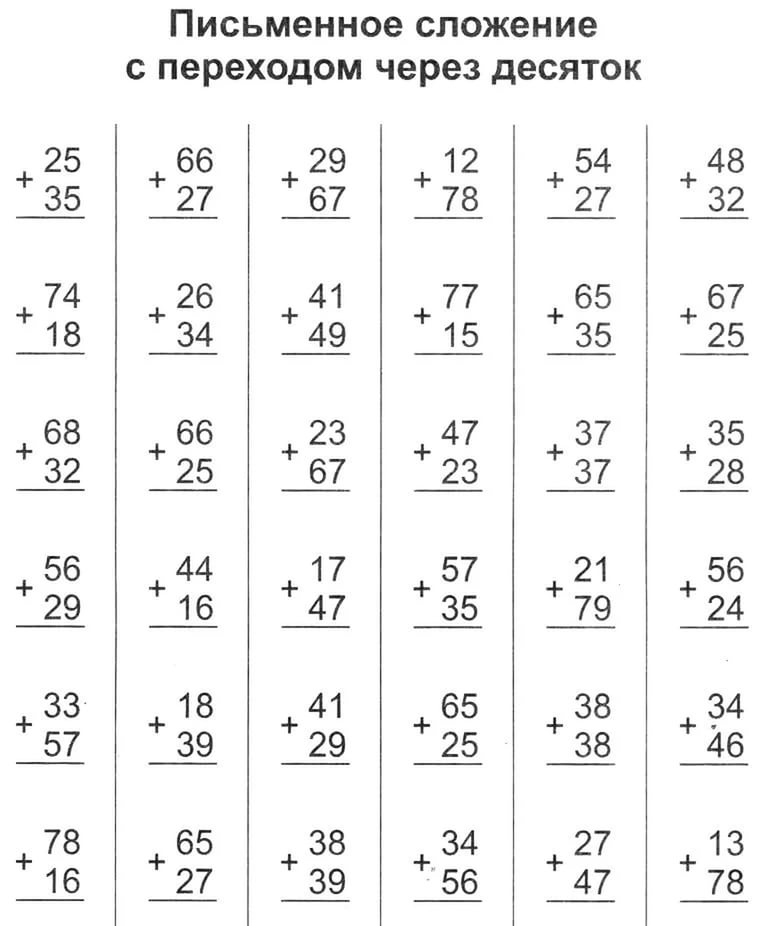


 {" + b + "} i*" + c
{" + b + "} i*" + c
 append(i)
elif fn == "NT":
ends.append(i)
if exp[-1] in NUM:
ends.append(len(exp) - 1)
if exp[0] in NUM:
begins = [-1] + begins
return [(x + 1, y + 1) for x, y in zip(begins, ends)]
def __init__(self):
self.funcs = []
def add_expander(self, func):
self.funcs.append(func)
def complexify(self, num):
return random.choice(self.funcs)(num)
def __rxp__(self, exp):
x, y = random.choice(self.extract_nums(exp))
exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:]
return exp
def randexpr(self, ans, steps):
e = str(ans)
for i in range(steps):
e = self.__rxp__(e)
return e
def unmin(*args, acc=2):
r = []
for arg in args:
f = round(arg, acc)
if f > 0:
f = str(f)
else:
f = "(" + str(f) + ")"
r.append(f)
return r
def __c_sum(num):
a = round(random.
append(i)
elif fn == "NT":
ends.append(i)
if exp[-1] in NUM:
ends.append(len(exp) - 1)
if exp[0] in NUM:
begins = [-1] + begins
return [(x + 1, y + 1) for x, y in zip(begins, ends)]
def __init__(self):
self.funcs = []
def add_expander(self, func):
self.funcs.append(func)
def complexify(self, num):
return random.choice(self.funcs)(num)
def __rxp__(self, exp):
x, y = random.choice(self.extract_nums(exp))
exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:]
return exp
def randexpr(self, ans, steps):
e = str(ans)
for i in range(steps):
e = self.__rxp__(e)
return e
def unmin(*args, acc=2):
r = []
for arg in args:
f = round(arg, acc)
if f > 0:
f = str(f)
else:
f = "(" + str(f) + ")"
r.append(f)
return r
def __c_sum(num):
a = round(random. {" + b + "} i*" + c
gen = ProblemGenerator()
gen.add_expander(__l_sum)
gen.add_expander(__l_div)
gen.add_expander(__l_pow)
gen.add_expander(__l_sqrt)
gen.add_expander(__l_int)
gen.add_expander(__l_sig)
import matplotlib.pyplot as plt
plt.axis("off")
latex_expression = gen.randexpr(1, 30) # 30 раз заменяем. Выражение будет равно 1
plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=15)
plt.show()
{" + b + "} i*" + c
gen = ProblemGenerator()
gen.add_expander(__l_sum)
gen.add_expander(__l_div)
gen.add_expander(__l_pow)
gen.add_expander(__l_sqrt)
gen.add_expander(__l_int)
gen.add_expander(__l_sig)
import matplotlib.pyplot as plt
plt.axis("off")
latex_expression = gen.randexpr(1, 30) # 30 раз заменяем. Выражение будет равно 1
plt.text(0.5, 0.5, "$" + latex_expression + "$", horizontalalignment='center', verticalalignment='center', fontsize=15)
plt.show()

 Невозможно предсказать, насколько быстро вы разовьете уверенность в решении уравнений определенного типа, но обычно примеры будут немного усложняться каждый раз, когда вы нажимаете кнопку «Далее». Кнопка перезапуска предоставляется, если сгенерированные вопросы начинают становиться слишком сложными. Эта кнопка перезапускает уровень сложности, но отображает другие уравнения.
Невозможно предсказать, насколько быстро вы разовьете уверенность в решении уравнений определенного типа, но обычно примеры будут немного усложняться каждый раз, когда вы нажимаете кнопку «Далее». Кнопка перезапуска предоставляется, если сгенерированные вопросы начинают становиться слишком сложными. Эта кнопка перезапускает уровень сложности, но отображает другие уравнения.