Цифра 0 задания для дошкольников. Учим цифры с ребенком

Учится считать малыш с малых лет. Уже в год умная мама, подавая ребенку игрушку, проговаривает: «Один мячик», «Два шарика»… Ребенок все это запоминает и, как правило, умеет считать до десяти уже годам к пяти точно. Но совершенно другое дело — цифры. Малыш пока не ассоциирует количество предметов с их изображением, и этому ребенка нужно учить. Не стоит вбивать в голову цифры раньше пяти лет, а вот с пяти-шести уже можно, а в семь перед самой школой — даже нужно.

Если этап обучения счету пропущен, то есть ребенок считать еще не умеет, несмотря на старший дошкольный возраст, придется учиться считать и учить цифры одновременно. Начать интереснее всего со стихов про цифры. Отличное, запоминающееся стихотворение есть у С. Маршака: Весёлый счёт (прочитать стихотворение >>)

Наибольшую результативность в обучении деток показывают комплексные задания. На одном листе собраны задания, касающиеся изучаемой цифры и ее предшественников (то есть повторение изученного).

Один лист идет на два занятия. Первое — непосредственно изучение цифры. Ребенок смотрит, как она выглядит, раскрашивает, ассоциирует с количеством предметов на картинке. 20 минут на одно занятие вполне хватит. После того, как цифру выучили, рекомендуем распечатать и расположить на видном месте в комнате соответствующую карточку с цифрой.

Второе занятие — закрепление изученного. Ребенок узнает состав числа, выполняет простейшие манипуляции с числами.

Скачать и распечатать задания «Учим цифры с ребенком»

Чтобы скачать лист, для начала кликните на него левой кнопкой мыши и откройте в полном размере. Далее клик правой кнопкой мыши, выбираем «Сохранить картинку как…» и сохраняем себе на компьютер, а с него распечатываем.

Итак, лист распечатали. Текст заданий читает родитель или преподаватель. Самое первое задание при знакомстве с цифрой — заштриховать ее. Не раскрасить, а именно заштриховать. Такое задание, как штриховка, отлично готовит руку к письму, ребенок учится владеть своими пальчиками, это позитивно отразится и на почерке.

Затем из цепочки цифр выбираем ту, которую изучили, проговариваем, раскрашиваем.

Следующее задание — раскраска. Раскрашиваем одинаково помеченные области одним цветом.

МКОУ «Ниж – Суетская средняя

общеобразовательная школа

имени Анатолия Карпенко»

Открытый урок

математики в 1 классе

по теме «Число 0»

Провела: Ильиных Т. И.

с. Нижняя Суетка

Тема: «Число и цифра 0»

Цель: введение числа 0 как характеристика пустого множества и начало отсчёта на числовом отрезке.

Задачи:
1) образовательные:
— создать условия для формирования представлений учащихся о числе ноль, характеристике пустого множества и начала отсчёта на числовом отрезке, познакомить с соответствующей цифрой и формировать умение писать цифру ноль; для закрепления умения учащихся — устанавливать отношения между числами, для развития умения — писать изученные цифры;

2) развивающие:
— развивать наблюдательность, внимание, математическую речь, мыслительные операции у учащихся;
3) воспитательные:
— способствовать воспитанию дружеских взаимоотношений, взаимопонимания, умения работать друг с другом; воспитанию интереса к предмету, адекватно оценивать результат своей работы;
здоровьесберегающие:
— сохранять здоровье детей путём чередования различных видов деятельности и активного отдыха, использования ИКТ, создания комфортной и доверительной атмосферы в классе.
УУД:
познавательные УУД: создание и нахождение путей выхода из проблемной ситуации; выполнение действий по заданному алгоритму, выполнение заданий с использованием материального объекта.
коммуникативные УУД: сотрудничество учеников в паре, планирование совместной деятельности.
регулятивные УУД: контролирование своей деятельности по ходу и через результат выполнения задания, определение последовательности действий.
личностные УУД: проявление познавательной инициативы в оказании помощи соученикам.

Ход урока:

1.Самоопределение к учебной деятельности

Цель этапа: Организовать направленное внимание на начало урока.

Вот звонок нам дал сигнал:
Поработать час настал.

Так что время не теряем и работать начинаем!

И прекрасна, и сильна

Математика – страна.

— Скажите, ребята, с какой целью вы пришли сегодня на урок?
/ Учиться думать, решать, рассуждать/

2. Актуализация опорных знаний

Цель этапа: Дальнейшее успешное усвоение новых знаний или учебных действий

Чему учились на прошлом уроке?

/увеличивать и уменьшать числа на несколько единиц/

С чего начнем урок?

А начнем мы наш урок с математической разминки.

Работа в паре /друг другу помогаем/

1. Игра «По местам» — Поставь цифры в порядке возрастания, убывания.

10 5 7 4 3 9 8 6 2 1 (поставить карточки на доске)

Проверка и оценка

Работает каждый сам

Выходят к доске по одному, если ошибка показывают с места правильный ответ.

2. Решение примеров. Игра »Паровозик».

Каждый вагончик везет примеры для вас. Читаем примеры по-разному громко, ответ – веером или числом

3.Постановка цели урока. Открытие нового.

Цель этапа: Сформировать представления детей о том, что нового они узнают на уроке, чему научатся .

Создание проблемной ситуации.

Ответьте, сколько цветочков у меня в руке? (3) Убираю по одному. А сейчас? (нисколько 0)

Сколько дедушек у нас в классе? (нисколько)

Сколько яблок может вырасти на сливе? (ни одного).

Сколько говорящих собак вы знаете?

Так как можно обозначить “ни сколько”, “ни одного”?

Какой цифрой обозначим?

Определение темы урока.

Назовите тему урока. (Число ноль)

Положите 3 треугольника. Рядом поставьте соответствующее число.

Уменьшите количество треугольников на 1. Сколько треугольников осталось?

Где место числа 2 в числовом ряду? (перед числом 3) Поставьте число 2.

Уменьши количество треугольников на 1. Сколько треугольников осталось? 1

Где место числа 1 в числовом ряду? Перед числом 2 поставь число 1(1 2 3)

Уменьши количество треугольников на 1. Сколько треугольников осталось?

Чему будем учиться на уроке? (, познакомимся с числом и цифрой 0, научимся писать цифру 0

Число 0 показываю

На что похожа цифра 0?

Цифра вроде буквы О – это ноль иль ничего.

Круглый ноль такой хорошенький,

Но не значит ничегошеньки.

Как получили ноль? 1-1 (на доске пример 1-1=0)

Покажите 0 кругов, 0 кругов.

Ноль появился в Индии, обозначался кружком, называли его «сифр». Спустя несколько веков ему дали название «нуль», что означает «ничто».

Ноль единственная цифра, которой поставлен памятник в Венгрии, в центре города Будапешт. От этого памятника отмеряются все расстояния в стране.(слайд)

4.Первичное восприятие и усвоение нового теоретического учебного материала.

Цель этапа: Привлечение внимания детей к принципиально новым сведениям, развитие умения распознавать цифру 0.

Где в жизни мы встречаемся с числом 0?

Ноль – важная цифра в нашей счетной системе. Он ничего не значит, но если встанет справа от числа, то число увеличится в 10 раз. (показать рисунок)

Кто сможет назвать числа, в которых используют ноль? (10,100,500,2000)

А если ноль поставим слева от числа (показать рисунок),то получим странные числа.

Вам они встречались?

(01- пожарная служба, 02 – полиция, 03- скорая помощь, 04 – газовая служба)

Где место ноля на числовом отрезке?

Слайд
В народе говорят « Начнем с нуля».
-Когда так говорят?

Физ.минутка. («Солнце глянуло в кроватку….»)

Цель этапа: Смена вида деятельности

Какую задачу урока сейчас поставим?

5.Первичное закрепление. Работа в тетрадях.

Цель этапа : Сформировать навыки написания цифры 0.

— Сейчас мы будем учиться писать цифру 0.

ОТКРОЙТЕ ТЕТРАДИ. Положите с наклоном, сядьте прямо.

Сколько элементов у цифры 0? (1 овал)

Начинаем писать чуть ниже вершины верхнего правого угла, закругляем, касаясь верхней стороны клетки, ведем вниз, закругляем, касаясь середины нижней стороны клетки, закругляем и ведем вверх к началу овала.

Напишите цифру в тетради. Выберите самую красивую, правильно написанную цифру, поставьте точку под ней.

Справились с этой работой?

6.Обобщение усвоенного.

Цель этапа: Закрепить, повторить, продолжить формирование УУД.

Работа с учебником. Стр.70

Прочитайте, на какой вопрос мы должны ответить.

Ответили?(Да.)

Итак, сейчас очень важно выполнить какую работу?

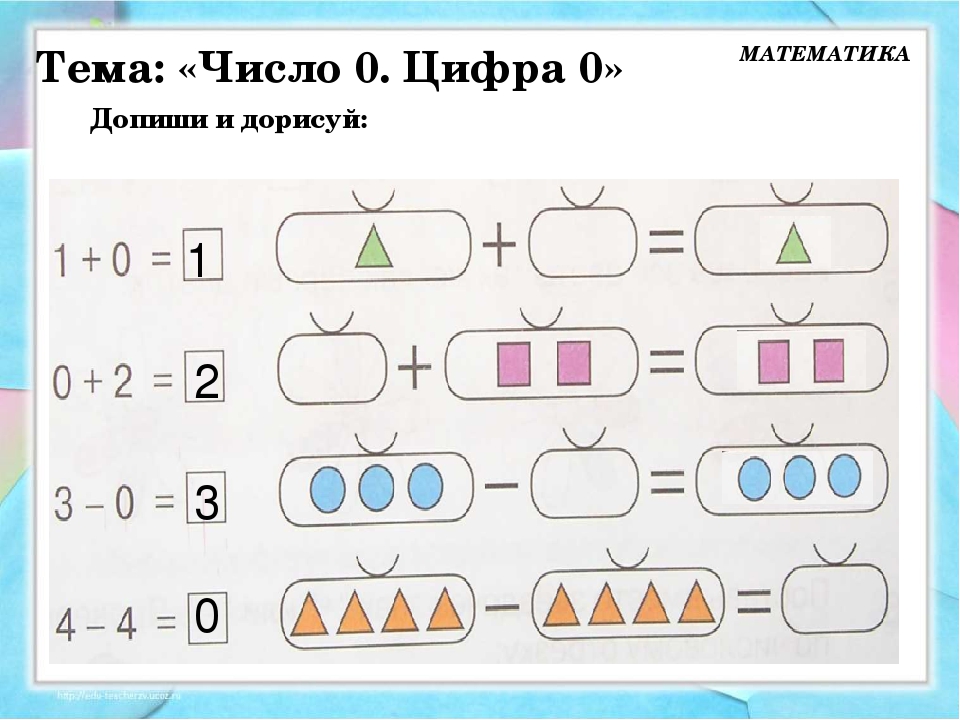
Закрепить полученные знания. С помощью рисунков объяснить, как получить ноль?

Рассмотрите картинки ниже.

Что изображено? Прочитайте вопрос. Что такое равенство?

Работа в группе

Составьте рассказы по равенствам, опираясь на рисунок. 1 минута

Заслушивание ответов

Какое равенство подходит к картинке?

Рассмотрите следующий рисунок. Что было, что изменилось? (Было 3 листочка, 1 улетел) Сколько осталось?

Как записать? Стало листочков больше или меньше?

Сравните 2 и 3. и т.д.

Индивидуальная работа

Составить по рисунку рассказ и выполнить запись.

1 работает у доски. Проверка. Оценка

7.Подведение итогов

Какие задача мы ставили в начале урока?

Мы их выполнили?

Что означает число 0?

В математике эта цифра нужна?

Чего у нас в классе 0?

8. Рефлексия

Покажите ваши цветочки. У кого больше желтого? Зеленого?

А на «дереве успеха» покажите на какую веточку вы сегодня взобрались.

Учитель: Я вижу, что многие добрались до самой высокой веточки, а это значит, что урок состоялся не зря. И каждый из вас ещё больше полюбил самую точную науку математику.

За активную работу на уроке я хочу наградить ребят …

Конспект занятия по математике

Знакомство с 0.

Цель: Познакомить с числом и цифрой 0.

Задачи.

Образовательные: Образование числа 0, его место в числовом ряду.

Развивающие: Развитие логики мышления, математической смекалки.

Воспитательные: Прививать любовь к математике.

Оборудование: плоскостные персонажи сказки «Колобок»; цифра 0. Раздаточный материал: на столах у детей крупные семена тыквы, фасоль, цветные палочки.

Ход занятия.

Дидактическая игра «Что изменилось?»

Цель игры: развивать произвольное внимание и кратковременную память; воспитывать честность.

Материал: несколько небольших игрушек или других предметов, знакомых детям.

Ход игры: на стол ставится несколько небольших игрушек или других предметов, хорошо знакомых детям. Выбирается ведущий, который предлагает играющим запомнить, что и в каком порядке стоит на столе. Затем ведущий предлагается участникам отвернуться, а сам в это время меняет местами несколько игрушек и предлагает ребятам отгадать, что изменилось на столе. За каждый правильный ответ ведущий вручает фишку. Выигрывает тот, кто соберёт больше всех фишек.

– Ребята, скажите, что такое сказка? (Это когда, что-то волшебное).

— А вам хотелось бы попасть в математическую сказку? Тогда давайте отправимся в путешествие.

Ребята, ну-ка возьмите в руки бинокль (руками изобразить бинокль), что же вы видите? (На доске появляется изображение колобка). (Колобок убежал от бабушки).

Давайте вспомним начало сказки. (Дети вместе с воспитателем вспоминают).

— … Катится, катится Колобок, а навстречу ему Заяц (на доске появляется изображение зайца).

Колобок, Колобок я тебя съем!

Не ешь меня Зайка, лучше дай мне задачи решить.

Давайте поможем Колобку решить трудные задачи, иначе Заяц его съест! (Дети решают задачи: карточка из картотеки «Праздник числа», «Думай, считай, отгадывай!» Задачи на сообразительность -0-:

Стоит в поле дуб. На дубе 3 ветки. На каждой ветке по 3 яблока. Сколько всего яблок?

(Нисколько).

На груше росло 10 груш, а на иве на 2 меньше. Сколько груш росло на иве?

(Нисколько, так как на иве груши не растут).

Заяц отпустил Колобка.

А, вы, ребята, догадались, с какой цифрой мы сегодня познакомимся?

Правильно, ноль!

Ну почему мы попали именно в эту сказку?

Как вы думаете? (Колобок похож на 0).

На что ещё похожа цифра 0? (карточка «на что похожа цифра?»).

Не ешь меня, Волк, лучше вопросы трудные и задания интересные задавай!

(Карточка. Задачи в стихах -0-). Задача про гусей.

Семь рассерженных гусей,
Семь отчаянных друзей
Ходят-бродят: «Га-га-га!»
Тут хозяйка позвала их: —
Есть хотите? — Да-да-да!
И пошли ватагой всей
Семь рассерженных гусей.
Семь гусей ушли кормиться,
Сколько же осталось птицы?

(Нисколько).

Дети во время задачи выкладывают у себя на столе семена тыквы, фасоль. Покажите ответ, выложите цифру 0 из палочек. Давайте покажем в воздухе как правильно написать цифру 0.

А теперь выведите пальчиком на ладошке друг друга эту цифру, теперь на спинах друг друга.

Вы и Колобок справились с заданием. Волк отпустил колобка.

Колобок, Колобок, я тебя съем!

Не ешь меня, Медведь, лучше задание мне и детям давай. (Карточка. Задачи в стихах -0-… Повезло опять Егорке…, Барсучиха — …)

Повезло опять Егорке,
У реки сидит не зря.
Два карасика в ведерке
И четыре пескаря.
Но смотрите — у ведерка
Появился хитрый кот…
Сколько рыб домой Егорка
На уху нам принесет?

(Нисколько)

Барсучиха-бабушка
Испекла оладушков.
Угостила двух внучат —
Двух драчливых барсучат.
А внучата не наелись,
С ревом блюдцами стучат.
Ну-ка, сколько барсучат
Ждут добавки и молчат?

(Молча не ждет никто, а с ревом ждут двое)

Дети решают задачи.

Отпустил Медведь Колобка.

Катится, катится, Колобок, а на встречу ему Лиса.

Колобок, Колобок, я тебя съем!

Не ешь меня, Лиса, скажи, что ребятам сделать, чтобы ты меня не съела.

Лиса предлагает детям открыть прописи и выполнить задания. Самостоятельная работа детей. Лиса отпускает колобка.

Анализ, итог занятия:

Ребята, если бы Лиса съела Колобка, то, что бы от него осталось? (ничего, ноль).

С какой цифрой мы сегодня познакомились?

На что похожа эта цифра?

Если вам понравилось занятие то покажите большой палец кверху, а если вам было скучно то покажите большой палец к низу.

Тема урока: Число и цифра 0

Цели:

Сформировать представление о числе 0, овладеть умением выявлять свойства нуля с помощью наглядных моделей; писать цифру 0; закреплять навыки счета в пределах 9;

Развивать творческие способности учащихся, внимание, мыслительные операции;

Воспитывать умения анализировать свою деятельность;

Оборудование: набор цифр от 0 до 9, ель, разноуровневые карточки для индивидуальной работы

Ход урока.

Организационный момент.

Мы – умные!

Мы – дружные!

Мы – внимательные!

Мы – старательные!

Мы – отлично учимся!

Всё у нас получится!

Посмотрите на своего соседа по парте и подарите друг другу улыбку, настройтесь на работу. Проверьте посадку.

II . Актуализация знаний.

Сегодня математика приглашает в своё царство всех, кто не боится цифр и вычислений. Мы с вами стараемся познать эту интересную науку, преодолевая трудности, ведь наш девиз: « У меня всё получится».

Работа с числовым рядом (веер цифр)

Назовите число, которое стоит за числом 4 (5)

Назовите число, которое стоит перед числом 7. (6)

Какое число стоит между числами 7 и 9? (8)

Назови соседей числа 3 (2,4)

Найди сумму чисел 4 и 5 (9)

Найди разность чисел 8 и 1(7)

На доске записаны числа (набор цифр):

3 6 1 4 7 9 2 5 8

Какие задания можно предложить?

Расположить числа в порядке увеличения, уменьшения, сравнить, составить равенства и неравенства.

2. Числовые равенства и неравенства.

Наш друг Незнайка постарался за вас и составил равенство. Проверьте, все ли он правильно сделал?

Как помочь Незнайке, ничего не зачеркивая и не исправляя числа?

4=5 (4=5-1) (1+4=5)

3. Состав числа 9.

2+…=9 …+2=9

2=7 9-…= 2

III . Постановка темы урока.

Начинаем мы опять

Решать, отгадывать, смекать!

Росли 2 сосны, на каждой сосне по 2 ветки, на каждой ветке по 2 яблока.

Сколько всего яблок?

Нисколько, на соснах яблоки не растут.

Подумайте, как можно по-другому сказать? (ни одной)

Догадались, какова у нас тема урока?

Число 0. Цифра 0. Это слово пришло к нам из латинского языка. Означает «ничто».

IV . Открытие новых знаний.

1.Введение числа и цифры 0. Соотнесение числа с количеством предметов.

У Маши было 9 конфет. 4 конфеты она дала младшему брату, 4 съела сама и 1 угостила папу. Сколько конфет осталось у Маши?

Что же обозначает число 0? (нет предметов, пустоту, нисколько, ни одной не осталось)

Какой цифрой будем записывать число 0?

Физкультминутка (подвижная)

Буратино потянулся-

Раз нагнулся, два нагнулся,

Руки в стороны развёл-

Видно ключик не нашёл:

Чтобы ключик нам достать-

Нужно на носочки встать.

Буратино выше встал,

Поглядите- ка, достал.

2. Написание цифры по образцу. Работа по учебнику с.31

Цифра 0 состоит из одного элемента – большого овала. Начинаем писать чуть ниже вершины правой стороны клеточки в левую сторону, округляем, касаемся верхней линии клеточки, округляем, вниз, округляем вправо, касаемся нижней линии клеточки, округляем, вверх и соединяем.

– Вспоминаем правила посадки при письме, учитель показывает образец написания нуля.

3. Определение места 0 на числовом отрезке с. 30

Число 0 не знает, где его место. Какое место ему занять на отрезке. Почему вы так думаете?

В народе часто говорят: «Начнем с нуля…», когда так говорят?

(начинают сначала, на пустом месте).

Сравните 0 с другими числами отрезка.

На сколько 0 меньше 1? На сколько 1 больше 0?

4. Свойства нуля:

Цифра вроде буквы 0 –

Это 0 иль ничего.

О его особых свойствах

Мы поведём сейчас рассказ.

Что значит эта запись: а+0=…. (а — любое число, если к любому числу прибавить 0, то получится то же самое число а+0=а) Также устанавливаются другие свойства: 0+а=а, а-0=а, а-а=0

Задание №2.

Итак, ребята, мы познакомились со свойствами 0.

Ещё раз прокомментируйте их

.5. Работа по тетради на печатной основе.

Задание №1

Как его проиллюстрировали? Кто мог цветочки срезать и для кого?

Что получилось в результате?

Физкультминутка (для глаз)

Задание №5.

1 столбик коллективно;

2 столбик — 1ряд;

3 столбик — 2ряд;

4 столбик — 3ряд

V . Первичное закрепление.

Дифференцированная работа.

1.Решение примеров на основе свойств 0.

5-0=5 7-7=0 2+0=2

2. Индивидуальные карточки . Выбираем для себя задание (по сложности) на карточке красный кружок – самое сложное, синий – 2 уровень, зелёный – 1 уровень (простое).

3. Игра «Подумай, где ты встречал 0, в какой службе работает число ноль?»

Пожарная -01, милиция -02, скорая помощь -03

Запишите в тетради эти номера.

VI . Итог урок.

— Что вы узнали на нашем уроке?

Мы познакомились с новым интересным числом. Что вы можете рассказать о нем? (Его нельзя использовать при счете, но без него нельзя обойтись в математике. Оно меньше любого известного нам числа . Мы не можем показать соответствующее ему количество предметов.)

Какие свойства нуля теперь знаете?

Какое задание вам показалось интересным? Сложным?

Расскажите по схеме:

Я запомнил …

Я знаю…

Я смог…

Я научился. …

Как бы вы оценили свою работу? (предлагается три смайлика для оценки)

VII . Дом.задание.

Найти символ числа ноль и выяснить, какую важную роль в математике выполняет ноль. Спасибо за урок.

Мы с вами уже знакомы, пора познакомить своего малыша с цифрами. Цифровой ряд начинается с цифры 0 . Малыша следует сразу знакомить с числом и цифрой 0. Как это сделать? Начните со знакомства с понятием много и ни одного.

В детском саду занятия по математике начинаются с трех лет.

И так, как познакомить малыша с множеством? Как показано на рисунке, спросите у малыша:

Сколько мишек в прямоугольнике слева? (много)

А сколько мишек в прямоугольнике справа? (ни одного)

Поясните малышу, что когда нет ни одного, обозначают цифрой 0 . И покажите малышу цифру ноль. Спросите, на что похожа цифра?

Для закрепления цифры вы можете использовать дидактический материал по математике – это и художественное слово, и ребусы, и веселые задачки, и загадки.

Дидактический материал по математике. Цифра «0

Веселые стихи

Повернуть ее ты можешь,Головой поставить вниз,Цифра будет все такой же, Правда, ведь, скажи? Цифра вроде буквы «О» – Это ноль иль нечего. Круглый ноль такой хорошенький, Но не значит ничегошеньки. С. Маршак Ноль – как обруч. Захочу – По дороге покачу. Где здесь верх и где здесь низ? Бублик в воздухе повис. Если ноль – пустое место, Значит, бублик не из теста.

В этой цифре нет угла –Оттого она кругла.До того она кругла – Покатиться бы могла. Не похож он на пятак, Не похож на бублик, Круглый он, да не дурак, С дыркой, да не бублик! З. Александрова Можем говорить мы смело – У ноля большое дело: Только к цифрам он подходит, Сразу чудо происходит. Ноль встает за единицей – Число десять на странице!

Веселые задачки

На ветке сидит 4 воробья. Подкрался кот, схватил одного. Отгадай, сколько воробьев осталось на ветке?

(Нисколько, все улетели.)

На дубе три ветки, на каждой ветке по 2 груши. Отгадай, сколько всего груш на дубе? (Нисколько.)

Ребус

О т в е т: на-тя-нули.

загадки

Древнерусские афоризмы

• · Ученье имеет корень горький, а плод сладкий.
• · Лучше ногами споткнуться, чем языком.
• · Ум – большое богатство для человека.
• · Меч ранит тело, а злое слово – ум.
• · Давай телу лишь столько, сколько оно требует, а не сколько захочет.

Рекомендуем также

Занятие по математике «Число и цифра 0. Вычитание равных чисел» (подготовительная группа)

Занятие по математике в подготовительной группе

Тема: Число и цифра 0. Вычитание равных чисел.

Цель:

• познакомить с числом 0;

• показать, что при вычитании из числа его самого, получается 0;

• что при сложении и вычитании числа с 0 получается само число;

• отрабатывать навыки счёта в пределах 10;

• проверить умение решать примеры на сложение и вычитание в пределах 10;

• закреплять знание детьми состава изученных чисел.

Ход занятия

1. Организационный момент.

– Посмотрите, сколько к нам пришло гостей. Они хотят посмотреть, чему вы научились. Так давайте, покажем, что мы уже умеем.

— Речевое правило:

Воспитатель: Царица наук – Математика приглашает вас в путешествие.

– Дети, вы любите путешествовать?

– А кто знает, зачем люди путешествуют?

– Вот и мы будем узнавать сегодня что-то новое. А поможет нам в этом кто…?

Узнаете когда отгадаете загадку.

Красный нос, в руках метелка.
Проживает рядом с елкой.
К холодам давно привык
Наш веселый…

– Снеговик поведет нас в математическую страну. Там мы познакомимся с числом и цифрой 0, проверим как вы умеете решать примеры на сложение и вычитание в пределах 10. Побываем в парке повторений, на поляне устного счета, в развлекательном

центре, на улице примерчик, площади задачной и конечно же не забудем веселый перерывчик.

ПАРК ПОВТОРЕНИЙ

– Сколько дней в неделе?

– Какой день недели сегодня?

– Какое сегодня число?

– Какое сейчас время года?

– Какой месяц зимы сейчас идет?

– Сколько месяцев в году?

– С какого месяца начинается год?

Следующая остановка «Поляна устного счета»

2. Актуализация знаний

– Счёт от 0 до 10 в прямом и обратном порядке

– Счет от 3 до 8; от 7 до 10; от 9 до 6; от 7 до 2; (индив.)

– Назови соседей чисел: 3, 6, 8:

– Состав чисел: 8; 9; 10;

Игра «Угадай – ка»

Есть такой Дед-Цифроед,

          Ест он цифры на обед

          Как печенье их таскает.

Вставь каких здесь не хватает:

1,…,3, 4… ,…,7,…,…,10.

Физминутка

– Сегодня на занятии мы познакомимся с числом и цифрой 0. Ребята посмотрите …

Паровозик любопытный

Мимо детского сада проезжал,

На минутку задержался –

И вагоны растерял.

— Давайте поможем ему собрать их на своё место. Только вагончики должны стоять каждый на своём месте, по порядку, как числа.

Когда паровозик соберётся, на доске останутся 2 перевёрнутых вагончика. Создаётся проблемная ситуация.

— А зачем эти вагончики, ведь все цифры от 1 до 9 мы уже собрали? (Выслушиваются предположения детей.)

– Действительно, на этих вагонах такие примеры: 1–1, 10+0.

– Давайте определим место, и ещё раз назовём над чем мы с

вами будем работать на занятии?

Цифра вроде буквы О –

Это ноль иль ничего.

Круглый ноль такой хорошенький,

Но не значит ничегошеньки.

Повернуть её ты можешь,

Головой поставить вниз,

Цифра будет всё такой же,

Правда ведь, скажи?

Беседа: (немного истории).

– Вот посмотрите на него – 0. (показываю карточку с цифрой 0). Его называют нулём или нолём, и обозначают им «ничто». Прибавьте нуль к пяти, получится пять; отнимите нуль от шести, и снова получится шесть. Подумаете, вовсе пустяковая цифра, без которой легко обойтись. Но это вовсе не так. Если разобраться, то выйдет, что нуль – очень даже важная персона. Как написать 10?100? если его нет? Вот так долгое время люди и мучились. Чтобы цифры получались правильными, чтобы вышло именно 102, 1001, а не 12 и 11, приходилось их записывать на особо разграфлённой доске – абаке. Там были клеточки отдельно для единиц, десятков, сотен и т.д. На каждую графу абака клали кружок с нужной цифрой, а место нуля оставляли пустым. Потом это пустое место стали накрывать пустым кружком. Так родился наш нуль. В память об абаке он так и остался похожим на кружок, только немного стал вытянут, как овал. На языке арабов слово “нуль” называется “сифр”. Напоминает вам что-либо? (Сифр-цифра). Так уж получилось, что с тех пор всех его братьев и сестёр стали называть цифрами.

Следующая остановка «Площадь задачная»

Как под ёлкой встали в круг
Зайка, белка и барсук,

Встали ёжик и енот,

Лось, кабан, лиса и кот.
А последним встал медведь,
Сколько всех зверей? Ответь!

7. Итог занятия:

— Ребята вам понравился занятие?

— С какой новой цифрой и числом познакомились?

— Какое задание понравилось больше всего?

Следующая остановка «Веселый перерывчик»

– У вас на столах дощечки, пластилин. После перерыва будем лепить с вами цифры. Каждый вытянет карточку с цифрой и попытается вылепить её из пластилина. После того, как дети вылепят цифры, можно сделать выставку работ. А самое главное можно в игровой форме порешать с этими карточками примеры.

Конспект занятия по ФЭМП в старшей группе «Число и цифра 0», «Число и цифра 10»

Конспект занятия по ФЭМП в старшей группе

Образовательная область: «Познание»

Раздел: ФЭМП

Тема: «Число и цифра 0». «Число и цифра 10».
Программное содержание: Познакомить детей с числом 10 и цифрой 0.
Показать образование числа 10; учить порядковому счету в пределах 10, отсчитывать предметы и соотносить их с числом. Уточнять знания о последовательности чисел в числовом ряду, о соседях числа. Вызвать интерес к получаемым знаниям.

Материал:
Демонстрационный материал:
1. Цифры от 0 до 10 в наборном полотне;
2. 10 пирожков для наборного полотна;
3. Схема к стихотворению В. Орлова «Я считаю»
4. Рисунок с изображением девочки.
Раздаточный материал:
1. Листы бумаги;
2. Счетные палочки;
З. Карандаши.

Ход занятия.

I. Аутотренинг.
Мы маленькие огоньки.
Мы любим маму и папу.
Любим прыгать и играть.
А еще мы любим наш детский сад,
Потому, что он дает нам знания.
Вот и сегодня на математике
Мы узнаем много нового и интересного.

Пальчиковая гимнастика.
Предлагаю вспомнить сколько пальчиков на руке, посчитать и загнуть каждый пальчик (счет на русском, затем на казахском языке).

Затем соединить указательный и большой пальцы кружочком и почувствовать ветерок другой рукой.
— Почему вы почувствовали ветерок?
(Потому что кружок пустой)

Нарисуйте кружок на листе бумаги.
«Рисовали просто круг

Получилась цифра вдруг.
Эту цифру назовем
Круглым толстеньким нулем».

Показываю цифру ноль.
Вот эта цифра ноль, она такая кругленькая, как баранка или колесо, а еще похожа на букву О.
«Круглый ноль такой хорошенький, но не значит ничегошеньки».

Угадайте загадку.
«На столе лежали груши,
Кто- то эти груши скушал.
Отвечай скорей изволь.
Сколько груш осталось?» (Ноль)
Ноль — это ничего, пусто.
Эта цифра самая маленькая, потому что ничего не значит. И место ее в числовом ряде перед 1.

Ставлю цифру 0 перед единицей в наборное полотно.

— Цифра 0 обозначает число 0, запомните место этого числа в числовом ряду.

— Какую новую цифру мы сейчас узнали?
— Цифру 0.
— Перед какой цифрой в числовом ряду стоит цифра 0. (перед единицей)

II.
Впереди нас ждет сказка. Сядьте удобно, где ваши глазки, готовы ли они смотреть, где ваши ушки, они готовы слушать.
— Я вам расскажу сказку про цифру.
— Однажды цифры поспорили с нулем и стали его дразнить:
— Ты, хоть, тоже цифра, но ровнехонько ничего не значишь! Вот мальчик возьмет цифру два и поставит два кубика, а возьмет тебя и ничего не поставит.
— Правда, правда, ничего — сказала единица.
— Ничевочка, ничевочка — затараторили цифры.
— Глупые вы, ничего не понимаете — сказал ноль.
— Вот ты единица значишь только один предмет, а я встану рядом с тобой справа и предметов станет ни один, а сразу десять.
— Теперь ты уже не 1, а совсем другая цифра 10.

Вот она — цифра десять. Значит цифра состоит из двух чисел 1 и 0.

С тех пор единица подружилась с нулем. И все остальные цифры поняли, что если ноль встанет с ними рядом, он сделает их на много больше.
— Как вы думаете, после какой цифры в числовом ряду встанет число 10.
— (После цифры 9,)
— Почему?
— (Потому что 10 больше 9).
— С тех пор все цифры стали жить дружно.
— Ноль был очень занятой, он много думал и писал. Поэтому редко появлялся со всеми цифрами. (убрать цифру ноль,)

III.
Услышав эту историю девочка Мадина (рисунок с изображением девочки,) и решила устроить праздник в честь примирения цифр.
«Спечь задумала Мадина
Пирожков из пластилина
десять цифр пригласить,
Пирожками угостить.
Вышло девять пирожков.
Стол накрыт и чай готов”

Работа на наборном полотне.
— Сколько цифр пригласила Мадина?
— Сколько вышло пирожков?
(Расставить под цифрами,)
— Поровну ли пирожков и цифр?
— Какому не достался пирожок?
(Числу 10,)
— Почему?
— Что больше: 9 или 10?
— Что нужно сделать, чтобы цифр и пирожков стало поровну?
— Если к десяти добавить единицу, получится 10.
— Но вот Мадина несет еще один пирожок и говорит:

— Дадим пирожок цифре 10.

— Сколько стало пирожков?
— Как получилось число 10?
Физминутка. «Как живешь?»

Как живешь?
Вот так!
А плывешь?
Вот так!
— Как бежишь?
— Вот так!
— Вдаль глядишь?
— Вот так!
— Ждешь обед?
— Вот так!
— Машешь вслед?
— Вот так!
— Утром спишь?
— Вот так!
— А шалишь?
— Вот так!

IV.
— Теперь Мадина знает все цифры и все могла сосчитать.
— А вы сможете?
— Я вам буду говорить, кого Мадина видела в зоопарке, а вы
выкладывать счетными палочками на столах.

Вывешивается схема к стихотворению В. Орлова « Я считаю»
«Все, что вижу во дворе я,
Все, что вижу на пути,
Я умею, я умею
Сосчитать до десяти.
Еду с мамой в зоосад
И считаю всех подряд.
Пробегает дикобраз
Это раз.
Чистит перышки сова
Это два.
Третьей стала росомаха,
А четвертой черепаха.
Серый волк улегся спать

Это пять.
Попугай в листве густой
Он шестой.
Вот лосенок рядом с лосем
Это будет семь и восемь.
Девять — это бегемот.
Рот как бабушкин комод.
В клетке ходит лен косматый.
Он последний, он десятый.
Дальше мне не сосчитать —
Надо снова начинать!

Вопросы:
— Сколько зверей встретила Мадина в зоосаде? (счет все вместе)
— Сколько палочек вы выложили на столах? (дети считают каждый у себя на столе,).
— Покажи это число?
— После какого числа стоит цифра 10?
— Какой зверь был последним?
— Какой он по счету?
— Кого увидела Мадина в начале?
— Какой он был по счету?
— Кто был девятым?
— Каким по счету был попугай?
— Мы посчитали всех животных, а что останется если все животные вернутся в зоопарк?
— Можно ли это обозначить какой — то цифрой?

Работа с карточками. (резерв)
— Вставить пропущенные цифры в пустые клеточки.

Итог занятия.
— С какими цифрами мы познакомились сегодня?
— Где в числовом ряду стоит цифра 0, а где 10?
— Из каких цифр состоит цифра 10?
— Кто может посчитать от 0 до 10?

число и цифра 0

число и цифра 0

Подготовила и провела учитель начальных классов Конарева Людмила Борисовна

ТЕМА УРОКА: ЧИСЛО И ЦИФРА 0.

 

ТИП УРОКА:

УРОК ОТКРЫТИЯ НОВОГО ЗНАНИЯ.

 

ЦЕЛИ: ДАТЬ УЧАЩИМСЯ ПРЕДСТАВЛЕНИЕ, КАК ОБРАЗУЕТСЯ ЧИСЛО НОЛЬ, НАУЧИТЬ ПИСАТЬ ЦИФРУ НОЛЬ; ПРОДОЛЖИТЬРАБОТУ НАД НУМЕРАЦИЕЙ ЧИСЕЛ; УЧИТЬ СРАВНИВАТЬ НАСКОЛЬКО В ОДНОЙ ГРУППЕ ПРЕДМЕТОВ БОЛЬШЕ (МЕНЬШЕ), ЧЕМ В ДРУГОЙ.

 

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ:

ОБУЧАЮЩИЕСЯ НАУЧАТСЯ НАХОДИТЬ МЕСТА ЧИСЛА НОЛЬ В ЧИСЛОВОМ РЯДУ, СООТНОСИТЬ ЦИФРУ И ЧИСЛО, ПРИМЕНЯТЬ НАВЫКИ СЧЁТА ЗНАНИЕ СОСТАВА ЧИСЕЛ; УСТАНАВЛИВАТЬ АНАЛОГИИ И ПРИЧИННО-СЛЕДСТВЕННЫЕ СВЯЗИ, ДЕЛАТЬ ВЫВОДЫ; РАБОТАТЬ В ГРУППЕ, СЛУШАТЬ СОБЕСЕДНИКА И ВЕСТИ ДИАЛОГ, СЛУШАТЬ УЧИТЕЛЯ И ВЫПОЛНЯТЬ ЕГО ТРЕБОВАНИЯ.

 

ХОД УРОКА:

 

1. Мотивация к учебной деятельности.

Давайте, ребята, учится считать:

Делить, умножать, прибавлять, вычитать.

Запомните всё, что без точного счёта

Не сдвинется с места любая работа.

Без счёта не будет на улице света,

Без счёта не может подняться ракета,

Без счёта письмо не найдёт адресата

И в прятки сыграть не сумеют ребята.

Беритесь, ребята, скорей за работу!

Учитесь считать, чтоб не сбиться со счёту.

 

 

2. Актуализация знаний и фиксация затруднения в пробном действии.

 

-Какое сегодня число?

-Какое число было вчера?

-Какое число будет завтра?

 

-Мама поставила на стол для своих детей 2 тарелки с супом и 2 тарелки с кашей. Дети поели и ушли. Сколько тарелок осталось на столе?

 

-На кустике клубники было 6 ягод. 3 ягоды покраснели. Сколько ягод стало на кусте?

 

-Купили 2 стола и 7 стульев. Сколько надо докупить стульев, чтобы у каждого стола стало по 4 стула?

 

-А сейчас, ребята, возьмите карточку.

-Что надо в ней сделать? (расставить символы по образцу)

-Кто сделает, поднимает руку.

-Когда я скажу «стоп» ручки положите на стол.

 

3. Выявление места и причины затруднения.

 

-Возьмите карандаши и сверьте свою работу с правильными ответами. Неправильный символ зачеркните.

Слайд №1.

 

4. Построение проекта и выхода из затруднения.

 

Слайд №2

 

-Посмотрите на экран. Сколько яблок на тарелке справа?

-Слева?

-Где яблок больше?

-Что это значит? (3>2)

-Или 2

-А если бы мы не умели считать, как можно было сравнить количество предметов? (брать парами)

-Убираем парами.

-А теперь мы видим, что на тарелке слева осталось одно яблоко, значит, правильно вы сказали 3.

-А что осталось на тарелке справа? (ничего)

-В том случае, когда нет предметов, ни одного не остаётся, обозначают

цифрой 0.

-И так, как вы думаете, о чём сегодня мы будем говорить на уроке?

 

-А теперь подумайте, что больше 0 или 1? (0 меньше 1, т. к. обозначает пустое место, а цифра 1 обозначает 1 предмет).

-А если бы вместо цифры 1 была бы цифра 2 или 3? (любое число было бы больше 0).

-Значит любое число больше ноля.

-Где мы с вами поставим новую цифру на числовом луче?

-На что похож ноль?

 

Ноль собой весьма хорош,

На бараночку похож,

И на бублик, и на шар,

И на круглый самовар.

Нолик дружит с Колобком,

Жить не скучно им вдвоём.

Круглый шарик надувают,

Круглый год на нём летают.

 

Физминутка.

 

Мы похлопаем в ладоши

Дружно, веселее.

Наши ножки постучали

Дружно и сильнее.

По коленочкам ударим

Тише, тише, тише.

Наши ручки поднимайтесь

Выше, выше, выше.

Наши ручки закружились,

Ниже опустились,

Завертелись, завертелись и

Остановились.

 

 

Подготовка рук.

 

-А теперь возьмите карточку. Приготовьте два карандаша, синий и красный.

Найдите цифру, которую мы изучили. Раскрасьте в верхнем правом углу цифру 0 в синий цвет, а в нижнем левом углу в красный цвет.

 

-Проверьте, так ли вы сделали. Слайд №3.

 

5. Реализация построенного проекта.

 

-Рассмотрите в учебнике образец написания цифры ноль (проговариванием).

-Показ учителем на доске.

-Работа в тетради (№1 стр. 26 )

 

 

6. Первичное закрепление во внешней речи.

 

Арифметический диктант.

 

-Давайте вспомним, что значит увеличить? Уменьшить?

 

2 увеличить на 1,

6 уменьшить на 2,

На 1 больше, чем 9

Число, которое при счёте стоит перед 9,

Число, которое стоит после 4,

Число, которое стоит между 6 и 8,

Соседей числа 1.

 

-Проверьте, так ли вы написали?

 

Слайд №4

3 4 10 8 5 7 0 2

 

-Напишите эти числа в порядке возрастания. Начинаем писать с какого числа?

 

0 2 3 4 5 7 8 10

-Проверьте, так ли вы написали?

 

Слайд №5

 

-Какие числа пропущены?

 

Гимнастика для глаз.

 

7. Включение в систему знаний и повторение.

 

-Откройте учебник на стр.70.

 

-На какой главный вопрос мы должны ответить на уроке?

-Ответили мы с вами на этот вопрос?

 

-Рассмотрите картинки ниже.

-Какое из равенств, приведенных справа, к ним подходит? (5-5=0)

-Составьте рассказ к этому равенству.

-Составьте рассказ к двум другим равенствам.

-Какой можно сделать вывод?

 

-Рассмотрите следующий рисунок.

 

-Сколько было листочков на веточке? (3)

-Что потом случилось?

-Один улетел.

-Сколько осталось? (2)

-Как это записали? (3-1=2)

-Увеличилось или уменьшилось количество листочков?

-Уменьшилось.

-Сколько листочков осталось на веточке, когда ещё один листочек упал? (1)

-Как это записали? (2-1=1)

-Сколько осталось листочков, когда упал последний листок? (0)

-Как это записать? (1-1=0)

 

 

Составим рассказ и запись по рисунку на стр. 71. Работа в парах. Один составляет рассказ, другой запись.

-Какой рассказ составили?

-Какая запись получилась?

-Оцените себя. Встаньте, кто сделал точно также, встаньте те кто немного ошибся.

 

-Прочитайте записи ниже двумя способами.

-Прочитайте неравенство.

 

Рассмотрите чертёж.

-Сколько на нём ломаных?

-Сколько многоугольников?

-Как называются эти многоугольники?

 

8. Самостоятельная работа с самопроверкой по эталону.

 

-Прочитайте примеры, которые вы видите на экране.

 

Слайд №6

 

8+1       7-0

 

7+0       3+2

 

2+4       6+1

-Выпиши примеры с ответом 7.

-Проверь, так ли вы сделали.

-Для тех, кто выполнил задание, проверяем

.

Слайд №7

 

-Заполните пропуски в примерах.

 

Слайд №8

 

 

3                     =5

 

 

 

4                     =3

 

 

 

2                 =0

 

 

 

-Проверьте, так ли вы сделали.

 

Слайд №9

 

3+2=5

 

4-1=3

 

2-2=0

 

 

9. Рефлексия учебной деятельности.

 

-Работа по учебнику «Проверь себя» стр.71

 

-Что интересного вы узнали на уроке?

 

-С чем познакомились?

 

-Что запомнили?

 

-Где вам может пригодиться это число?

 

10. Домашнее задание (по желанию)

-Нарисовать цифру 0 в виде разных предметов: лужи, солнышка, баранки, обруча.

-«Оживить» цифру 0.

 

 

 

 

Открытое занятие «Число и цифра 0»

Тема занятия: «Число и цифра 0».

Дата и время проведения: 21 ноября 2017 года, 17.00.

Место проведения: ЦДТ кабинет 28.

Возраст детей 5 лет.

Второй год обучения.

Цель занятия: познакомить с числом и цифрой 0.

Задачи занятия: формировать представление о числе и цифре 0,

закреплять умение сравнивать числа с помощью знаков «больше»,«меньше», «равно»,

развивать пространственные представления,

воспитывать усидчивость.

Оборудование

у педагога: четыре кубика и одна пирамидка, магнитные цифры, рисунки для игры «Фотограф», рисунки деревьев осенью и зимой,

у детей: математический набор, веер цифр, счётные палочки.

План-конспект занятия

1. Организационный момент. Приветствие.

2. Порядковый счет.Закрепление пройденного.

Работа с математическим набором.

-Возьмите из набора 4 квадрата и один треугольник, а у меня на полочке 4 кубика и одна пирамидка.

-Поставьте треугольник вторым по счёту, предпоследней, четвёртой, последней.

3. Работа над темой урока.

Игра «День и ночь».

-Закройте глаза (убираю два кубика), открывайте, что изменилось? (убрали два кубика , осталось три фигуры)

теперь можно сказать? (ничего е осталось, ноль фигур

-Сегодня мы говорим об этом числе и о цифре 0.

Если что-то вдруг пропало,

Улетело, убежало,

Мы, дружок, с тобою вместе

Ставим ноль на этом месте.

-Посмотрите и скажите чего у нас в комнате ноль?

-Давайте познакомимся и с цифрой 0, на что она похожа? (на овал, на букву О и т.п.)

-Круглый ноль, такой хорошенький, но не значит ничегошеньки.

-Найдите цифру в своем математическом наборе. Покажите её.

-Давайте определим место нашей цифре в числовом ряду. На доске магнитные цифры.

-Куда же поставим ноль? (перед единицей)

-Какие соседи у цифры один? (ноль и два).

4. Закрепление пройденного. Работа с веером цифр.

-Покажите соседей числа 3, 1, 4,2.

Работа у доски. Поставь знак =

Запись на доске:

4_3 2_5 0_1 5_0 1_1 4_4 1_0 0_3 5_3 2_4

Физкультминутка.

Речедвигательная игра «Как живёшь?»

Игра на внимание «Нос-ухо».

5.Задание на логическое мышление. Что сначала, что потом.

На доске три рисунка.

-Какое время года на рисунках? (осень, потому что листья красные)

-Как вы думаете, какой рисунок расположить первым, где пять листьев, один или ноль?

На доске ещё три рисунка.

-Какое здесь время года? (весна)

-Как здесь расположить рисунки? (сначала ноль листочков, потом один, а потом пять)

6.Закрепление нового материала.

-Я буду задавать вопросы, говорите ответ хором, но будьте очень внимательны, если ответ ноль, то поднимите нужную цифру:

-Сколько крыльев у петуха?

-Сколько крыльев у слона?

-Сколько рогов у двух козлов?

-Сколько рогов у двух котов?

-Сколько рук у паросенка?

-Сколько ласт у жеребенка?

-Сколько гребней у моржа?

-Сколько ног у карася?

-Сколько пятачков у хрюшки?

-Сколько ушек у подушки?

Физкультурная минутка.

Игра «Карлики-великаны», игра «День и ночь».

7 Работа со счетными палочками.

Игра «Фотограф».

-Приготовьте 7 палочек и постарайтесь выложить по памяти такие же фигуры, какие увидите на доске, будьте предельно внимательны. Рисунки демонстрируются несколько секунд, после чего дети по памяти воспроизводят рисунок используя палочки.

Выкладывание фигуры под диктовку.

-Положите одну палочку вертикально, как у меня на доске, затем одну палочку вправо, одну вверх, одну вправо, одну вниз, одну вправо, одну вниз, три влево.

-На что похожа наша фигура? (пароход, машинка).

-Поднимите руки у кого получилось.

-Вам потребовалось ноль внимания или много внимания? (много)

5. Подведение итогов занятия.

Цифра 0 стихи — Математика для детей Мама7я

Стих про цифру 0

***
Ноль не значит ничего,
Но нельзя и без него.
Без нуля не обойтись,
Ты писать его учись.
Ты уже нарисовал
Аккуратненький овал?
Нету проще ничего:
Ноль похож на букву «О».

***

А в строю-то им раздолье…
Ой, совсем забыл про ноль я!
Так его и нету, вроде,
Хоть и водится в природе.

***

Ноль собой весьма хорош:
На бараночку похож,
И на бублик, и на шар,
И на круглый самовар.

Нолик дружит с колобком,
Жить нескучно им вдвоем.
Круглый шарик надувают,
Круглый год на нем летают

Стихи про цифру ноль

***

Ноль и нуль — одно и тоже.
Нуль, как цифра — пустота!
Нуль пощупать каждый может,
Пробуй сам, пожалуйста!
Присмотрись к велосипеду,
У него есть два нуля.
На нулях к реке поеду
Через рощу и поля.
Хулахуп кручу руками.
Посмотреть сюда изволь.
Талией кручу, ногами
Обруч, словно цифру ноль.

***
Нолик — круглый,
Как Земля.
Все считают от нуля.
Арифметика проста:
Если ноль — ладонь пуста.
Пишем «0»,
И ясно всем:
Здесь чего-то нет совсем!

***

Цифра нуль — пустое место
Или просто — ничего.
Нуль раздулся в знак протеста,
Чтоб заметили его.
Нулик! Нуль! Не надо злиться.
Стань скорей за единицей.
Только так, когда вы вместе,
Будет сразу целых — десять!

***

А вчера пришли подружки,
Мне баранки принесли,
Бублики большие, сушки —
Все съедобные нули!
Есть кругом нули. Быть может,
И другие цифры есть.
Мне приятней нулик всё же,
Нулик-пончик можно съесть.
И ещё есть нуль, не спорю,
Ноль я на море видал.
Ходят корабли по морю,
И у них есть ноль-штурвал.
Есть «обувка» у машины.
Этим нуликам я рад.
Нулики — четыре шины —
Целы? Значит, едем в сад!

***
Нуль, запомни, детвора, —
Лишь от бублика дыра.
Бублик сделали из теста.
Вот мы скушали его.
Рузультат — пустое место,
Не осталось ничего.
Ничего нет, в самом деле.
Нуль никак не сосчитать.
Этим бубликом, что съели,
Будем нуль обозначать.

Подписывайтесь на блог автора сайта
@mama7ya.ru

***

На горшке сидит король,
Ищет всюду цифру ноль.
Можем подсказать ответ:
Ноль — когда чего-то нет!

***

Я оранжевый овал
На листе нарисовал.
У него большая роль,
Так как это цифра Ноль.

***
Ноль похож на букву О,
Он не значит ничего.
Но любую цифру враз
Увеличит в десять раз.

***

Вы не встретите миногу,
Чтоб плыла в строю не в ногу.
Почему? Да, просто ног
Ровно НОЛЬ у рыб миног

***
Нуль — число, не пустота,
Сила в нём и красота.
Нуль всегда всё округляет
И на числа так влияет,
Что из хилой единицы
Десять может получиться,
Если шесть нулей добавить,
Миллионом кол вдруг станет —
Удесятеряет числа
Нуль, как цифра, очень быстро.
Но бывает нуль другой —
Человек с ним не герой,
Тот, кто трусоват, ничтожен
Очень он с нулём похожий —
Нуль без палочки, пустышка,
Неприметный, даже слишком.
Если говорят «ты нуль»,
Это хуже вражьих пуль.
Будь хотя бы единицей,
А за ней ставь вереницей
Несколько нулей подряд,
И тогда сам будешь рад,
Что не стал ты пуст и кругл,
Как тот одиночка нуль.

***
Ноль похож на колобок,
Он пузат и круглобок.
На него похожа Кошка,
Если сложится в клубок.

***

Ноль — задумчивый мудрец.
Где начало, где конец
Сам не может разобрать.
Как его нам не узнать!

***
ДО-РЕ-МИ-ФА-СОЛЬ-ЛЯ-СОЛЬ
Что за цифра этот ноль?
Если ноль, то значит пусто.
Ноль конфет — нам очень грустно.
А вот если ноль проблем,
Это нравится нам всем.
***
Сколько лет в яйце цыпленку,
Сколько крыльев у котенка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра… 0.
***
Вот это ноль иль ничего.
Послушай сказку про него.

Подписывайтесь на блог автора сайта
@mama7ya.ru

Стих про цифру 0 для 1 класса

***

Скок да скок,
Скок да скок 
Покатился колобок,
Круглый да румяный,
Прямо на поляну.
Нам колобок
Нарисовать,
Как ноль в тетради
Написать.
Да только ноль
Не колобок,
А просто он
Пустой кружок.

***

Скачет мяч по всем страницам,
Ищет ноль свою сестрицу.
Он имеет вид кольца,
Без начала и конца.
А если встретит сестрицу свою
То станет он числом, а не цифрой.

***

Сказал веселый, круглый ноль
Соседке-единице:
— С тобою рядышком позволь
Стоять мне на странице

Она окинула его
Сердитым, гордым взглядом:
— Ты, ноль, не стоишь ничего.
Не стой со мною рядом!

Ответил ноль: — Я признаю,
Что ничего не стою,
Но можешь стать ты десятью,
Коль буду я с тобою.

Так одинока ты сейчас,
Мала и худощава,
Но будешь больше в десять раз,
Когда я стану справа.

Напрасно думают, что ноль
Играет маленькую роль.

Мы двойку в двадцать превратим.
Из троек и четверок
Мы можем, если захотим,
Составить тридцать, сорок.

Пусть говорят, что мы ничто, —
С двумя нолями вместе
Из единицы выйдет сто,
Из двойки — целых двести!

***

И  значит цифра эта,
Что ничего здесь нету.
И звери съели колобок.
Вот что такое
Ноль- кружок.

***

Ноль на месте на пустом
Ставят, как известно,
Только он при всем при том
На пустое место.
Коль ноль к числу ты прибавляешь
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав как множитель средь чисел,
Он сводит мигом всех на нет,
И потому в произведении
Один за всех несет ответ.
Ноль без палочки –место пустое,
Помни правило это простое.
Ноль – Король, если палочка слева
Встанет рядышком как Королева.

Стих про цифру ноль для детей

***

Эту цифру знать изволь: 
На баранку похож ноль. 
Ноль похож на колобок. 
Он пузат и круглобок. 
На него похожа кошка, 
Если сложится в клубок.

***

Ноль не значит ничего.
Очень жалко мне его.
Он хороший: круглый, гладкий,
Всё с подсчётами в порядке.
Ноль со всеми очень дружен,
Он везде и всюду нужен.
Ноль не требует наград,
Завершает цифр ряд.

Подписывайтесь на блог автора сайта
@mama7ya.ru

***

Могу назвать его мячом,
А хочешь дыркой назовем,
А можно бубликом,
 Почти что кругленьким.
Но как его не назовем,
 Он называется нулем!

***

Папа чай пил спозаранку,
Аппетитно  ел баранки.
Сын баранку взял из плошки,
Призадумался немножко,
Отогнал рукою моль
и сказал : -«Она  как НОЛЬ!.
Если ноль на стол положишь,
То и съесть его не сможешь.
Ноль – ничто, пустое место,
Ни картина и не тесто,
Ничего : ни мед, ни мел…»
…Что же папа с чаем съел?

Нолик дружит с единицей,

Хочет даже породниться

Вместе с нею – он число!

Сам не значит ничего.

Смотрите также:

Всё про цифру 0:

Подписывайтесь на блог автора сайта
@mama7ya.ru

Умка (платная)

Планируемые результаты.

По направлению «Подготовка к обучению грамоте» к концу учебного года ребенок должен:

— Знать буквы русского алфавита

— Писать буквы русского алфавита в клетке

— Понимать и использовать в речи термины «звук», «буква»

— Определять место звука в слове в начале, в середине и в конце

— Различать гласные, согласные, твердые и мягкие согласные, звонкие и глухие согласные звуки

— Пользоваться графическим обозначением звуков (гласные – красный квадрат, твердые согласные – синий квадрат, мягкие согласные – зеленый квадрат)

— Соотносить звук и букву

— Определять ударный слог, ударную гласную и обозначать соответствующим значком

— Проводить звуковой анализ слов

— Читать слова, слоги, предложения

— Правильно пользоваться терминами «звук», «слог», «слово», «предложение»

 По направлению «Математическое развитие» к концу учебного года ребенок должен уметь:

— Выделять и выражать в речи признаки сходства и различия отдельных предметов и совокупностей.

— Объединять группы предметов, выделять часть, устанавливать взаимосвязь между частью и целым.

— Находить части целого и целое по известным частям.

— Сравнивать группы предметов по количеству с помощью составления пар, уравнивать их двумя способами.

— Считать в пределах 10 в прямом и обратном порядке, правильно пользоваться порядковыми и количественными числительными.

— Сравнивать, опираясь на наглядность, рядом стоящие числа в пределах 10.

— Называть для каждого числа в пределах 10 предыдущее и последующее числа.

— Определять состав чисел первого десятка на основе предметных действий.

— Соотносить цифру с количеством предметов.

— Измерять длину предметов непосредственно и с помощью мерки, располагать предметы в порядке увеличения и в порядке уменьшения их длины, ширины, высоты.

— Узнавать и называть квадрат, круг, треугольник, прямоугольник, цилиндр, конус, пирамиду и находить в окружающей обстановке предметы, сходные по форме.

— В простейших случаях разбивать фигуры на несколько частей и составлять целые фигуры из этих частей.

— Выражать словами местонахождение предмета, ориентироваться на листе клетчатой бумаги (вверху, внизу, справа, слева, посередине).

— Называть части суток, последовательность дней в неделе, последовательность месяцев в году.

Преподавание детям числа ноль: занятия для дошкольников и идеи уроков

Понятие нуля обычно сложнее, чем счет и другие ранние представления о числах. Таким образом, мы обычно вводим его только после того, как ребенок до некоторой степени понял значение чисел. Разница между 0 и другими числами заключается в том, что все остальные числа имеют осязаемую визуальную форму, а 0 — нет.

Некоторым детям действительно трудно понять, что 0 ничего не значит. Вот несколько дошкольных заданий с нулевым номером, которые вы можете использовать, чтобы научить и укрепить концепцию нуля.Сначала мы связываем число 0 с пустым и ничем и постепенно помогаем им понять связь 0 с другими числами.

Чаши и карточки с цифрами

Сделайте несколько карточек с 0 на них. Возьмите набор из 8-10 чаш и разложите их в линию. В несколько мисок поместите конфету или любой другой предмет. Ребенку нужно положить карту с номером 0 перед пустыми мисками.

Бумажные стаканчики и веточки листьев

Для этого упражнения наполните бумажные стаканчики песком и поместите 8-10 из них в ряд.В каждую чашку поместите веточку с листьями, чтобы получились миниатюрные елочки. На некоторых деревьях удалите все листья. Ребенок должен положить карту с номером 0 перед деревьями, у которых нет листьев.

Картины «Деревья с яблоками»

Это задание можно сделать на доске объявлений, в виде белой доски или даже в виде рабочего листа. Нарисуйте или сделайте набор деревьев. Внутри некоторых деревьев нарисуйте яблоки. Ребенок должен написать цифру 0 под деревьями, на которых нет яблок.

Счетчики

Это задание очень легко сделать, и оно не требует места.Держите много пенсов или даже фишек шашек для этого занятия. На листе бумаги нарисуйте сетку из квадратов. Внутри каждого квадрата напишите число от 0 до 5. Ребенок должен увидеть это число и положить на него нужное количество монет. На квадраты, на которых написано 0, ребенок не должен ставить монеты.

Ступеньки

Вот еще одна игра, которая поможет детям понять число 0. Дети должны начинать с вершины лестницы. Когда вы говорите «один», ребенок должен прыгнуть на одну ступеньку ниже.Если вы называете «ноль», ребенок должен оставаться на месте. Если ребенок уходит, когда вы называете 0, он выбывает из игры. Таким образом, дети должны стараться оставаться в игре, пока не достигнут подножия лестницы.

Таким образом, это некоторые дошкольные занятия номер ноль, которые вы можете использовать. Вот еще несколько идей для обучения математике с помощью упражнений. Если у вас есть идеи для добавления, оставьте их в разделе комментариев ниже.

40 Потрясающие упражнения с числами для дошкольников

Всегда есть , что мы можем открыть для себя, а также старые любимые.Я так благодарен за то, что нам вручили задания … Веселые и простые, которые можно объединить в мгновение ока! Ты потрясающий, Джейми, и я ценю, что ты делишься своими делами и идеями !! — Мелисса К.

«Мне очень нравится, что этот снимает с себя всю подготовительную работу по привлечению моих детей. Так легко просто повесить календарь и взглянуть на него для вдохновения, когда мы в фанке». — Участник Activity Room, Рэйчел

Я обнаружил, что невозможно найти в Google идеи с миллиона разных сайтов, организовать себя, купить расходные материалы и т. Д. Это именно то, что я искал! Спасибо за то, что сделали что-то настолько организованное и простое в использовании. — Пользователь планов действий на ранний период, Мелисса К.

Это избавляет от необходимости рыскать по Интернету в поисках идей. Это похоже на поиск рецепта в Интернете, где так много вариантов, что часто бывает не так утомительно смотреть в книгу на полке, чем беспокоиться о слишком большом количестве вариантов. — Пользователь планов действий в первые годы, Робин Дж.

Большое спасибо за эту деятельность.Они доказали мне, что Я МОГУ быть той мамой, которая делает крутые и творческие вещи со своими детьми! И эти крутые и креативные вещи могут быть довольно простыми! Какое откровение. Спасибо!! — 7 Day Challenge, Кэти М.

Я чувствую себя молодой мамой, у которой так много забавных идей. Раньше я боялся полудня, после сна, так как было так скучно делать одно и то же изо дня в день, но теперь я с нетерпением жду нашего «игрового» времени! — Хейли С.

Вы изменили то, как я провожу время со своим ребенком, во многих положительных аспектах! Теперь я один счастливый папа, который больше не задается вопросом, что я собираюсь делать с этим маленьким парнем в течение следующих 12 часов: P Ваш сайт впервые стал спасением жизни папы! — Джек С.

Трудно придумать что-то, что могло бы развлечь и увлечь трехлетнего ребенка, заботясь о ребенке. Все, что мы до сих пор пробовали на вашем сайте, понравилось трехлетнему ребенку. Ваши идеи настолько просты, что он может воплощать их в жизнь часами. НЕБЕСА! — Карен И.

Детский сад: нулевой урок, мой герой! Изучение Number Zero

В этой части урока я использую SMART Board. Если у вас есть SMART Board, файл Number Zero Notebook можно легко загрузить и открыть.Если у вас есть интерактивная доска другого типа, вы все равно можете использовать этот урок, открыв файл в Smart Notebook Express. Также есть PDF-файл со слайдами, чтобы вы могли воссоздать эту часть урока.

Я собираю своих учеников перед SMART Board. У меня есть карточки с именами каждого ученика. Эти карточки используются для выбора участников SMART Board.

Я открываю первый слайд (слайд SMART Board 1), на котором цель урока написана «удобными для учащихся» терминами.Есть цель содержания и цель языка, чтобы помочь сосредоточиться на расширении словарного запаса для моих изучающих английский язык (EL), чтобы соответствовать методам обучения SIOP. Я зачитываю эти цели своим ученикам.

Content Objective
Я могу найти нулевое число, определить, когда в группе будет ноль элементов, и удалить элементы из группы, пока не останется ноль элементов.

Языковая цель
Я могу использовать число ноль, чтобы сообщить другу, сколько элементов находится в группе.

Затем я перехожу к слайдам.

Слайд 2: Это число 0.

Слайд третий: Когда я считаю, ноль может быть первым числом, которое я говорю. Затем я считаю, указывая на числа на слайде Smartboard. Я повторяю, чтобы студенты считали со мной.

Слайд четвертый: Мне нечего трогать. Считать нечего. В коробке ноль вещей. Когда НЕТ — НУЛЬ.

Слайд 5: У меня есть несколько групп элементов на этой странице. Мне интересно, какие у них ноль. Можете ли вы подойти и найти группу, в которой нет предметов. Сотрите, чтобы проверить.

Я звоню студентам с помощью своих «карточек выбора». После того, как ученики находят те, у которых есть ноль. Когда ученики находят группу с нулем, мы говорим о том, что им нечего трогать при счете. Студенты стирают в круге, чтобы получить цифру ноль.

После того, как ученики отождествляют наборы с нулем, я спрашиваю их, сколько объектов находится в других группах. Я прошу их подойти к доске и продемонстрировать счет предметов. Остальные объекты имеют восемь и девять объектов для проверки этих чисел. Я убеждаюсь, что ученики демонстрируют прикосновение и счет каждого объекта.

Slide Six and Seven: Теперь у учащихся есть возможность убирать элементы из группы, пока не останется ноль. На шестом слайде ученики снимают игрушки с коврика и кладут их в коробку для игрушек.

Учащиеся пальцем перетаскивают каждую игрушку в коробку (использование гладкой части ногтя хорошо помогает учащимся перемещать предметы. Если это слишком сложно, учащиеся могут использовать теннисный мяч, чтобы перетащить предметы на SMART. Доска). Когда они закончили, мы обсуждаем, остались ли какие-нибудь предметы. Я говорю: . Мы знаем, что объектов нет, потому что нечего трогать и считать. Мы делаем то же самое на седьмом слайде с печеньем.

Слайд восемь : Я использую этот слайд, чтобы продемонстрировать, как сделать ноль. Я подчеркиваю важность начала числа сверху, где находится зеленый кружок или кружок «вперед». Я показываю, как составить число, говоря ученикам: Начните сверху, где находится зеленая точка, поверните влево, коснитесь нижней линии и поверните вверх. Закройте верх.

Slide Nine: Теперь пора заняться Turn and Talk, чтобы развить навыки устной речи.Студенты получают задание со своими партнерами Turn and Talk. Я говорю студентам: Теперь повернитесь к другу и скажите им, сколько кузнечиков там.

После того, как студенты имели возможность поговорить, я прошу студентов поднять руку, если они знают, сколько кузнечиков там. (Их девять, чтобы помочь пересмотреть это число). Когда я получаю правильный ответ, я прошу их повторить ответ целым предложением, чтобы расширить их языковые навыки. Я говорю: Вы правы.Есть девять кузнечиков. Затем я прошу их повторять за мной: «Есть девять кузнечиков».

Теперь я сосредотачиваю внимание студентов на следующей группе. Спрашиваю, сколько там игрушек. Обычно это вызывает хихиканье. После разговора со своим партнером я спрашиваю, знает ли кто-нибудь ответ. Верно. Нет игрушек ноль. Я знаю, что их ноль, потому что мне нечего трогать и считать. Скажи это со мной. Нет игрушек ноль.

Затем мы переходим от SMART Board обратно к нашим столам.

«Место, оценка и порядок величины»

Спросите ребенка, что такое «ноль», и он ответит либо «число», либо «ничего». Но ноль — это гораздо больше, чем просто «число» и «ничто». Этот блок « Удивительный ноль в главной роли, место, оценка и порядок величины » покажет детям, насколько важно число ноль в математике. Особое внимание будет уделено использованию нуля в нашей десятизначной системе значений для записи чисел.Также будет рассмотрено, как числа с множеством нулей, круглые числа помогают нам в оценке, концентрируя наше внимание на относительных размерах чисел, а не загипнотизированных их цифрами. Единица начинается с важности нуля в разряде, а затем заканчивается важностью нуля по порядку величины в реальных жизненных ситуациях, таких как сложение и вычитание. Основная цель этого подразделения — заложить прочный фундамент концепции Ордена Величины. В пределах порядка величины попадают концепции разряда, заполнителя, где ноль является главным персонажем в сценарии.

Мы считаем, что в государственных школах Питтсбурга все учащиеся способны разбираться в математике. Классная среда уважительно относится ко всем идеям; учащимся предлагается рисковать, поскольку возникают проблемы и учащиеся пытаются найти решения. Основное внимание уделяется учащимся, которые выясняют ситуацию, проверяют идеи и делают предположения, развивают причины и предлагают решения. Студенты делятся и обсуждают в группах, парах и индивидуально. Приветствуются рассуждения и упорный труд, поскольку учащиеся отстаивают свои методы и обосновывают решения.В государственных школах Питтсбурга учащиеся формируют понимание и развивают навыки на собственном опыте. Математика имеет большее значение, когда она основана на реальных жизненных контекстах и ​​ситуациях. Дети начинают школу с большими математическими знаниями и интуицией, чем считалось ранее. Наша программа строится на этом и постепенно переводит детей от конкретного понимания к абстрактному и символическому. Овладение математическими понятиями и навыками приходит с многократным повторением и практикой, а не после одного урока.Это позволяет учащимся устанавливать новые связи и использовать уже известный математический материал, постепенно изучая более сложный и интересный материал. Все учащиеся государственных школ Питтсбурга имеют возможность получить математические возможности или стать математически грамотными. Предоставляя возможности для улучшения качества жизни, он расширяет выбор личных и профессиональных жизненных путей. Наша цель — предоставить высококачественную учебную программу, которая позволит учащимся справляться с математическими задачами, с которыми они столкнутся в будущем. ¹

Моя школа расположена в одном из районов Питтсбурга с самым высоким уровнем преступности и бедности. По соседству царит нестабильность, и большинство семей — нетрадиционные. Многие дети ходят в школу за стабильностью, горячим обедом и общением. Моя школа — это центр от детского сада до восьмого класса, где в среднем учатся 250 учеников, из которых 99,2% — афроамериканцы. Дисциплина в здании очень строгая и требует, чтобы каждый ребенок носил униформу.Размер класса составляет от пятнадцати до двадцати пяти детей. Текущая программа элементарной математики — это серия «Повседневная математика». Учебная программа по повседневной математике основана на практических занятиях. Уроки проводятся по спиральному методу, при котором дети каждый год узнают немного по какой-либо теме. Дети изучают много важных идей, но как учитель математики в средней школе я обнаружил, что дети приходят в шестой класс с большими пробелами в своих предварительных знаниях основных математических навыков. Их концепции путаются, и у них нет твердой основы математических фактов.Моя работа как учителя третьего класса — дать детям прочную основу, необходимую для успешного обучения. Детям должна быть предоставлена ​​безопасная и благоприятная среда, в которой они могут сосредоточиться на своем образовании. Мне нужно дать им фундамент, который будет вечным.

Мой третий класс основан на положительном самооценке и взаимном уважении ко всем, кто переступает порог. Правила, процедуры, последствия и награды — все это часть моего руководства классом.Многие дети приходят в школу с негативизмом и проблемами, которые влияют не только на их образование, но и на образование их сверстников. Этот модуль необходимо запускать в самый первый день в школе, чтобы сразу же создать атмосферу в классе. В блок встроены позитивная самооценка и поддержка одноклассников. Чтобы дети ходили в школу и учились, они должны быть счастливы и чувствовать себя защищенными от внешних влияний. Я должен нести двойную ответственность за планирование ситуаций и занятий, чтобы облегчить их математическое развитие, при этом я должен быть достаточно гибким, чтобы использовать возможности, случайно возникающие в течение дня, чтобы запечатлеть «обучающие моменты».Одна из моих целей — помочь своим детям стать самостоятельными учениками. Это может произойти только в том случае, если я позволю детям принимать решения и брать на себя ответственность за их обучение. Привлекая своих детей к принятию повседневных решений об оценке их работы и побуждая их ставить и пересматривать личные цели, я могу помочь своему классу стать активными учениками. Самооценка побуждает их задуматься о том, что они делают и что им нужно делать.

Учащиеся начальных классов способны овладеть навыками оценивания, и для этого им нужен инструктаж.Мы все согласимся с тем, что существует большая потребность в мероприятиях, которые приведут учащихся к осознанию и пониманию оценки. Совершенно очевидно, что дети могут успешно оценивать вычислительные решения только в том случае, если они сначала имеют чувство числа, которое формирует основу для решения задач и навыков логического мышления. Оценка играет настолько важную роль во внешкольных учреждениях, что у детей должен быть широкий опыт владения этим навыком. Более 80% ситуаций, связанных с решением проблем вне школы, включают оценку.Я считаю, что тема, которая так широко используется в дальнейшей жизни, не должна рассматриваться как спиральная деятельность. Если у ребенка нет твердой основы с оценкой в ​​очень раннем возрасте, я чувствую, что он будет играть в догонялки на протяжении всего обучения. Спираль не даст немедленного эффекта, необходимого для создания желаемого фундамента.

В итоговом отчете Национальной консультативной группы по математике за 2008 год также говорится: «Целенаправленное, последовательное продвижение обучения математике с упором на владение ключевыми темами должно стать нормой в учебных программах начальной и средней школы.Следует избегать любого подхода, при котором темы постоянно пересматриваются из года в год без завершения. К концу 6-го класса у детей должно быть устойчивое чувство числа. Это чувство числа должно включать понимание разряда и способность составлять и разлагать целые числа. Сильное чувство числа также включает в себя способность оценивать результаты вычислений и, таким образом, оценивать порядок величины, например: сколько людей помещается на стадион или сколько галлонов воды необходимо для заполнения бассейна? »

Я считаю, что полное понимание оценки требует полного внимания, а не просто урока типа «ну, кстати,».Во многих учебных программах, которые я видел, оценка используется как вторичный способ решения проблемы. Например: открытая задача преподается, когда дети показывают свою работу, объясняют свою работу и проверяют свою работу с помощью оценок. Поскольку оценка так важна в повседневной жизни, ее следует научить сначала оценивать ответ, а затем решать проблему обычными способами. Если ответ похож на оценку, значит, проблема должна быть верной. Если сначала найти фигурку в парке, ребенок сможет понять разумность своего ответа.Это твердое убеждение подводит меня к выводу, что каждый урок, данный здесь, нужно продолжать до тех пор, пока он не будет усвоен.

Суета и суета нашего мира высоких технологий оставляет очень мало места для наших детей. Детей постоянно развлекают и стимулируют как активные, так и интерактивные шоу и игры. Они приходят в школу, ожидая того же типа программирования. Когда его не получают, детям становится скучно, у них незавершенные задания, и они страдают в учебе.Если такое отношение начнется в младших классах, то в старших будет намного хуже. Наша работа как учителей — найти занятия, которые будут стимулировать их академические потребности и побудить их стать активными учениками.

Детям любого академического уровня нужно дать время ошибиться, время подумать и время бороться с мыслью о том, что ошибиться с первого раза — это нормально. Если они хотят глубоко погрузиться в математику, у них должно быть достаточно времени, чтобы заняться реальными математическими проблемами.Идеальная ситуация для учителя — это сделать шаг назад и стать фасилитатором. Учитель должен учиться, слушая, что говорят дети. Чтение, ведение дневника и обсуждение в классе должны быть частью каждого урока.

Исследования показывают, что дети начальной школы не понимают нашу систему счисления, особенно числовую ценность (Kamii and Joseph, 1988; Ross, 1986, 1989; Smith, 1973). Согласно исследованию, только 33% третьеклассников знали, что цифра 16 означает 1 десятку и 6 единиц.Но при тщательно спланированных действиях по подсчету и группировке по сотням, десяткам и единицам можно ожидать, что третьеклассник поймет и будет работать с трехзначными и большими числами. ²

Должно быть очевидно, что часто проще рассчитывать с использованием оценок, чем с использованием точных цифр. Менее очевидно, что тогда, даже если калькуляторы и компьютеры избавляют от вычислений, оценка может значительно упростить задачу без существенной потери качества ответов.Фактически, ответы, полученные с использованием точных оценок, могут быть более разумными и более реалистичными, чем те, которые пытаются быть точными. ³

Для того, чтобы ребенок стал успешным математиком, мы, как учителя, должны заложить прочный фундамент не только в базовых навыках сложения, вычитания, умножения и деления, но также и в использовании нуля в качестве заместителя места. , ноль в округлении и ноль по порядку величины, таким образом, используя оценку в качестве инструмента.Учителя начальной школы должны дать ребенку все инструменты, необходимые для достижения успеха. Многие дети думают, что математический инструмент — это калькулятор, линейка, базовые 10 кубиков или циркуль. Дети не осознают, что инструментами могут быть алгоритмы, формулы или просто твердое знание предмета.

Уроки будут созданы таким образом, чтобы пригласить всех учеников на математику — мальчиков и девочек, представителей различных культурных, этнических и языковых групп, а также студентов с разными сильными сторонами и интересами.Этот модуль поможет детям развить удовольствие и понимание математики, развить гибкость и уверенность в подходе к задачам, свободное владение математическими навыками и инструментами для решения задач и умение оценивать свое математическое мышление. Поскольку третий класс, как правило, представляет собой отдельный класс, особое внимание будет уделяться навыкам чтения и письма.

В этом модуле будет использоваться несколько рассказов и песен для закрепления концепции. Детям нужна возможность обдумать и объяснить или обосновать свои идеи и решения как в устной, так и в письменной форме.Детская литература предоставляет контекст, в котором могут быть изучены математические концепции, закономерности, решения проблем и контексты реального мира. Детские книги, посвященные математике, делают математику доступной для всех детей. Поэтому я буду использовать различные книги по математике на протяжении всего модуля. У класса будут письменные или устные размышления или ответы. Чтобы представить решение и написать математически, им необходимо упорядоченно скомпилировать свою информацию.

Важно, чтобы дети находили собственные способы организации и записи своей работы.Им нужно научиться объяснять свои мысли с помощью рисунков и письменных слов, а также как организовать свои результаты так, чтобы их мог понять кто-то другой. По этой причине предполагается, что учитель не всегда предоставляет, например, лист записи для учащихся; если будет предоставлен счетный лист, ребенок автоматически определит проблему с помощью счетчиков, а не найдет свою собственную стратегию. ⁴

Идея небытия и пустоты вдохновляла и озадачивала математиков, физиков и даже философов.Что значит пустое пространство? Если пространство пусто, имеет ли оно какое-либо физическое значение или цель? Использование нуля в оценке может быть трудной для понимания концепцией. Маленькому ребенку нужны постоянные повторения и полное понимание того, что значит оценивать. Процесс важнее точного ответа. Использование реальных жизненных ситуаций, требующих оценок, даст детям возможность привыкнуть к оценке. Оценка создается с использованием предварительных знаний. Каждый становится лучше в оценке с практикой.От школы до супермаркета и многих других мест, чтобы выжить, мы должны совершать точные оценки.

Оценка начинается и заканчивается нулем.

У нуля много задач в математике. В первую очередь, при подсчете цифрой перед единицей всегда будет ноль. При подсчете можно не утверждать, но все знают, что до единицы чего-то не было ничего или нуля. Ноль может превратить двойку в двадцать, а затем в двести. Каждый раз, когда для увеличения числа добавляется ноль, он умножает это число на 10.

Разрядное значение позволяет человеку различать номинал цифры и ее значение из-за его особого положения в цифре. При обучении словарному запасу числовых значений требуются такие слова, как единиц, десятки, сотни, тысячи, десятки тысяч, сотни тысяч и т. Д. Однако ключевой момент, который нужно студентам при оценке, особенно при предварительной оценке, заключается в том, что каждое место в десять раз больше, чем следующее меньшее место.

Порядок величины — это понятие, которое используется в классе, но не раскрывается как таковое в начальных и средних классах.Идея порядка величины основана на степенях десяти. Степень десяти — это десять, умноженная на себя определенное количество раз. Степень десяти записывается как 1, за которой следуют несколько нулей, а количество нулей указывает степень. Таким образом, степени 10 равны 1 = 100, 10 = 101, 100 = 102, 1000 = 103 и так далее. Порядок числа основан на наибольшей степени, равной десяти меньшим числа. Например: 1000 7, 452 10 000, поэтому порядок величины 7 452 равен 3. Чтобы упростить этот пример: порядок величины равен 3, потому что есть 3 цифры, следующие за 7 в 7 452.Чтобы прояснить: 100 256 1000, поэтому порядок 256 равен 2. Упрощенно: порядок величины равен 2, потому что после первых 2 в 256 идут 2 цифры.

Используя показатель степени, можно возвести десятку в любую степень, необходимую для представления размера. Показатель степени может быть положительным, чтобы представлять число больше единицы, или отрицательным числом, чтобы представлять число меньше единицы. 5 равно 1 с 5 нулями или 100000.5 (один доллар двадцать центов, умноженный на десять в пятой степени). Десять в пятой степени будут равны единице и пяти нулям или 100000. умножить на 1,20 доллара, и мои сбережения составят 120 000 долларов. (Если бы!). Если бы размер моего сберегательного счета был равен шести, у меня было бы более миллиона долларов. Порядок величины может иметь бесконечное количество нулей, каждый из которых представляет собой кратное 10. Вау! Этот ноль имеет большую силу.

Рейс (1986) описывает пять стратегий оценки: предварительная оценка, округление, кластеризация, совместимые числа и специальные числа.В этом модуле будут использоваться стратегии начальных и ведущих цифр, но сначала мы начнем с нуля и разряда. Урок округления ведущей цифры совпадет с разработкой концепции порядка величины. Базовые десять блоков будут использоваться, чтобы узнать, насколько легко можно складывать и вычитать, используя расширенную форму. Базовые 10 блоков состоят из единичных кубов (1/2 «x 1/2» x 1/2 «), десяти стержней (1/2» x 1/2 «x 5»), сотен квартир (5 «x 5» x 1/2 дюйма) и тысячи кубиков (5 дюймов x 5 дюймов x 5 дюймов). Эти блоки можно использовать для представления развернутой формы, чтобы дать визуальное представление числа.

Правило для предварительной оценки: Для любого числа в вычислениях: от 1 до 10 округлить до ближайшего целого числа; от 10 до 100 округлить до ближайшего числа, кратного 10; например: выберите из 10, 20,30 ….. 100, от 100 до 1000, округлите до ближайшего числа, кратного 100, 200, 300 и т. д. Примером этого может быть следующий: чтобы сложить 347 + 129, мы сначала складываем сотни (300 + 100), затем десятки (40 + 20), затем единицы (7 + 9), чтобы получить 476.В этом методе используется развернутая форма каждого числа и отдельно добавляются сотни, десятки и единицы. По вертикали эта проблема будет выглядеть так:

347

+ 129

300 + 100 = 400

40 + 20 = 60

7 + 9 = 16

476

Математики из Rutgers заявляют, что точное определение оценки ведущей цифры: «Таким образом, разумное приближение к многозначной сумме или разнице всегда можно сделать, рассматривая только крайние левые места и игнорируя другие.Эта стратегия называется предварительной оценкой и является основной стратегией оценки, которую используют многие взрослые. В третьем и четвертом классах он должен сопровождать традиционные стратегии округления ». ⁵

Первая цифра захватывает большую часть числа, следующая цифра захватывает большую часть того, что осталось, и после этого цифры менее важны с точки зрения размера. В рамках уроков мы обсудим тот факт, что когда вы складываете очень большие числа, относительный размер числа действительно не сильно меняется, когда вы смотрите на каждую цифру.Например: 1,354,596 + 2,485,439 относительно можно округлить до ближайшего миллиона и по-прежнему оставаться в оценочной цифре парка мячей. Здесь мы бы прибавили 1 000 000 + 2 000 000 »3 000 000. Важность нуля здесь очень важна, и на ней следует остановиться.

Ноль часто приравнивается к «ничто», но это плохая аналогия. Ноль может означать отсутствие качества, но также может быть отправной точкой. На числовой прямой ноль находится точно между отрицательным и положительным числами.Ноль — это начальная точка или начало на графике с осью x и осью y. Слово происхождение звучит очень важно. Происхождение есть начало. Ну так и ноль. Это было настолько важно, что математики на самом деле боялись этого и отказывались его использовать. Это приходило и уходило из истории, и действительно трудно определить точный момент создания нуля.

Счет — это универсальная человеческая деятельность. Однако большинство людей не начинают свой счет с нуля. Счет сначала начался, когда люди использовали свои пальцы, чтобы отслеживать, «сколько», даже маленький ребенок может поднять пальцы и сказать: «Меня столько».Что будет, когда тебе исполнится 11? Больше никаких пальцев, возможно, вы могли бы включить пальцы ног, но у нас также нет неограниченного количества пальцев на ногах. Вот почему многие группы людей изобрели свою собственную «Систему подсчета», которая до сих пор широко используется. В этой системе вы делаете небольшую вертикальную линию для одной единицы, затем другую рядом с ней для второй и так далее, пока не дойдете до пятой, которая пересекает другие четыре. Затем вы начинаете повторять следующий подход из пяти повторений. Оказывается, это отличная система для отслеживания небольшого количества объектов с течением времени, когда вам может потребоваться добавить еще один в любое время.Конечно, любой из вас, кто использовал систему подсчета в начальной школе, знает, что многократно подсчитывать несколько тысяч подсчетов быстро становится громоздко. Прошло много веков, прежде чем кто-либо даже подумал о включении нуля в качестве числа.

Чтобы оценить значение нуля при счете, взгляните на десятичную и римскую системы счисления. В десятичной системе все числа состоят из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. После счета до девяти цифры повторяются в различной последовательности, так что любое число можно записать всего десятью цифрами.Также позиция числа указывает значение числа. Например, в 407 4 означает четыре сотни, 0 означает отсутствие десятков и 7 означает семь. В римской системе счисления есть буквы I и V, которые используются в разных количествах и в разном порядке для обозначения 1-8, но на девятке вы не начинаете заново, вы добавляете новую букву X. А как римляне представляют ноль?

Ноль — это уникальное число, не принадлежащее ни к положительному, ни к отрицательному набору чисел. Это был самый последний цифровой символ, который был разработан.Многие древние культуры, такие как шумеры, индийцы, китайцы, египтяне, римляне и греки, разработали различные символы и правила для счета. Но понятие нуля долгое время не появлялось в системах счисления; и даже тогда в римской системе счисления не было символа для нуля. Где-то между шестым и третьим веками до нашей эры ноль появился в шумерской системе счисления, которая была шестидесятеричной (основание 60), как наклонный двойной клин.

Среди древних вавилонских цивилизаций 600 г. до н. Э.c. и раньше, пробел иногда использовался для обозначения «пустого места», однако часто пробелы не использовались. Следовательно, с использованием аккадских символов и вавилонского основания из шестидесяти, числа 1, 60, 3600 и 216000 были написаны одним и тем же символом. Несмотря на потенциальную путаницу, этот метод, по-видимому, был приемлем в течение нескольких столетий. Около 300 г. до н. Э. вавилоняне изобрели специальный знак, который служил заполнителем там, где отсутствовала цифра. Однако этот символ, по-видимому, использовался только для промежуточных пустых позиций, поэтому вавилоняне так и не достигли абсолютной позиционной системы счисления.

Считается, что первый символ нуля появился в четвертом веке до нашей эры. неизвестного индийского математика. Желая записать более постоянный ответ со своей счетной доски, вышитой бисером, он использовал простую точку, называемую шунья, для обозначения столбцов, в которых не было бусинок. Бусины были обозначениями чисел, а точки — заполнителями. В рекламе. 150 астроном Птолемей начал использовать омикрон (первая буква греческого слова, означающая «ничто») вместо нашего нуля в качестве заполнителя.Однако нет никаких свидетельств того, что он рассматривал этот символ как число, которое можно было бы использовать в вычислениях. Омикрон — 15-я буква греческого алфавита. В греческой системе счисления оно имеет значение 70. Оно редко используется в математике, поскольку неотличимо от буквы «о» и легко спутывается с нулем.

Гениальность нашей системы счисления заключается в сочетании характеристик разряда и числового заполнителя, то есть символа числа ноль.Хотя ноль сначала вводится как число, детей можно попросить выполнить действия по нумерации, которые заставят их думать о нуле как о заполнителе, например, спросить ребенка: «У меня 8 сотен и 3 десятка. Какое у меня число?» Этот шаг поможет ребенку ответить на вопрос: зачем нужен ноль в числе?

Поскольку ноль так важен, мы, как учителя, должны побуждать детей постоянно думать о ноле и укреплять то, что без нуля мы не могли бы считать, определить время, измерить или использовать деньги.Большая часть распорядка дня будет включать в себя ноль, который необходимо начинать с первого дня в школе и продолжать в течение всего учебного года. Если ребенок выучит это однажды, он забудет, но если мы, как учителя, построим этот нейронный путь с постоянным подкреплением и репрезентацией, у них будет прочная основа.

Эту часть необходимо выполнить с первого дня учебы в школе. Чтобы дети поняли силу нуля, класс необходимо постоянно подкреплять этой темой.Ребенку третьего класса необходимо будет узнать, что ноль не означает «ничего», что он имеет большую ценность в повседневных ситуациях. В зависимости от предварительных знаний в классе, вся единица уроков может длиться от недели до нескольких недель, а затем подкрепление в течение года. Вам как учителю может быть выгодно делать это каждую пятницу в рамках еженедельной процедуры в классе. Раздел состоит из семи отдельных уроков, причем некоторые из уроков состоят из нескольких заданий.

Раздел начнется с уникального знакомства с нулем, так что дети будут заинтригованы и взволнованы обучением. Некоторые из других уроков будут включать в себя повторное введение порядка величины с использованием денег, одометр для представления порядка величины, просмотр коротких видеоклипов о значении нуля, создание стихотворений о нуле, чтение литературы об оценке и обнулении, изучение места значение с помощью игры под названием «Переверните», создавая порядок величины с базовыми десятью блоками, используя порядок величины посредством оценки ведущей цифры и сложения внешнего интерфейса.Будет обсуждаться использование нуля в качестве заполнителя. Одна из многих полезных функций Zero — это «заполнитель». Например, в числе 600 ноль сразу справа от 6 сообщает нам, что столбец «десятки» пуст; ноль справа говорит нам, что столбец «единицы» также пуст. Единственный столбец, в котором есть какие-либо значения, — это столбец «сотни». Но если бы мы каким-то образом не указали, что два правых столбца пусты, мы бы написали «600» как «6», а это не то число, которое мы имели в виду.Завершим раздел созданной классом книгой о Зеро.

Литература по математике очень важна для развития данного модуля и для многих уроков является отправной точкой. Первая использованная книга — История счета . Это хорошо изученный и интригующий отчет о том, как эволюционировал счет. Шмандт-Бессерат рассказывает, как паэла, выращивающие фруктовые сады в высокогорье Папуа-Новой Гвинеи, «считают, указывая на части своего тела …. Число 1 называется «левый мизинец», 11 — «левая шея», 16 — «правое ухо» и т. Д. Ведды Шри-Ланки считают без цифр, собирая камешки, чтобы указать их количество. Она также тщательно изучает долгую эволюцию счета посредством абстрактного счета, использования десяти цифр и преимущества арабских цифр по сравнению со старыми системами. Ее строгий научный подход к предмету гарантирует, что читатели никогда больше не будут воспринимать систему счета как должное. Полноцветные иллюстрации делают историю красивой наглядной, а глоссарий дает читателям конкретные определения.Следующая книга — Zero. Это что-то? Ничего? Эта книга ясно показывает, что ноль может быть как «чем-то», так и «ничем», в зависимости от его позиции в числе. Конкретные примеры показывают некоторые способы использования нуля в арифметических вычислениях и его место во всех видах измерений. Иногда читателям не хватает примеров каждой операции, чтобы понять правило, лежащее в основе этого примера. Даны инструкции по изготовлению бумажного одометра. Исторические и анекдотические факты делают книгу еще более интересной.Веселые акварели детей разных национальностей и персонажей-животных иллюстрируют текст и делают материал более привлекательным для юного читателя. Последняя книга, которую мы будем обсуждать, — это оценка . Читатель этой книги научится делать более точные оценки. Он / она может научиться приходить вовремя. Он / она может научиться оставаться в пределах своего пособия. Будут обсуждаться стратегии оценки, чтобы показать детям, как легко сделать точную оценку, а не угадывать количество или размер объекта.

Математическая цель этого блока — понимание оценки ведущей цифры. Вы можете подумать, зачем выбирать этот метод? Ну это просто. В моем штате третьеклассники впервые сдают государственный стандартизированный оценочный тест (PSSA). В ходе своего исследования выяснилось, что третьеклассник вообще не умеет пользоваться калькулятором. Если я смогу дать им стратегию, позволяющую исключить несколько вариантов ответов с множественным выбором, я хорошо им послужил и выполнил свою работу. Несколько дополнительных баллов, которые это дает ребенку, могут стать разницей между продвинутым учеником и профессионалом.

Круглогодичная деятельность

Во время утреннего сообщения я прошу детей писать в свои дневники. В рамках этого упражнения мы включим подсчет дней в школе с помощью соломинок. Каждый день в школе одну соломинку кладут в чашку. Чтобы начать разработку порядка величины на 10-й день, мы свяжем 10 соломинок вместе и поместим их в чашку для десятков. Класс должен продолжать объединять наборы из 10, пока мы не достигнем 100, и, естественно, объединить все 100 вместе.

Чтобы помочь детям понять, что ноль действительно важен, им нужно будет связать то, что они делают в классе, с важностью нуля. В нематематическом смысле мой класс поймет, что всякий раз, когда они делают что-то экстраординарное, они могут гордиться собой. Они смогут показать всему классу, что они важны. У нас будет знак Super Zero the Hero на полу, который будет огромным нулем, застрявшим на полу. Любой, кто добивается победы в учебе в течение учебного года, заслуживает победного танца, чтобы показать хорошо выполненную работу героя.Как и футболист, который только что выбежал на приземление, он заслуживает празднования. Однако это упражнение необходимо выполнять так, чтобы учитель решил, кто заслуживает победного танца. Связь будет в том, что без нуля математика будет очень сложной, а без успеха обучение будет очень сложным.

Каждый урок математики начинается с повторения Учителя: «Мы что, ничто?» Студенты: «Нет! Мы — ноль». Учитель: «Мы что-то?» Студенты: «Да! Мы — ноль». Учитель: «А мы маленькие?» Студенты: «Нет! Мы — ноль?» Учитель: «Мы важны?» Студенты: «Да! Мы — ноль.»Это просто забавное взаимодействие, которое укрепит ноль и увлечет детей математикой.

Мероприятие в течение последнего года будет заключаться в еженедельном посещении компьютерной лаборатории, чтобы практиковать то, что мы узнали. Пожалуйста, обратитесь к рекомендуемым интерактивным веб-сайтам в приложении, чтобы выбрать игры и занятия, доступные для всех учителей.

Урок 1

Рассказ: «Сегодняшний урок — ваш самый первый урок математики в третьем классе.Сколько раз вы до этого ходили на урок математики в третьем классе? »Ответ должен быть« ноль ».« Я так и думал! »(Намекая на урок)« Мы собираемся сыграть в игру под названием «Угадай мой номер». Я думаю о числе не больше 10. Я хотел бы, чтобы каждый взял это число и поднял вверх столько пальцев ». Когда дети это сделают, объявите, у скольких детей есть правильный ответ. (ноль) Дети затем нужно потратить несколько минут, чтобы осмотреть комнату, чтобы увидеть, какие числа были представлены (если у трех детей ноль, и я сказал, что три, они смотрят, какое число имеет три.) Если никто не угадает ноль, вы можете сказать: нужное количество людей угадали верное число. Не сказав детям, которые были правы, попросите их изменить свое число на число, которое, как они теперь думают, оно есть. Снова посчитайте, у скольких детей оно правильное, пусть они мысленно вычисляют правильное число. В конце концов, у всех учеников должно быть ноль пальцев в воздухе. Зеро можно представить либо без поднятых рук, либо с поднятым вверх кулаком. Идеальным сценарием было бы, чтобы ребенок, который никогда не отвечает на вопросы, первым правильно набирает числа, потому что он, вероятно, не будет поднимать пальцы.Обсудите их предварительное знание нуля, включая следующие наводящие вопросы. «Ноль важен?» «Всегда ли был ноль?» «Как вы думаете, почему мы не считаем с нуля?» «Когда мы используем ноль?» После обсуждения посмотрите видео «Zero my Hero» из Schoolhouse Rock. После просмотра видео спросите детей, есть ли у детей еще мысли, которые они хотели бы добавить о нуле. Прочтите книгу History of Counting частично или полностью в зависимости от предварительных знаний.

Практическое задание : Попросите одного ребенка подойти к доске и написать цифру 1, и вручить ему / ей пенни «Я дал вам один пенни, как вы к этому относитесь?» Что вы можете сделать с одним пенни? » Попросите другого ребенка написать ноль справа от единицы.«Какое число у нас сейчас? 10, верно! Я дам вам 10 пенни. Вы хотите столько пенсов? Что вы можете сделать с таким количеством пенсов? Продолжайте с 100. Проделайте то же самое. И да. Дайте ребенку мешок 100 пенни или 2 рулона пенни. Я бы остановился на этом месте, если только вы не находитесь в районе, который платит вам столько, сколько вы стоите! Чтобы избежать зависти среди других студентов, можно использовать пластиковые или бумажные пенни, но может не иметь эффект, который я ищу.

Задача дня : Вместе с партнером опишите, что будет дальше.Вы можете нарисовать картинку, составить диаграмму или показать цифрами, но не забудьте описать это словами. Дайте им время поработать вместе, оставив достаточно времени для обсуждения около 1000.

Урок 2

Просмотрите пенни-задание из предыдущего урока. Объясните деятельность в коридоре: используя точки и точечные бумажные массивы, мы изобразим до 1 миллиона точек. Эта активность будет увеличиваться путем умножения предыдущей суммы на 10 или прибавления нуля к предыдущему числу.В группе начните с нескольких первых чисел, которые будут представлены, и повесьте их на стене в классе. (1, 10, 100). По мере продолжения обсуждения напоминайте учащимся, что каждый раз, когда добавляется еще один ноль, он увеличивается на порядок. С каждым числом отображаем массив точек. С 1000 спросите, может ли кто-нибудь угадать, какие массивы мы могли бы использовать для представления 1000. Помните, что вы можете использовать 10 из 100 массивов, чтобы равняться 1000, и это то, какую точку мы хотим найти. ? Если вы вставите эти 10 массивов на бумагу и скопируете их, тогда будет легко представить 10 000 и так далее.

Практическое занятие: Как только все поймут, как создавать массивы, запишите следующие несколько чисел, которые будут следовать в шаблоне. Пусть каждая группа выберет число для создания и предоставит им достаточно массивов точек, чтобы получить свое число. Это занятие может показаться сложной утомительной проблемой. Если вы не дойдете до 1 миллиона, в этом вся прелесть. Урок разработан для того, чтобы дети узнали, насколько на самом деле велик миллион. Для простоты изготовления в книге Building on Numbers, которую вы знаете, , есть демонстрационные листы с 5 000 и 6 300 точками, которые можно использовать как угодно.Вы можете найти эти страницы на страницах 197 и 198 этой книги над текстом. Затем дисплей можно разместить в коридоре как классный проект. В заключение урока прочтите книгу «Миллион точек».

Урок 3

В начале урока прочтите студенческую книгу Zero. Это что-то? Это ничего? Книга представляет собой введение в использование нуля. Есть занятия, стихи и загадки про ноль. Он показывает округление, ноль в качестве заполнителя и подсчет.Это интересная книга.

Практическое занятие : После чтения попросите каждого ребенка сделать одометр. Инструкции начинаются на странице 15. Не забудьте указать ноль. Когда одометры закончены, дайте ученикам несколько чисел, которые они должны создать с помощью одометра. Им нужно написать число на листе бумаги, написать сколько тысяч, сотен, десятков и единиц. Продолжайте, пока класс не усвоит упражнение. Следующий шаг — использовать колоду карточек с числами и перевернуть 4 числа, чтобы дети составили наибольшее и наименьшее, используя только каждую цифру на карточках один раз.Им нужно написать числа на бумаге и при необходимости использовать одометр. Последним мероприятием в течение дня было бы собрать их парами и сыграть « больше, чем меньше» g ame. Каждый ребенок будет создавать числа, используя разные числа в каждом значении разряда (не дает им постоянно использовать 9999 и 0000). После того, как они создали свое четырехзначное число, они не позволяют другому человеку увидеть это число. Они по очереди (не глядя на количество оппонентов) решают, больше ли их количество, чем их оппонент.Если они верны, они получают одно очко. Затем игра продолжается, и у другого человека есть шанс угадать. Дети должны сами понять, что если первая цифра (тысяча) действительно единственная цифра, на которую им нужно смотреть, если у них разные первые цифры. Если тысячи цифр совпадают, им нужно посмотреть на сотню. Стратегия: Побеждает число, близкое к 9999, если они скажут больше, а число ближе к 0000 обычно будет меньше, чем у оппонентов (пусть они сами это обнаружат).Они должны вести счет и записывать стратегии, которые они могли придумать. Им следует играть в эту игру до тех пор, пока они не поймут систематическую стратегию: поместите наибольшую цифру в разряды тысяч, следующую по величине в разрядах сотен, третью по величине в разрядах десятков и наименьшую в разрядах единиц.

Урок 4

Где ноль падает! Перед открытием урока посмотрите видеоклип «Zero the Hero», обсудите, о чем было видео, а затем начните упражнение.

Практическое занятие : Сделайте карточки с цифрами из дубовой бирки или плотной бумаги, дайте каждому ребенку ноль, а оставшуюся часть числа отложите стороной. Также имейте карточку с десятичной точкой. Учитель должен взять карточку с номером и встать слева от передней части комнаты. Поднимите карточку и скажите: «Я 2 (или какое число вы выбрали), может ли кто-нибудь сделать меня больше?» Выберите кого-нибудь, кто подойдет, встаньте там, где, по их мнению, он должен стоять, и скажите, какой он стал. Также спросите их, во сколько раз оно больше предыдущего? Продолжайте добавлять нули, пока они не перестанут произносить число.Скажите им название этого большего числа. Скажем, они могут продолжать делать это вечно, и что каждый раз, когда они добавляют ноль справа, число становится в десять раз больше. Детям нужно понять, что не нужно много нулей, чтобы получилось действительно большое число.

Задание 2 : Пусть двое детей владеют двумя ненулевыми двузначными числами. Спросите, может ли кто-нибудь показать способ увеличить двузначное число, используя ноль, а затем другой способ (12 может стать 102 или 120). Попросите их объяснить, что означает каждое число и разницу между ними и какое из них больше.Затем спросите, есть ли способ оставить 12 такими же, но по-прежнему использовать ноль (012). Вероятно, это потребует обсуждения, и, в частности, нужно будет поговорить о том, что это означает, или если это что-то значит. Они не привыкли, чтобы слева был ноль. Попросите детей сложить три числа в порядке от меньшего к большему. Это задание должно быть очень тщательным и полным. Это огромная концепция, которую нужно понять. Основная цель этого урока — убедиться, что дети действительно понимают, что ноль в качестве заполнителя может сделать число намного больше.

Задание 3 : Дополнительное задание для продвинутых учащихся: выведите десятичную точку и встаньте рядом с нулем в 012. Попросите детей подумать о том, что только что произошло. Поговорите об этом со своим партнером. Проведите краткое обсуждение, затем они должны написать, нарисовать и объяснить, что произошло с десятичной точкой и нулем. Пример ответа: Когда ноль находится слева и слева от десятичной запятой, он не меняет значение любой другой цифры. Точно так же, если вы добавите ноль справа от десятичной точки, это не изменит значение любой другой цифры.Однако, когда вы вставляете ноль между ненулевыми цифрами, некоторые цифры перемещаются в разные места, и поэтому они получают разные значения.

Урок 5

Напомните ученикам об уроках с монетами и точками. Обсудите с ними, что они помнят. Окончанием обсуждения должна быть связь с порядком величин. Принесите набор базовых 10 блоков. Спросите, может ли ученик показать одну единицу. После этого попросите показать 10 с использованием единичных блоков, а затем изобразить их с помощью стержня.Проделайте то же самое с стержнями, плоскими поверхностями и кубом 1000. Продемонстрируйте, как можно использовать базовые десять блоков для представления чисел, например, 4381 будет иметь 4 куба, 3 квартиры, 8 стержней и 1 единицу. Практикуйтесь с несколькими разными числами, пока все ученики не усвоят концепцию. Обсудите идею о том, что это число представляет собой сумму 4 тысяч, 3 сотен, 8 десятков и 1 единицы.

Задание 1: Дайте каждой группе набор из десяти базовых блоков и указания, которые нужно показать: задача сложения с использованием десятичных блоков и двух однозначных чисел, задача сложения с двумя двузначными числами, двумя трехзначными числами и одним с переноской.Пусть каждая группа представит свои данные в картинках и числа в развернутой форме (4000 + 300 + 80 + 1)

Урок 6

Подготовка: Перед занятием убедитесь, что у вас есть карточки с большим числом (дубовая бирка или плотная бумага). На оборотной стороне одного набора карт должны быть цифры 1-9 и ноль. Другой набор карточек должен иметь цифры 1-8 и одну цифру выше на обратной стороне (1 должно иметь 2 на обороте, 2 должно иметь 3 на обороте и т. Д.) Второй набор предназначен для первой цифры любого созданного числа.Первый набор предназначен для следующих цифр любого числа. Вам также нужно будет поставить знак плюса, минуса и равенства.

Задание 1 : Напишите на доске задачу 3 265 + 2 613 или любую подобную задачу. Раздайте одному ребенку карту 3 с 4 на обратной стороне и дайте другому учащемуся соответствующую карту с нулем на обратной стороне и знаком плюс на карте, которую ребенок должен держать. Повторите тот же процесс со вторым числом. Спросите остальных учеников, если 3265 ближе к 3000 или 4000, они должны сказать 3000, чтобы дети перевернули цифры 265, чтобы увидеть нули.Затем попросите детей округлить 2613 до ближайшей тысячи (первая цифра). Это ближе к 2000 или 3000? Это 3000 спросите детей, знают ли они, что нам делать дальше. Они должны ответить: «Переверните 2 на 3 и переверните 613 в ноль». Теперь спросите детей, нужен ли им калькулятор для сложения двух чисел. Их ответ должен быть «нет», потому что легко добавить 2 + 3. Посмотрим, сможет ли кто-нибудь поставить правильный ответ после знака =. Конечно, они должны использовать больше людей. Повторяйте этот процесс до тех пор, пока дети не будут уверены, что понимают округление до первой цифры.Дайте им несколько задач для самостоятельной работы. Как всегда, им нужно записывать проблемы картинками, числами или словами.

Задание 2 : Даже на следующий день начните с обзора, но спросите, насколько все было бы иначе, если бы мы вычитали. Обсудите их идеи и продемонстрируйте любые предложения. Пусть класс попрактикуется в том, чему они научились. Сохраните несколько примеров для книги и повесьте их на стену. Прочтите в классе книгу « Оценка » и обсудите ее.

Урок 7

Поэтический ноль: прочтите несколько стихотворений, написанных о нуле, затем создайте короткие стихотворения. Включите выполнение Number Stomp. Сделайте учебник на тему « The Amazing Zero Starring

в: «Различная ценность, оценка и порядок величины». Может включать картинки, стихи, рассказы, математические задачи и Историю нуля. Обложка должна быть создана и ламинирована, а страницы могут быть переплетены на переплетной машине.

Кэткарт, Джордж и Потье, Ивонн.1997. Изучение математики в начальной и средней школе . второе изд. Нью-Джерси: Прентис-Холл. Оригинальное издание, 2000 г. Эта книга об изучении математики — о детях, изучающих математику. Речь также идет о том, что учителя создают среду обучения, которая поддерживает и поощряет детей к взаимопониманию, установлению связей, рассуждению и решению проблем.

Ифрах, Джордж. 1985. От единицы к нулю, Всеобщая история чисел . Нью-Йорк: Viking Penguin Inc.Эта уникально разносторонняя и оригинальная книга описывается автором как «археология чисел». Книга сделана яркой и ощутимой благодаря сотням иллюстраций.

Каплан, Роберт. 1999. Ничто, естественная история нуля . Нью-Йорк: Оксфорд. Эта история нуля раскрывает истину о природе не только математики, но и самой человеческой мысли. Прелесть математики в том, что, хотя мы ее изобретаем, кажется, что мы переписываем то, что уже существует.

Кацман, Памела и МакКлис, Джеки. Достаточно близкая встреча . США: Дейл Сеймур, 1983. Это рабочая тетрадь с упражнениями для оценки. Эта книга была бы идеальной для студентов старших классов или в качестве дополнения к вышеупомянутым урокам.

Рассел, Сьюзен и Тирни, Корнелия. Основываясь на числах, которые вы знаете . Уайт-Плейнс, Нью-Йорк: Дейл Сеймур, 1998. Учебная программа «Исследования» воплощает новый подход, основанный на многолетних исследованиях того, как дети изучают математику.Уровень Eacfh состоит из набора отдельных модулей. Это 5-й класс.

Рассел, Сьюзан и Рассел, Корнелия. Контрольные точки измерений . Уайт-Плейнс, Нью-Йорк: Дейл Сеймур. 1998. его учебная программа по исследованиям воплощает новый подход, основанный на многолетних исследованиях того, как дети изучают математику. Уровень Eacfh состоит из набора отдельных модулей. Это тоже 5 класс.

Сейф, Чарльз. Зеро, Биография опасной идеи .Нью-Йорк: Penguin Group. 2000. Эта книга следует за числом от его рождения как восточной философской концепции до его борьбы за признание в Европе и его апофеоза как тайны черной дыры.

Threewit Fran. Назначение оценки . Сан-Леандро, Калифорния: Ваттен / По. 1992. В рамках этого учебного курса учащийся начальной школы совершает оценочную поездку с использованием паспорта. В комплект поставки входят планы уроков, рабочие листы и инструкции.

Вайнштейн, Лаверенс и Адамс, Джон Х. Предположения . Princeton N.J. Princeton University Press. 2008. Эта книга наполнена оценочными задачами, аналогичными задачам Ферми. Уровень сложности начинается легко и продолжает расти с каждой проблемой.

Дерево, стружка. Мерил, дети в классе 4-14 лет . MA: Северо-восточный фонд для детей, 1997. Ресурс для учителей и родителей детей в возрасте от 4 до 14 лет. Книга содержит краткие описания универсальных характеристик детей разного возраста.. Практический ресурс по развитию ребенка.

Бриммер, Ларри Дейн. Обезьянья математика . CT: Детская пресса. 2007. Простая счетная книга с использованием базовой оценки.

Клементс, Эндрю и Рид, Майк. Миллион точек . Нью-Йорк: Детское издательство Саймона и Шустера. 2002. Книжка с картинками показывает ребенку, как будут выглядеть миллионы точек.

Франко, Бетси. Время оценить . Манкато, Миннесота: Capstone Press.2002.

Франко, Бетси. Считая наш путь к сотому дню . Нью-Йорк; Маргарет МакЭлдерри. 2004. Стихи и стишки про 100 ^-й день школы

Хобан, Тана. Давайте посчитаем. Нью-Йорк: Уильям Морроу и компания. Inc. 1999. Счетная книга, в которой обсуждается происхождение чисел.

Джонсон, Стивен Т. Город в цифрах. Нью-Йорк: Книги Пингвинов. 1998. Книжка с картинками, показывающая, как числа представлены в повседневных ситуациях

Линн, Чарльз Ф. Оценка . Нью-Йорк: Компания Томаса Ю. Кроуэлла. 1970. В этой книге рассказывается о различных стратегиях оценки. Это также показывает, насколько важно уметь оценивать.

Мерфи, Стюарт Дж. Бетча . Нью-Йорк: издательство HarperCollins. 1997. Рассказ о победе в конкурсе оцениванием.

Мерфи, Стюарт Дж. 100 дней прохлады . Харпер Трофи. 2004. Рассказ о 100 днях школы и о детях, о которых говорится в рассказе, которые были крутыми все 100 дней.

Шмандт-Бессера, Дениз. История счета. New York: Harper Publisher 1999. Детская историческая книга о счетах и ​​числах.

Шварц, Дэвид. За миллионами . Двойной день. 1999. Рассказ о числах больше миллиона и о том, как они выглядят. Показаны научные обозначения и степени десяти. Обсужден гугол (100 нулей)

Заславский, Клавдия. Ноль.Это что-то? Это ничего? Нью-Йорк: Франклин Уоттс. 1989. Загадки, стихи и занятия о числах.

Интернет-ресурсы

Макфи, Исаак М. http://math.suite101.com/article.cfm/the_number_zero Число ноль История формулирования ничего

Ladhani, Рафик. «Нуль.» [Доступно в Интернете] Доступно по адресу http://www.bookrags.com/research/zero-mmat-04/. [Цитировано 8 июля 2008 г.]

О’Коннор Дж. Дж. И Робертсон Е. Ф. http: // www-history.mcs.st-andrews.ac.uk/HistTopics/Zero.html История нуля

http://www.rif.org/assets/Documents/readingplanet/ReadAloud_Stories/zero_the_hero.html: Анимационный рассказ «Обнуление героя», сделанный по мультфильму Джейн Лестер

http://www.kinderhouse.net/zero_the_hero.htm: Еще одна история Zero the Hero

http://www.songsforteaching.com/jennyfixmanedutunes/zerothehero.htm: песня и текст еще одной песни Zero the Hero.

http://www.drjean.org/html/monthly_act/act_2006/01_Jan/pg03d.html: топчет числа Д-р Жан

http://www.shodor.org/interactivate/activities/Estimator/?version=1.6.0-oem&browser=MSIE&vendor=Sun_Microsystems_Inc. Это отличное занятие для демонстрации стратегий оценки длины, площади и плотности населения. Он учит ребенка делать обоснованные оценки, а не гадать.

http: // education.jlab.org/placevalue/ Цель игры «Расстановка ценностей» состоит в том, чтобы создать максимально возможное число из цифр, которые дает вам компьютер. К сожалению, компьютер будет выдавать вам каждую цифру по одной, и вы не будете знать, каким будет следующее число. Вам не разрешается переставлять какие-либо цифры, которые вы уже разместили, поэтому хорошо подумайте, прежде чем закрепить номер на месте! Удачи!

http://arcytech.org/java/b10blocks/instructions.html Этот сайт дает маленьким детям первое введение в использование базовых 10 блоков.

http://nlvm.usu.edu/en/nav/frames_asid_154_g_1_t_1.html Этот сайт использует базовые десять блоков до 1000 и разрабатывает дополнительные проблемы с блоками.

http://www.funbrain.com/guess2/index.html FunBrain Magician предложит вам математическую задачу со словами. Если ваш ответ слишком высокий или слишком низкий, FunBrain сообщит вам об этом. Постарайтесь решить проблемы со словами с минимальным количеством попыток.

http://www.aaamath.com/plc31e-placevalue-w2n.html побуждает ребенка менять числа, написанные словами, на число, которое он представляет. Следит за правильными ответами. Это будет хорошей оценкой для завершения единицы по числовой стоимости.

http://www.aaamath.com/B/g5_31_x1.htm Этот сайт похож на предыдущий, но имеет много скрытых нулей в написании чисел.

http://www.aplusmath.com/Flashcards/rounding.html Этот сайт заставляет ребенка действительно следовать письменным указаниям.Каждая флэш-карта просит их округлить до разного разряда. После 10 карточек ребенку дается процент правильных ответов

http://www.oswego.org/ocsd-web/games/Estimate/estimate.html Это числовая линия, оценивающая деятельность, идеально подходящую для всего класса, с использованием грифелей / мелка для всех участвующих детей. Для всех уровней квалификации можно использовать разные уровни оценки.

http://pbskids.org/curiousgeorge/games/how_tall/how_tall.html Важной частью подготовки к школе является приучение детей к измерению и оценке с использованием стандартных и нестандартных единиц измерения. Например, дети учатся измерять длину комнаты по стопам. В этой интерактивной игре детям предлагается оценить высоту объекта, используя различные нестандартные единицы измерения — шины, пончики и монеты.

http://pbskids.org/curiousgeorge/games/count_your_chickens/count_your_chickens.html

Цель этой игры — помочь детям отточить навыки счета и оценки.Попутно их знакомят со сравнительным языком «больше» и «меньше», поскольку они помогают Джорджу поймать непослушных (но очаровательных) цыпочек. В этой игре есть три разных уровня, но сложность задач на каждом уровне определяется текущими способностями вашего ребенка.

Стандарты оценки третьего класса

Категория 2.2.3 : Вычисление и оценка

2.2.3.A Применяйте сложение и вычитание в повседневных ситуациях, используя конкретные предметы.

2.2.3.E Используйте навыки оценки, чтобы делать выводы.

2.2.3.F Определить обоснованность рассчитанных ответов.

1. Этот абзац был взят из PowerPoint, написанного доктором Робином Иттигсоном математическим руководителем государственных школ Питтсбурга для семинара по написанию учебных программ

2. (Изучение математики pg112)

3. (Зельман, Белл)

4.(TERC, Tierney)

5. http://dimacs.rutgers.edu/nj_math_coalition/framework/ch20/ch20_03-04.html

30+ лучших занятий и игр для обучения распознаванию чисел!

Эти удивительные идеи распознавания чисел для Teaching Number Recognition идеально подходят для детей детского сада или дошкольного возраста. Опробованные и проверенные игры и упражнения с распознаванием чисел для изучения названий чисел, цифр и счета.

Обучение дошкольников по распознаванию чисел

Вот сборник практических занятий по обучению распознаванию чисел дошкольников, детсадовцев и первоклассников.Эти учебные ресурсы и идеи опробованы и проверены в классе, и они обязательно помогут детям узнать все о числах от 0 до 20.

Обучить распознаванию чисел очень легко с помощью этого удобного списка веселых игр по распознаванию чисел, числовых упражнений, печатных форм и рабочих листов для обучения числам.

Наши номера и задания по идентификации номеров гарантированно помогут вашим детям выучить числа, цифры, слова и счет различными способами. От десяти кадров до подстановки в счетчики и отслеживания — есть так много ресурсов для обучения распознаванию чисел.Загрузите их прямо сейчас, если вы хотите, чтобы обучение математике было ЛЕГКОМ!

Связанное сообщение: Дополнительные полезные советы по обучению распознаванию чисел

* этот пост содержит партнерские ссылки. APTR может получать небольшую комиссию за направление ваших покупок без каких-либо дополнительных затрат для вас. Спасибо за поддержку!

Щелкните розовые ссылки, чтобы получить лучшие советы, приемы и печатные формы для обучения распознаванию чисел в нашем блоге! Вам также может быть интересно узнать больше о том, как научить распознавать числа, в других наших публикациях здесь:

Не забудьте добавить эту страницу в закладки и заходите почаще, мы регулярно добавляем новые вещи!

игр на распознавание номеров до 20

Получите КАЖДЫЙ ресурс в нашем магазине всего за 37 австралийских долларов, когда станете VIP-участником! Нажмите на изображение ниже, чтобы узнать больше!

Вы пытаетесь быть лучшим учителем, которым можете быть, но чувствуете себя подавленным и ВЫГОРЯЕТСЯ бесконечным списком дел? Что ж, теперь есть способ найти баланс между работой и личной жизнью и вернуть РАДОСТЬ в преподавание, не делая это ВСЁ самостоятельно! Щелкните изображение сейчас и присоединяйтесь к тысячам учителей, которые победили Burnout и снова нашли РАДОСТЬ в преподавании!

Рулонные и точки для печати чисел для обучения числам

Математика в картонной коробке для яиц для обучения распознаванию чисел

Действия по идентификации номера точного двигателя

Распечатки для распознавания обучающих чисел для пластилина

Занятия по распознаванию обучающих номеров на Хэллоуин

• Игры с числами для печати на Хэллоуин — Попробуйте нашу крафтовую паутину, паучье бинго, карточки с паучьими клипами и игру с паучьими числами, чтобы немного повеселиться и узнать милые числа в этом Хэллоуине!
• Уловите или угостите своих детей обучением с помощью этих жутких ковриков для распознавания чисел Хэллоуина — Тыквы 0-20
• Дополнение на тему Apple из Море знаний — Использование «Десяти красных яблок» Пэта Хатчинса для обучения дополнению

Обучающие числа со снеговиками Тематические игры с числами

Дополнительные упражнения для обучения числовым именам

Продукты A Plus для обучения распознаванию чисел

Бесплатная распечатка рабочих листов для распознавания номеров

Не пропустите !!! Подпишитесь на наш блог, чтобы получить следующую идею ресурсов и бесплатную распечатку, доставленную на вашу электронную почту !!!

Плакаты для разговоров по бесплатному номеру

Обучающее чувство числа — это своего рода большое дело в ранние годы.У наших друзей-блоггеров в Sea of ​​Knowledge также есть список некоторых невероятных практических занятий по математике, которые вы должны увидеть!

Нажмите здесь, чтобы получить больше бесплатных услуг

Деятельность Math Think Board

Придание значимости метательной ценности — Советы Мэнди для учителей

Вы когда-нибудь учили свою метательную единицу стоимости и чувствовали себя неплохо? Ваши дети могут пометить таблицу разрядов, построить числа с базовыми десятью блоками….а затем все резко останавливается при обучении в расширенной форме? Может быть, ваши дети могут писать развернутую форму только тогда, когда они могут «считать нули» для каждого места? Или запутаетесь, когда спросите, каково значение каждой цифры?

Это обычно происходит потому, что дети учатся наизусть наизусть, а не понимают, что на самом деле означает значение каждого места.

Цифры и числа

Во-первых, дети должны понимать разницу между цифрой и числом.Цифры — это символы, используемые для написания чисел. Они могут быть от 0 до 9. Число — это количество чего-либо, записанное цифрами. Например, число 345 записывается с использованием цифр 3, 4 и 5. Это первый урок в моей интерактивной записной книжке с расстановкой значений и многом другом! пакет с интерактивными проектируемыми мини-уроками.

Встраиваемое значение цифры

Как вы можете помочь детям понять значение каждой цифры и значение разряда? Один из способов — как можно раньше внедрить концепцию значения цифры, чтобы дети слышали термин и имели время, чтобы развить понимание значения.Когда я ввожу термин «ценность», я использую базовые десять блоков. Мы обсуждаем ценность или то, что «стоит» каждый блок, как только выйдут базовые десять блоков. Это может помочь детям очень рано столкнуться с этим термином.

С тех пор почти каждая концепция числовой ценности, которую я преподаю, сосредоточена на концепции ценности каждой цифры. Как мне встроить это во все?

Один из приемов состоит в том, чтобы позволить учащимся увидеть, как соотносятся значения каждого места на диаграмме.На одном из моих первых уроков в малых группах ученики на самом деле строят десять блоков, используя единицы, сотню плоских блоков, используя только десятки (я бы тоже делал, но это займет вечность! LOL) и представляют куб тысяч. Вы можете увидеть, как я моделирую это здесь, в этом видео. Это также урок из моего пакета Easy Prep: Place Value.

Советы и уловки для малых математических групп (Place Value Edition)

Готовы ли вы разговаривать небольшими группами? Присоединяйтесь ко мне сегодня вечером, чтобы получить советы и стратегии, чтобы научить ценить ценность в небольших группах.Приготовьте базовые десять блоков! Подпишитесь на мою рассылку, чтобы получать эксклюзивные БЕСПЛАТНЫЕ математические центры, а также будущие советы и обновления! http://eepurl.com/ne8t1 Хотите узнать больше о математическом семинаре? Посмотрите это видео: http://bit.ly/2aYsiKR Мини-уроки по определению ценности http://bit.ly/2aT18nnМетки по определению ценности БЕСПЛАТНО: http://bit.ly/2b5irNU

Автор: Советы Мэнди для учителей в четверг, 18 августа 2016 г.

Важно, чтобы учащиеся видели, как связаны места, потому что им нужно понимать, что числа можно строить по-разному.Для эффективности мы используем несколько сотен, десятков и единиц при торговле. Однако 18 может быть представлено 18 единицами или 1 десяткой и 8 единицами — значение то же самое. В нашем классе мы назвали эти числа «забавными», потому что они выглядели забавно, когда были построены на циновках.

Зачем мне вообще побуждать детей строить числа всеми безумными способами? Разве мы не ХОТИМ, чтобы они эффективно составляли числа, чтобы они могли легко записывать их в стандартной и развернутой формах? Ну и да, и нет.Я действительно хочу, чтобы студенты могли создавать их, чтобы они могли легко писать их в стандартной и развернутой формах.

Однако, если студенты могут мыслить гибко, это сделает более сложные концепции более плавными. Подумайте об этом, когда мы вычитаем с ПЕРЕГРУЗКОЙ. Студенты торгуются на десять и разбивают единицы, чтобы дать им возможность вычесть, верно? А как теперь выглядит это число? Забавный номер! Итак, ЗНАЧЕНИЕ 36 3 десятков и 6 единиц ИЛИ 2 десятков и 16 единиц… которые помогут детям позже при вычитании с группировкой!

Хотите попрактиковаться в «забавных числах»? Посмотрите этот набор «Веселые числа на забавной ферме»! Хотите попробовать это бесплатно? Просто нажмите на картинку ниже, чтобы получить БЕСПЛАТНУЮ!

Ясно как грязь или в этом есть смысл? Хотите больше советов по обучению метательной ценности? Прочтите этот пост! Как научить размещать ценность?

Как научить представления чисел | Разобрался

Многие ученики идут в детский сад, уже умея считать.Они могут произносить числа «один, два, три…» и т. Д. До 10. Но они не всегда понимают, что каждое число, которое они говорят, является числом .

Вдобавок их может сбить с толку тот факт, что одно и то же число может быть представлено по-разному — по названию номера («один») и по его цифре («1»). Путаница в отношении различных представлений чисел может затруднить обучение учащихся сложению и вычитанию.

Практика различных способов показа числа может помочь учащимся понять каждое число как количество.Используя эту стратегию, вы будете использовать явные инструкции для обучения трем различным представлениям чисел 1–10: имени числа, числа и изображения или набора объектов, показывающих количество.

С этими представлениями учащиеся пройдут серию совместных практических занятий. Стратегия заканчивается оценкой обучения, а также вариантами продолжения практики.

Прокрутите вниз, чтобы получить советы по адаптации этой стратегии для дистанционного обучения.

Поделиться Головоломки с числами

• Facebook
• Твиттер
• Pinterest
• Электронное письмо
• Копировать ссылку
• Текстовое сообщение
• Скоро в Google Классе

Задача: Учащиеся идентифицируют число по его письменной цифре, его числовому названию и изображению повторяющихся объектов, показывающих количество.

Уровни оценки (со стандартами):

• K (Common Core K.CC.A.3: Введите числа от 0 до 20. Представьте количество объектов записанными цифрами от 0 до 20, где 0 означает количество объектов, не имеющих.)

• K (Common Core K.CC.B. 4.A: При подсчете объектов произносите числовые имена в стандартном порядке, сопоставляя каждый объект с одним и только одним числовым именем и каждое числовое имя с одним и только одним объектом.)

• K (Common Core K.CC .B.4.B: Помните, что последнее указанное число указывает количество подсчитываемых объектов.Количество объектов одинаково независимо от их расположения или порядка, в котором они были подсчитаны.)

• K (Common Core Math Practice MP2: Размышляйте абстрактно и количественно.)

Лучше всего использовать для обучения с:

Соберите материалы. Распечатайте головоломку с числами для каждой группы от трех до пяти учеников. Подумайте о том, чтобы вырезать кусочки пазла заранее. Вы можете складывать их вместе или собирать в небольшие пакеты. Печать на карточках или ламинирование частей пазла может облегчить учащимся работу с ними.

Подготовьте набор учетных карточек для цифр 1–10. Напишите по одной цифре на каждой карточке. Подготовьте соответствующий набор для имен номеров.

Организуйте небольшие предметы, такие как соломинки, кубики, ластики или счетчики, в группы от 1 до 10. Вы можете сгруппировать объекты в небольшие пластиковые пакеты или чашки, например, пять соломинок в одном пакете или шесть ластиков в чашке.

Совет для учителей: Создайте стену из словесных материалов, чтобы поддержать изучающих английский язык (ELL) и других учащихся, которым нужна визуальная поддержка.Наличие числовых имен рядом с написанными цифрами поможет учащимся выучить их в качестве визуальных слов. Если стена слов не подходит, сделайте таблицу привязок достаточно большой, чтобы ее могли видеть все учащиеся.

1. Разогрейте, просмотрев идентификационный номер. Напишите на доске число от 1 до 10 или укажите на число на стене со словами или в таблице привязок. Произнесите номер вслух. Попросите учащихся повторить номер. Затем попросите учащихся показать и сосчитать количество пальцев, соответствующее количеству.Смоделируйте правильный ответ. Например, для 3 вы можете смоделировать ответ, подняв три пальца и сказав: «Верно. Это 3. » Затем вслух сосчитайте каждый палец. «Раз два три.»

После нескольких раундов объясните ученикам, что есть много способов представления чисел, и использование пальцев — лишь один из них. Спросите: «Как еще мы можем показать число 3?» Получите разные ответы от студентов. Смоделируйте ответы, написав, рисуя и используя предметы в зависимости от того, что говорят учащиеся.

2. Модель, представляющая числа по-разному. Скажите студентам цель сегодняшнего урока. «Сегодня мы познакомимся с тремя различными способами отображения числа. Вы можете использовать цифру. Вы можете использовать имя номера, которое является словом для номера. Или вы можете использовать картинку или набор предметов ». Попросите учащихся повторить концепцию. Скажите: «Итак, вы можете использовать цифры. Скажите со мной цифра . Вы можете использовать числовое имя. Скажи мне номер , имя . Или вы можете использовать картинку или набор предметов.Скажите со мной изображение или набор предметов ».

Покажите им, как выглядят эти изображения. Например, возьмите карту с цифрой 5 и другую с номером «пять». Затем скажите: «Число 5 можно записать как цифру. Но его также можно записать как слово , пять, . Пять. Пять. Пять — это числовое имя. И это может быть показано пятью одними и теми же объектами ». Нарисуйте на доске пять квадратов, считая каждый, пока не дойдете до пяти. «Один два три четыре пять.Пять квадратов. Все они означают одно и то же: 5 (укажите на написанную цифру), 5 (укажите на название числа) и 5 ​​(укажите на квадраты) ».

«Давай попробуем еще раз». Повторите шаги с другим числом из набора 1–10.

Используйте предметы по комнате, чтобы обозначить количество. Вы можете использовать блоки, стойки, мешки с креслами или что-нибудь достаточно большое и яркое, чтобы учащиеся могли видеть их со своих мест.

3. Практикуйте сопоставление цифр и числовых имен с подсчитываемыми объектами. Прежде чем перейти к работе со всеми числами 1–10 и их представлениями, попросите учащихся попрактиковаться с несколькими числами. Поместите набор предметов перед каждой группой учеников, варьируя количество предметов от группы к группе. Этими объектами могут быть счетчики, блоки, соломинки и т. Д. Один учащийся должен отвечать за отображение объектов, чтобы их могли видеть другие участники.

Затем раздайте учащимся четыре каталожные карточки: две с цифрами и две с соответствующими числовыми именами. Например, если перед группой шесть объектов, они могут получить следующие четыре карты: 1, 6, один, шесть.В группе попросите учащихся решить, какие учетные карточки (одно числовое и одно числовое имя) подходят к набору предметов. Пусть студенты обсудят это и придут к соглашению. Свяжитесь с каждой группой и предложите поддержку по мере необходимости. Когда все группы примут решение, предложите им поделиться. Пока они поднимают карточки, предложите им произнести число и произнести по буквам название числа: «s-i-x… шесть».

Перемещайте набор объектов из одной группы в другую и раздайте новый набор карточек каждой группе.Повторите те же действия. После двух раундов, если у каждой группы был успешный матч, переходите к упражнению с числами.

4. Попрактикуйтесь с числами. Раздайте каждой группе набор головоломок с числами (нарезанные заранее или ножницами, если учащиеся делают наборы). Дайте указания: «Теперь мы будем использовать числовые головоломки, чтобы попрактиковаться в различных способах отображения чисел. Разложите все части головоломки на три стопки: цифры, названия чисел и картинки ».

Когда ученики составят три стопки, попросите их перемешать каждую стопку так, чтобы ее части не располагались в определенном порядке.Скажите: «Теперь каждый ученик по очереди выбирает один кусок из стопки цифр. Сообщите членам вашей группы номер, который вы выбрали. Вместе группа будет искать совпадающее имя номера и соответствующую карточку с изображением из двух других стопок, чтобы соответствовать номеру. Продолжайте по очереди складывать части вместе. Когда все части будут объединены в группы по три (цифра, название числа и изображение), поднимите руки, чтобы проверить свою работу ». Смоделируйте, как сделать соответствующий набор, прежде чем ученики начнут.

5. Оценка обучения. Предложите учащимся встретиться с вами один на один за столом с предметами на нем. Дайте каждому учащемуся цифру (учетную карточку или из набора пазлов). Попросите учащихся показать вам соответствующее количество с помощью предметов на столе. Затем попросите их выбрать совпадающее числовое имя из набора учетных карточек или частей головоломки с числами. Попросите учащихся сосчитать предметы и произнести название числа, чтобы показать, что они понимают, что все три представляют собой одно и то же количество.Учащимся, у которых возникают трудности с выполнением этой задачи, следует дать дополнительные инструкции в малых группах, ориентированные на ограниченный набор чисел, например 1–5, а затем 6–10.

6. Продолжение практики. Дайте студентам возможность продолжать практиковаться в представлении чисел. Попробуйте выполнить следующие упражнения для закрепления знаний:

• Сделайте из набора пазлов ожерелья, проделав отверстия с обеих сторон каждого элемента и добавив веревку. Дайте каждому ученику ожерелье.Попросите их встать и найти двух других одноклассников с тем же «номером», но в другой форме.

• Используйте стену слов как способ отметиться с небольшими группами студентов или отдельных лиц. Попросите их определить число, написать название числа и сосчитать предметы.

• Отображение числа в любой форме по вашему выбору. Дайте учащимся время подумать, какое это число. Попросите их найти образцы этого числа в комнате. Затем спросите студентов, где еще они могли бы увидеть формы этого числа в своей жизни.

Учащимся, которые испытывают трудности с математикой в ​​младших классах начальной школы, особенно с пониманием чисел, часто бывает трудно переключаться между различными представлениями чисел. Им сложно понять, что количество такое же. Непосредственно обучая трем представлениям одного и того же количества, вы можете помочь студентам избежать этой путаницы.

Использование физических объектов и изображений для представления величин помогает студентам практиковать и применять концепции стабильного порядка и индивидуальная переписка.Эти концепции необходимы для понимания сложения, вычитания и сравнения величин.

Совместная учебная деятельность в этой стратегии числовой головоломки дает студентам возможность продемонстрировать и передать свое понимание. Совместное обучение особенно полезно для ELL, потому что они могут находить сверстников более доступными и понятными, чем учителя. Студенты, которые могут быть не готовы выполнить задание самостоятельно, также извлекут выгоду из работы со сверстниками. Иногда сверстники могут предлагать корректирующую обратную связь, на которой другие студенты могут учиться.

Предложите способы, которыми семьи могут практиковать представление чисел дома. Например, семьи могут дать учащимся числовое имя, написанное на небольшом листе бумаги, и попросить их найти это количество предметов. Или семьи могут попросить учащихся пометить набор предметов в доме числовым или числовым названием на листе бумаги, чтобы указать количество.

Игра в игры — отличный способ попрактиковаться в числах дома. Настольные игры, такие как Five Little Monkeys и Hi Ho Cherry-O, представляют количество более чем одним способом.

• Сотрудничайте с семьями ваших студентов. Узнайте, какие ресурсы у них есть и что им может понадобиться для поддержки обучения дома.

• Проведите весь класс или небольшие группы учащихся по этапам синхронного онлайн-класса или запишите видео для асинхронного обучения. В любом случае используйте UDL при планировании урока.

• При явном обучении представлений чисел используйте как изображения, так и физические объекты при подсчете каждого числа.Попросите учащихся попрактиковаться в сопоставлении количеств с числами и числовыми именами вместе с вами. Предложите им найти и использовать набор из 10 предметов из своего дома, например цветные карандаши, игровые элементы или монеты.

• Попросите семьи распечатать числа или написать их от руки. Или предложите им использовать онлайн-игру на совпадение, например Представляют числа в пределах 10 .

• Создать онлайн-карточки, чтобы студенты могли практиковать различные представления чисел.Или покажите семьям, как делать карточки из любой бумаги, которая есть у них дома. Карточки можно настроить так, чтобы на одной стороне отображалось имя числа, а на другой — цифры с изображениями объектов (например, точки) для подсчета.

.

No related posts.